numpy矩阵乘法中的multiply,matmul和dot的使用

目录

• 1. multiply（矩阵点乘）
• 2. dot（矩阵叉乘）
• 3. matmul
• 总结

用numpy做矩阵运算时，少不了用到矩阵乘法。本文帮你迅速区分multiply, matmul和dot的区别。

numpy官方文档中的说明：（想深入了解可以一戳）

multiply: https://docs.scipy.org/doc/numpy/reference/generated/numpy.multiply.html

dot: https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html

matmul:https://docs.scipy.org/doc/numpy/reference/generated/numpy.matmul.html

1. multiply（矩阵点乘）

先说说更简单的multiply，如果两个维度完全一样的矩阵用multiply做乘法，那么它们只是进行对应位置元素之间的乘法，得到一个同样维度的矩阵输出。这就是所谓的element-wise product。

import numpy as np
a = np.array([[0,1,2], [1,2,3], [3,4,5]])
b = np.array([[1,1,2], [2,2,1], [1,1,2]])
print(np.multiply(a, b))

输出：

array([[ 0, 1, 4], [ 2, 4, 3], [ 3, 4, 10]])

看这个栗子，应该十分好理解multiply。但是，如果你认为multiply只能对同样维度的矩阵之间相乘，那你就 t/o-o\ simple了。

如果3x3的矩阵和3x1的矩阵用multiply相乘会怎样呢？继续看栗子：

import numpy as np
a = np.array([[0, 1, 2], [1, 2, 3], [3, 4, 5]])
b = np.array([1, 2, 3])
print(np.multiply(a, b))

输出：

array([[ 0,  2,  6],
       [ 1,  4,  9],
       [ 3,  8, 15]])

相当于用b依次乘以a的每一行。记住，multiply是满足交换律的。（a和b互换位置结果不变）

对于3x3的矩阵a，可以用3x1的矩阵与它相乘，也可以用1x3的矩阵与它相乘。还可以用它乘以一个常数：

import numpy as np
a = np.array([[0, 1, 2], [1, 2, 3], [3, 4, 5]])
print(np.multiply(a, 3))

相当于a中各个元素乘以3。

2. dot（矩阵叉乘）

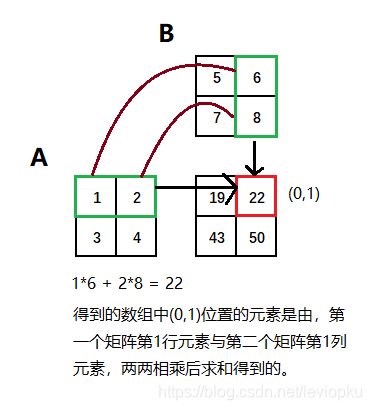
dot就是矩阵叉乘，MxN矩阵乘以NxC矩阵会得到一个MxC的矩阵。对于2D情况下的dot，等同于matmul，也等同于运算符@。

用一张图很好解释：

>>> a = [[1, 0], [0, 1]]
>>> b = [[4, 1], [2, 2]]
>>> np.dot(a, b)
array([[4, 1],
       [2, 2]])
>>> a@b
array([[4, 1],
       [2, 2]])

3. matmul

matmul不支持标量乘法，在2D矩阵乘法中，其效果与dot一样。

在N维矩阵乘法中(N>=3)，体现出与dot不一样的算法。

>>> a = np.ones([9, 5, 7, 4])
>>> c = np.ones([9, 5, 4, 3])
>>> np.dot(a, c).shape
(9, 5, 7, 9, 5, 3)
>>> np.matmul(a, c).shape
(9, 5, 7, 3)
>>> # n is 7, k is 4, m is 3

总结

1. dot和multiply对于标量相乘，效果一样，而matmul不支持标量相乘：

>>>dot(3,3)
>>>9
>>>multiply(3,3)
>>>9
>>>matmul(3,3)
error!

2. 对于2D矩阵相乘，dot和matmul效果一样， 并且这俩都不满足交换律。通常建议优先使用matmul：

from numpy import *
a = arange(9).reshape(3,3)
b = arange(3).reshape(1,3)
 
print(dot(b,a))
print(matmul(b,a))

输出：

[[15 18 21]]
[[15 18 21]]

到此这篇关于numpy矩阵乘法中的multiply,matmul和dot的使用的文章就介绍到这了,更多相关numpy矩阵乘法中的multiply,matmul和dot内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！