倒置字符串、猜名次、猜凶手、杨辉三角

目录

 

例一：倒置字符串

例二：猜名次

例三：猜凶手

例四：杨辉三角

方法一 

方法二 

---

 

例一：倒置字符串

首先我们先来看一下题目具体要求

再来看一下我们所需要的效果

 这里呢，博主给出两种思路，一种是先将整个字符串逆序，再将单个单词逆序；另一种是先将单个单词厉旭，再将整个字符串逆序

第一种
I like beijing.
.gnijieb ekil I
beijing. like i
第二种
I ekil .gnijieb
beijing. like I

 这里博主采用的是将整个字符串逆序，再将单个单词逆序（采用的是指针，若有宝子不懂得，可以看看博主以前得文章）因为需要逆序整个字符串和每个单词，所以博主在这儿将逆序这个功能单独拿出来，实现函数如下

void jiaohuan(char* p1, char* p2)
{
	while (p1 < p2)//退出循环的条件
	{
		char tmp = *p1;
		*p1 = *p2;
		*p2 = tmp;
		p1++;
		p2--;
	}
}

我们有了这个函数后，后面需要逆序时我们就只需要调用就好了

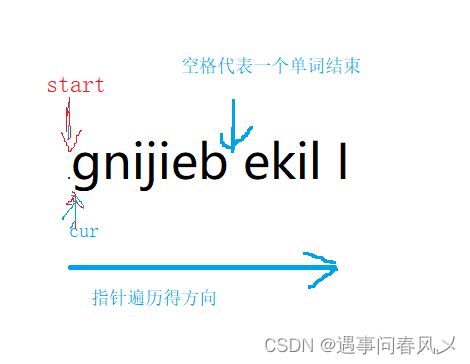
当我们逆序了整个字符串后，逆序每个单词成了我们的难点，首先我们得知道，单词与单词用什么来判断，如何判断结束：单词与单词间我们用空格，结束我们们用‘\0'来判断

这里博主引入两个指针

	char* start = arr;
	char* cur = arr;

 start不用动，cur遍历整个数组，原理如下

其实到这儿我们基本多思考一下就大概可以想到解题代码了，如果没有思路，就浅看一下博主写的吧

while (*cur)
	{
		while (*cur != ' '&&*cur!='\0')//判断跳出循环的条件
		{
			cur++;
		}
		jiaohuan(start, cur - 1);//逆序每一单词
		start = cur + 1;//cur当前指的为空格，所一下一单词得开头需要加一
		if (*cur == ' ')//当有空格时，由于cur此时指得是空格，所以遍历时需要向后进一位
			cur++;      //若没有空格，说明字符串已经遍历完成，不可再加一，否则会造成越界
	}

图解如下

主要功能已完成，我们便可以写出完整代码了，代码如下

#include 

void jiaohuan(char* p1, char* p2)
{
	while (p1 < p2)
	{
		char tmp = *p1;
		*p1 = *p2;
		*p2 = tmp;
		p1++;
		p2--;
	}
}

int main()
{
	char arr[101];
	gets(arr);
	int len = strlen(arr);
	jiaohuan(arr,arr+len-1);
	char* start = arr;
	char* cur = arr;
	while (*cur)
	{
		while (*cur != ' '&&*cur!='\0')//判断跳出循环的条件
		{
			cur++;
		}
		jiaohuan(start, cur - 1);
		start = cur + 1;
		if (*cur == ' ')
			cur++;
	}
	printf("%s", arr);
	return 0;
}

例二：猜名次

题目具体要求如下

考虑到一共五个人，直接模拟推理有些太难，计算机最擅长的遍历此时就会派上用场，将每个人从第1到第5来一遍，则一共会产生5^5种可能性，这个只需要一个5层循环即可搞定。

其实这道题最难的是，如何判断选手那句话为真，其实我们把上述问题给简化一下

 

 我们呢所需要做的只是，对每一位选手说的话只信一半，然后把最后得出名次进行汇总，符合我们的条件就输出

我们发现每一位选手都说了自己与另一名选手的成绩 ，那么我们是否可以把我们循环得到的数字与选手所说的进行判断呢，代码如下

int shuohuang(int m, int n,int x,int y)
//m,n为循环得到选手名词，x,y为选手自己所说名次
{
	if ((m == x && n != y) || (m != x && n == y))
		return 1;
	else return 0;
}

 对每个选手判断后，如果返回值都为1，那么就是我们想要的名次了吗？

这里注意，并不是，博主已经吃过亏了，希望各位宝子可以避免。因为由于循环的原因会导致一些不期望出现的结果出现，因为我并没有查重，所以会出现两个人抢名次的情况，也就是两个人或者更多的人名次相同的情况，例如两个第二，三个第三这样的，所以即使满足了条件，也要查看一下五个人的名次是否重复，这个交给一个函数来执行

int panduan(int a, int b, int c, int d, int e)
{
	if (shuohuang(a, b, 3, 2) && shuohuang(b, e, 2, 4) && shuohuang(c, d, 1, 2) && shuohuang(d, c, 3, 5) && shuohuang(e, a, 4, 1) && (a != b && a != c && a != d && a != e && b != c && b != d && b != e && c != d && c != e && d != e))
		return 1;
	else return 0;
}

到这里我们就完成了一大半了，那么还有一个问题，当你遍历到正确答案，该怎么跳出循环呢，看看博主怎么做的吧

	for (a = 1; a <= 5; a++)
	{
		for (b = 1; b <= 5; b++)
		{
			for (c = 1; c <= 5; c++)
			{
				for (d = 1; d <= 5; d++)
				{
					for (e = 1; e <= 5; e++)
					{
						if (panduan(a, b, c, d, e))//判断成功跳出循环
						{
							ret = 1;
							break;//一个break只跳出一个循环
						}
					}
					if (ret == 1)
						break;
				}
				if (ret == 1)
					break;
			}
			if (ret == 1)
				break;
		}
		if (ret == 1)
			break;
	}

 由于一个break只跳出一个循环，所以这里博主用了多个break；

完整代码如下

int shuohuang(int m, int n,int x,int y)
{
	if ((m == x && n != y) || (m != x && n == y))
		return 1;
	else return 0;
}

int panduan(int a, int b, int c, int d, int e)
{
	if (shuohuang(a, b, 3, 2) && shuohuang(b, e, 2, 4) && shuohuang(c, d, 1, 2) && shuohuang(d, c, 3, 5) && shuohuang(e, a, 4, 1) && (a != b && a != c && a != d && a != e && b != c && b != d && b != e && c != d && c != e && d != e))
		return 1;
	else return 0;
}

int main()
{
	int a = 0;
	int b = 0;
	int c = 0;
	int d = 0;
	int e = 0;
	int ret = 0;
	for (a = 1; a <= 5; a++)
	{
		for (b = 1; b <= 5; b++)
		{
			for (c = 1; c <= 5; c++)
			{
				for (d = 1; d <= 5; d++)
				{
					for (e = 1; e <= 5; e++)
					{
						if (panduan(a, b, c, d, e))
						{
							ret = 1;
							break;
						}
					}
					if (ret == 1)
						break;
				}
				if (ret == 1)
					break;
			}
			if (ret == 1)
				break;
		}
		if (ret == 1)
			break;
	}
	printf("A:%d\nB;%d\nC;%d\nD;%d\nE;%d\n", a, b, c, d, e);
	return 0;
}

例三：猜凶手

题目具体要求如下

本题代码简单，但是呢思维巧妙，相信各位宝子看完代码就可以理解了

#include
int main()
{
   int killer = 0;
   //分别假设凶手是a,b,c,d,看谁是凶手时满足3个人说了真话，一个人说了假话
   for (killer = 'a'; killer <= 'd'; killer++)
   {
    if ((killer != 'a') + (killer == 'c') + (killer == 'd') + (killer != 'd') == 3)
     printf("凶手是：%c", killer);
   }//只需要一个个遍历，满足这四个人中三个人的条件即可判断出来
   return 0;
}

例四：杨辉三角

题目要求为

题目要求了解呢后，我们来了解一下什么叫杨辉三角吧

杨辉三角（也称帕斯卡三角）相信很多人都不陌生，它是一个无限对称的数字金字塔，从顶部的单个1开始，下面一行中的每个数字都是上面两个数字的和。

杨辉三角，是二项式系数在三角形中的一种几何排列，在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲，帕斯卡（1623—-1662）在1654年发现这一规律，所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年，比贾宪迟600年。

方法一 

其实这道题主要是找到规律就好做了，一起来看看博主的代码吧

#include 
int main()
{
	int n = 0;
	int i = 0;
	int arr[1000] = { 0 };
	scanf("%d", &n);
	for (i = 1; i < n; i++)
	{
		arr[0] = 1;
		int j = i-1;
		int x = 0;
		for (; j >0; j--)
		{
			arr[j] = arr[j - 1] + arr[j];
		}
		for (x = 0; x 

 画图解释如下

方法二 

 

void yangHuiTriangle(int n)
{
	int data[30][30] = { 1 }; //第一行直接填好，播下种子

	int i, j;

	for (i = 1; i < n; i++) //从第二行开始填
	{
		data[i][0] = 1; //每行的第一列都没有区别，直接给1，保证不会越界。
		for (j = 1; j <= i; j++) //从第二列开始填
		{
			data[i][j] = data[i - 1][j] + data[i - 1][j - 1]; //递推方程
		}
	}

	for (i = 0; i < n; i++) //填完打印
	{
		for (j = 0; j <= i; j++)
		{
			printf("%d ", data[i][j]);
		}
		putchar('\n');
	}
}

 

以上是博主在学习中遇到的难题，在此分享做题经验，对于这些题目有其他见解的友友，欢迎评论去留言探讨。