基于广义正态分布优化算法的函数寻优算法

一、理论基础

1、广义正态分布优化算法

广义正态分布优化(Generalized normal distribution optimization, GNDO)算法受到正态分布理论的启发。正态分布又称高斯分布，是描述自然现象的重要工具。正态分布可以定义如下：假设一个随机变量$x$服位置参数$\mu$和尺度参数$\delta$的概率分布，其概率密度函数可以表示为：$$f(x)=\frac{1}{\sqrt{2\pi \delta }}\exp \left(-\frac{(x-\mu {)}^2}{2{\delta }^2}\right)\text{\hspace{1em}(1)}$$其中，$x$被称为正态随机变量，这个分布可以称为正态分布，也就是$x\sim N(\mu ,{\delta }^2)$。根据式(1)，正态分布包括两个变量，即位置参数$\mu$和尺度参数$\delta$。位置参数$\mu$和尺度参数$\delta$分别用来表示随机变量的均值和标准差。
GNDO中设计的信息共享策略包括局部开发和全局探索。局部开发基于建立的广义正态分布模型，该模型由当前平均位置和当前最优位置引导；全局探索涉及三个随机选择的个体。这两种学习策略的详细解释如下：

（1）局部开发

局部开发是指在包含所有个体当前位置的搜索空间周围找到更好解决方案的过程。基于个体在种群中的分布与正态分布之间的关系，可以通过以下方法建立优化的广义正态分布模型：$${\mathbf{v}}_i^t={\mu }_i+{\delta }_i\times \eta ,i=1,2,\cdots ,N\text{\hspace{1em}(2)}$$其中，${\mathbf{v}}_i^t$是第$i$个个体在时间$t$的轨迹向量，${\mu }_i$是第$i$个个体的广义平均位置，${\delta }_i$是广义标准差，$\eta$是惩罚因子。${\mu }_i$、${\delta }_i$和$\eta$可以定义为：$${\mu }_i=\frac{1}{3}({\mathbf{x}}_i^t+{\mathbf{x}}_{\text{Best}}^t+\mathbf{M})\text{\hspace{1em}(3)}$$$${\delta }_i=\sqrt{\frac{1}{3}[({\mathbf{x}}_i^t-\mu {)}^2+({\mathbf{x}}_{\text{Best}}^t-\mu {)}^2+(\mathbf{M}-\mu {)}^2]}\text{\hspace{1em}(4)}$$$$\eta =\{\begin{array}{l}\sqrt{-\log ({\lambda }_1)}\times \cos (2\pi {\lambda }_2),\text{if}a\le b\\ \sqrt{-\log ({\lambda }_1)}\times \cos (2\pi {\lambda }_2+\pi ),\text{otherwise}\end{array}\text{\hspace{1em}(5)}$$其中，$a$、$b$、${\lambda }_1$和${\lambda }_2$是介于0和1之间的随机数，${\mathbf{x}}_{\text{Best}}^t$是当前最佳位置，$\mathbf{M}$是当前种群的平均位置。$\mathbf{M}$计算如下：$$\mathbf{M}=\frac{{\sum }_{i=1}^N{\mathbf{x}}_i^t}{N}\text{\hspace{1em}(6)}$$

• 广义平均位置${\mu }_i$。当前最佳个体${\mathbf{x}}_{\text{Best}}^t$包含与全局最优解相关的有用信息。因此，第$i$个个体${\mathbf{x}}_i^t$被拉向当前最佳个体${\mathbf{x}}_{\text{Best}}^t$的方向，后者有更多机会找到更好的解决方案。请注意，当${\mathbf{x}}_{\text{Best}}^t$陷入局部最优时，所有个体仍会朝${\mathbf{x}}_{\text{Best}}^t$的方向移动，这将导致整个种群过早收敛。为了解决这个问题，引入了当前种群的平均位置$\mathbf{M}$，如式(6)所示。种群中的个体可以朝着最佳个体${\mathbf{x}}_{\text{Best}}^t$和平均位置$\mathbf{M}$之间的方向移动。平均位置$\mathbf{M}$在迭代过程中会发生变化，这有利于找到更好的解决方案。因此，在设计的局部开发策略中引入了平均位置$\mathbf{M}$，在一定程度上提高了避免局部最优的机会。
• 广义标准差${\delta }_i$。广义标准差${\delta }_i$用于增强所提出的GNDO的局部搜索能力。基于式(3)和(4)，广义标准差${\delta }_i$可以被视为一个随机序列，在广义平均位置${\mu }_i$周围进行局部搜索。此外，根据式(4)，第$i$个个体${\mathbf{x}}_i^t$的位置和平均位置$\mathbf{M}$与最佳个体${\mathbf{x}}_{\text{Best}}^t$的位置之间的距离越大，生成的随机序列的波动越大。也就是说，当个体${\mathbf{x}}_i^t$的适应度值非常差时，个体找到更好的解决方案的可能性很小。因此，具有强波动的随机序列可以帮助个体寻找更好的解。当个体${\mathbf{x}}_i^t$具有良好的适应值时，个体很有可能在其周围找到更好的解决方案。因此，具有弱波动的随机序列可以帮助个体获得更好的解。
• 惩罚因子$\eta$。在GNDO算法中，惩罚因子$\eta$用于进一步增强生成的广义标准差的随机性。图1显示了由式(5)产生的随机序列。如图1所示，大多数惩罚因子位于-1和1。请注意，生成的广义标准差均为正值。因此，惩罚因子可以增加GNDO的搜索方向，从而提高GNDO的搜索能力。
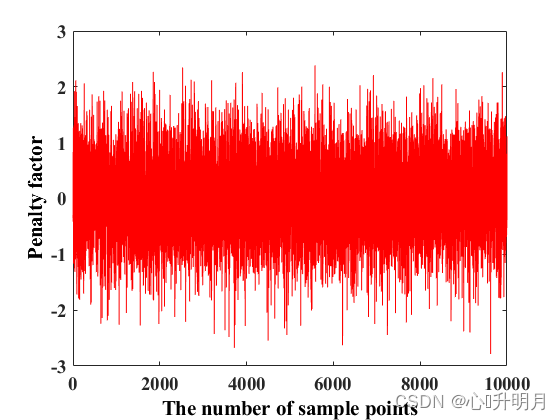
  图1 由式(5)生成的随机序列

（2）全局探索

全局探索是在全局范围内搜索一个有希望的区域。GNDO的全局探索基于三个随机选择的个体，可以表示为：$${\mathbf{v}}_i^t={\mathbf{x}}_i^t+\underset{\text{Local information sharing}}{\beta \times (|{\lambda }_3|\times {\mathbf{v}}_1)}+\underset{\text{Global information sharing}}{(1-\beta )\times (|{\lambda }_4|\times {\mathbf{v}}_2)}\text{\hspace{1em}(7)}$$其中，${\lambda }_3$和${\lambda }_4$是服从标准正态分布的两个随机数，称为调整参数的β是介于0和1之间的随机数，${\mathbf{v}}_1$和${\mathbf{v}}_2$是两个轨迹向量。${\mathbf{v}}_1$和${\mathbf{v}}_2$可通过以下公式计算：$${\mathbf{v}}_1=\{\begin{array}{l}{\mathbf{x}}_i^t-{\mathbf{x}}_{p1}^t,\text{if}f({\mathbf{x}}_i^t)<f({\mathbf{x}}_{p1}^t)\\ {\mathbf{x}}_{p1}^t-{\mathbf{x}}_i^t,\text{otherwise}\end{array}\text{\hspace{1em}(8)}$$$${\mathbf{v}}_2=\{\begin{array}{l}{\mathbf{x}}_{p2}^t-{\mathbf{x}}_{p3}^t,\text{if}f({\mathbf{x}}_{p2}^t)<f({\mathbf{x}}_{p3}^t)\\ {\mathbf{x}}_{p3}^t-{\mathbf{x}}_{p2}^t,\text{otherwise}\end{array}\text{\hspace{1em}(9)}$$其中，$p1$、$p2$和$p3$是从1到$N$中选择的三个随机整数，且满足$p1\ne p2\ne p3$。给定式(8)和式(9)，式(7)右侧的第二项可以称为局部学习项，这意味着个体$p1$与个体$i$共享信息；式(7)右侧的第三项可以称为全局信息共享项，它表示个体$p2$和$p3$向个体$i$提供信息。调整参数$\beta$用于平衡两种信息共享策略。此外，${\lambda }_3$和${\lambda }_4$是标准正态分布的随机数，这可以使GNDO在执行全局搜索的过程中拥有更大的搜索空间。

2、GNDO算法伪代码

GNDO算法伪代码如图2所示。

图2 GNDO算法伪代码

二、仿真实验与结果分析

以常用23个测试函数中的F1、F2(单峰函数/10维)、F9、F10(多峰函数/10维)、F14、F15(固定维度多峰函数/2维、4维)为例，实验设置种群规模为30，最大迭代次数为500，独立运行30次，结果显示如下：

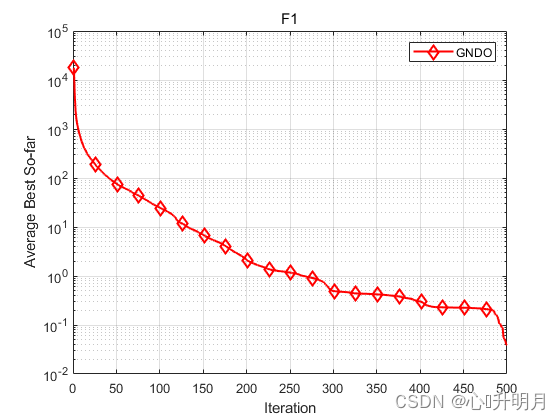
函数：F1
GNDO：最差值: 0.60223, 最优值: 1.0561e-07, 平均值: 0.038551, 标准差: 0.14564
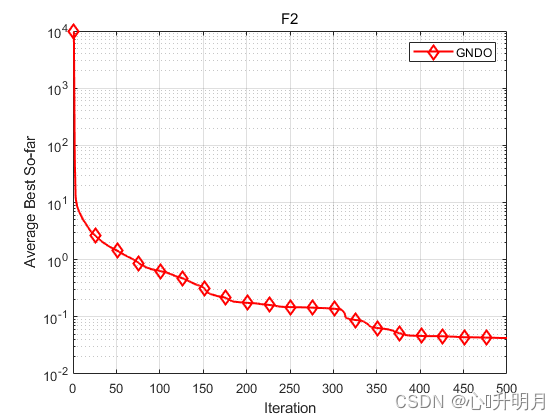
函数：F2
GNDO：最差值: 1.0016, 最优值: 4.1065e-06, 平均值: 0.042532, 标准差: 0.18644
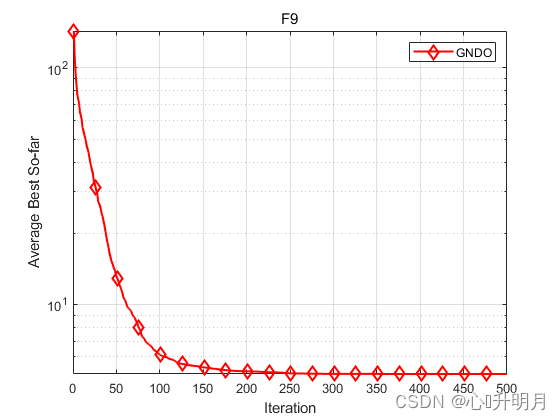
函数：F9
GNDO：最差值: 9.9497, 最优值: 0.99496, 平均值: 5.0774, 标准差: 1.9051
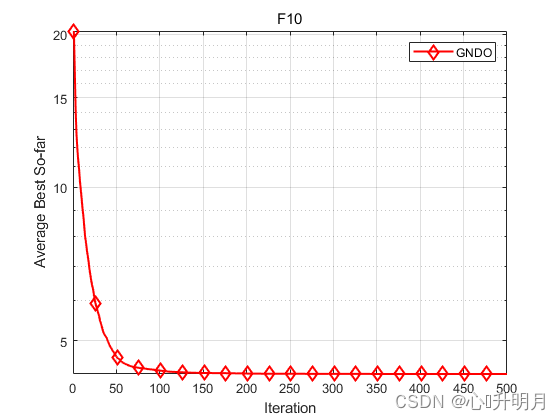
函数：F10
GNDO：最差值: 6.8825, 最优值: 2.3168, 平均值: 4.2981, 标准差: 1.5142
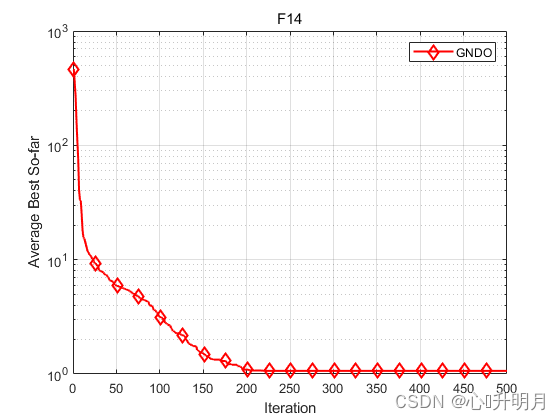
函数：F14
GNDO：最差值: 2.9821, 最优值: 0.998, 平均值: 1.0641, 标准差: 0.36225
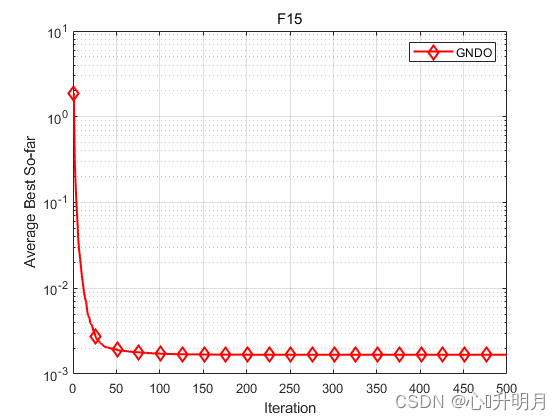
函数：F15
GNDO：最差值: 0.020363, 最优值: 0.00030749, 平均值: 0.001679, 标准差: 0.0050817

实验结果表明：GNDO算法简单有效的算法，无需对初始参数进行任何微调，优化性能良好。

三、参考文献

[1] Yiying Zhang, Zhigang Jin, Seyedali Mirjalili. Generalized normal distribution optimization and its applications in parameter extraction of photovoltaic models[J]. Energy Conversion and Management, 2020, 224: 113301.