最小生成树之普里姆算法

目录

文章目录

前言

一、最小生成树之普里姆算法（Prim）

二、算法实现

1.构造辅助结构体

2.算法实现

总结

---

---

前言

本篇文章主要讲解如何利用图来解决生活中的实际问题，例如：如何用最小的成本构建一个城市的通信网络，或者如何用最小的成本联通周边的城市，下面我将介绍一种算法：最小生成树之普里姆算法。

文章通俗易懂，静下心来都能看得懂！

---

一、最小生成树之普里姆算法（Prim）

普里姆算法是通过寻找最小边的顶点来生成路径最短的树，同时也可以称为“加点法”。

二、算法实现

1.构造辅助结构体

通过构造这个辅助的结构体，来实现寻找图中一组数据的最小的权值，从而达到选择出最小权值的那条边

代码如下（示例）：

typedef struct
{
	VerType adjvex;//最小边在u中的那个顶点
	AreType lowcost;//最小边上的权值
}Close,*closedge;

 至于为什么要在写一个指针变量，这里是为了我后面动态分配内存做准备。（有多少个城市，是不是就要用一个单独的结构体来存储）

图示如下：

 这里只是简单的展示一下分配好的空间

2.算法实现

代码如下（示例）：

void prim(Graph G, closedge &clo)
{
	clo = (closedge)malloc(sizeof(Close) * G.vertex);
	int k = 0;//默认从第一个开始寻找,这里可以进行修改
	for (int i = 0; i < G.vertex; i++)
	{
		if (i != k)
		{
			clo[i].adjvex = G.Ver[k];
			clo[i].lowcost = G.Are[k][i];//初始化顶点集合
		}
	}
	clo[k].lowcost = 0;//这个点找到以后就不再继续寻找

	for (int i = 1; i < G.vertex; i++)
	{
		k = min(clo,G);//寻找当前集合中的最小值
		char u = clo[k].adjvex;//初始化时clo所有顶点都为前一个节点的顶点
		char u1 = G.Ver[k];
		printf("%c%c ", u, u1);//找到之后直接打印出来
		clo[k].lowcost = 0;
		for (int j = 0; j < G.vertex; j++)
		{
			if (G.Are[k][j] < clo[j].lowcost)//这里进行比较，如果权值小那就将顶点和权值交换
			{
				clo[j].adjvex = G.Ver[k];
				clo[j].lowcost = G.Are[k][j];
			}
		}
	}
}

int min(closedge clo, Graph G)//返回最小的权值
{
	int flag = 0;
	int min = MaxInt;
	for (int i = 1; i < G.vertex; i++)
	{
		if (min > clo[i].lowcost && clo[i].lowcost != 0)
		{
			min = clo[i].lowcost;
			flag = i;
		}
	}
	return flag;//用flag返回最小权值所在的数组下标
}

 演示过程：

 这里给了我自己的一组测试用例，&表示两点之间无联系。这里只是替换权值小的顶点，这里第一个最小值找到之后直接打印出来，比如a-c,后面以此类推，下一个节点为f,那就是c-f....

如果已经寻找过了那就将权值赋为0作为标记，下次不再寻找

 至此，普里姆算法就已经全部实现了，还有没写到的也请大家多多包涵！

关于普里姆算法中的图实现，请参照我之前的“图的创建及深度优先搜索”的那篇文章，治理就不再赘述了。

---

总结

这是我数据结构的一些心得，总之也是自己学习过程中的一些体会吧，慢慢的学习总是会有收获的，都是从无到有的，大家一起加油！

这里也附上所有的代码，供大家参考：

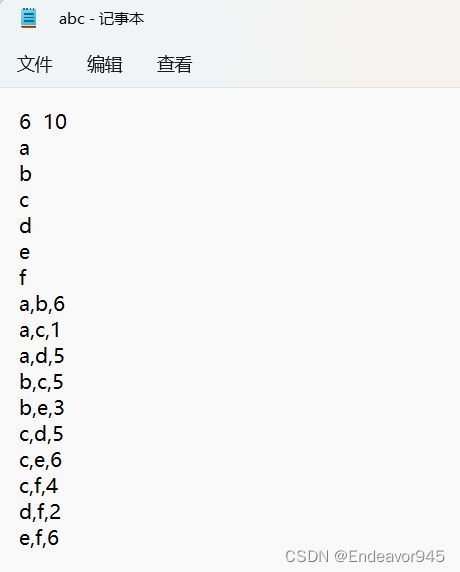
（这里是用文件的方式写入的，自己写一个文本就可以了，这里也放一个我的测试样例截图吧）

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#define MaxInt 32767

typedef char VerType;
typedef int AreType;
typedef struct graph
{
	AreType side;
	AreType vertex;
	VerType* Ver;//顶点
	AreType** Are;
}Graph;

typedef struct
{
	VerType adjvex;//最小边在u中的那个顶点
	AreType lowcost;//最小边上的权值
}Close,*closedge;


int Local(Graph G, char vertex);


void Visit(Graph G)
{
	for (int i = 0; i < G.vertex; i++)
	{
		printf("%-2c", G.Ver[i]);//打印输入的顶点
	}
	printf("\n");
	for (int i = 0; i < G.vertex; i++)
	{
		for (int j = 0; j < G.vertex; j++)
		{
			if (G.Are[i][j] == MaxInt)
				printf("& ");//打印邻接矩阵
			else
				printf("%-2d", G.Are[i][j]);
		}
		printf("\n");
	}
}

void CreatGraph(Graph &G,FILE*fp)
{
	char input;
	G.Ver = (VerType*)malloc(sizeof(VerType) * G.vertex);
	G.Are = (AreType**)malloc(sizeof(AreType*) * G.vertex);

	for (int i = 0; i < G.vertex; i++)
	{
		G.Are[i] = (AreType*)malloc(sizeof(AreType) * G.vertex);
	}

	if ((!G.Ver) && (!G.Are))//分配不成功退出
		return;

	for (int i = 0; i < G.vertex; i++)
	{
		fscanf(fp, "%c\n", &input);
		G.Ver[i] = input;
	}

	for (int i = 0; i < G.vertex; i++)
	{
		for (int j = 0; j < G.vertex; j++)//对邻接矩阵进行初始化
		{
			G.Are[i][j] = MaxInt;
		}
	}
}

void WxW(Graph G,FILE *fp)  //邻接无向网
{
	char b1, b2;
	int n;
	for (int k = 0; k < G.side; k++)
	{
		//printf("请输入第%d条边的两个顶点和权值\n", k + 1);
		//scanf("%c,%c,%d", &b1, &b2, &n);
		//getchar();
		fscanf(fp, "%c,%c,%d\n", &b1, &b2,&n);
		int i = Local(G, b1);
		int j = Local(G, b2);
		G.Are[i][j] = n;
		G.Are[j][i] = n;
	}
}

int Local(Graph G, char vertex)//返回对应点的坐标
{
	for (int i = 0; i < G.vertex; i++)
	{
		if (G.Ver[i] == vertex)//遍历寻找边的位置
		{
			return i;
		}
	}
}


int min(closedge clo, Graph G);

void prim(Graph G, closedge &clo)
{
	clo = (closedge)malloc(sizeof(Close) * G.vertex);
	int k = 0;//默认从第一个开始寻找,这里可以进行修改
	for (int i = 0; i < G.vertex; i++)
	{
		if (i != k)
		{
			clo[i].adjvex = G.Ver[k];
			clo[i].lowcost = G.Are[k][i];//初始化顶点集合
		}
	}
	clo[k].lowcost = 0;//这个点找到以后就不再继续寻找

	for (int i = 1; i < G.vertex; i++)
	{
		k = min(clo,G);//寻找当前集合中的最小值
		char u = clo[k].adjvex;//初始化时clo所有顶点都为前一个节点的顶点
		char u1 = G.Ver[k];
		printf("%c%c ", u, u1);
		clo[k].lowcost = 0;
		for (int j = 0; j < G.vertex; j++)
		{
			if (G.Are[k][j] < clo[j].lowcost)
			{
				clo[j].adjvex = G.Ver[k];
				clo[j].lowcost = G.Are[k][j];
			}
		}
	}
}

int min(closedge clo, Graph G)//返回最小的权值
{
	int flag = 0;
	int min = MaxInt;
	for (int i = 1; i < G.vertex; i++)
	{
		if (min > clo[i].lowcost && clo[i].lowcost != 0)
		{
			min = clo[i].lowcost;
			flag = i;
		}
	}
	return flag;//用flag返回最小权值所在的数组下标
}


int main()
{
	Graph G;
	closedge clo;
	int d, b;
	FILE* fp;
	fp = fopen("abc.txt", "r");//读取名为abc的文本文件 
	if (fp == NULL)
		printf("文件为空！");
	fscanf(fp, "%d %d\n", &d,&b);
	G.vertex = d;
	G.side = b;
	CreatGraph(G,fp);
	WxW(G,fp);
	fclose(fp);
	Visit(G);
	prim(G, clo);
	return 0;
}