word2vec理解归纳(方法概览)
word2vec理解归纳(方法概览)
训练的原因
最早的词向量使用哑编码,也就是one-hot representation,它是以语料库的大小为维度的,对于每一个单词,它的出现体现在它的向量中的一个元素上。但是用这样的向量进行训练和计算,会由于语料的庞大而效率低下。这也是它的问题所在,造成维度灾难。
于是就提出了词的分布式表示即distributed representation。也就是认为规定一个维度 k k k,通过一个权重矩阵 W W W( l e n g t h ( s e n t e n c e ) × K length(sentence) \times K length(sentence)×K)得到 k k k维的稠密向量。
稠密向量的每一个维度上的值,可以理解为一定程度上反映了该词在某个属性上的符合度。
而这样得到的词向量(word embedding)就可以在 k k k 维空间中被其所有的属性限制,并可以用余弦相似度来描述它与其它词向量的相关性,即词的语义逻辑相关性。 ∣ c o s ( θ ) ∣ |cos(\theta)| ∣cos(θ)∣越趋近于1,相似度越大。
这个矩阵 W W W(训练好的)也叫做look up table,即用词的one-hot向量与之相乘得到的向量就是它的词向量。所以问题就归结在了,如何求出这个准确的W。
训练的方法
训练的方法分为Continuous bag-of-words(CBOW)和Skip-gram两个模型,前者是根据作为中心词上下文身份的词来推测中心词,后者方法相反。
此处只拿CBOM分析。
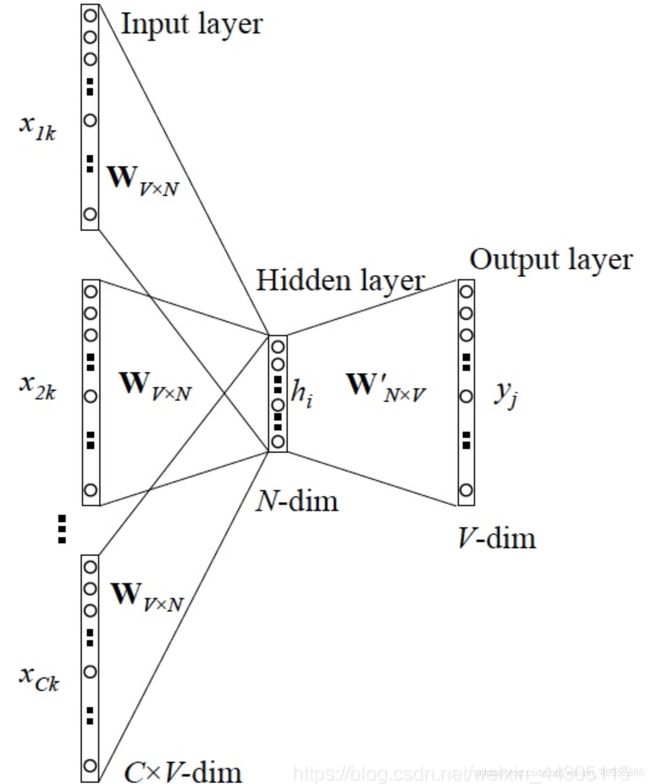
模型如图:
它的目的就是学习 W W W与 W ′ W' W′矩阵,从而通过one-hot词向量 × W \times W ×W得到词向量word embedding。
对于该模型,引入一个实例:['I','like','coding','everyday']
对于Input Layer:
输入的是one-hot类型的词向量(他们的身份是中心词的上下文)
例如例子中:
"I" : [1,0,0,0]
"like" : [0,1,0,0]
"everyday" : [0,0,0,1]
用它们推测:(中心词)
"coding" : [0,0,1,0]
所以输入的one-hot向量,我们把它聚合成一个 C × V C \times V C×V的矩阵,C是被当作上下文的词的个数,V是这个语料库的维度。此处 C = 3 C = 3 C=3,M:
( 1 0 0 0 0 1 0 0 0 0 0 1 ) \begin{pmatrix} 1 & 0 & 0 &0 \\ 0 & 1 &0 &0\\ 0 & 0 &0 &1 \end{pmatrix} ⎝⎛100010000001⎠⎞
初始 W W W(此处W一开始应该是生成的,此处给出一个训练后的):
( 1 1 − 1 2 2 1 3 1 1 0 2 1 ) \begin{pmatrix} 1& 1& -1\\ 2 & 2 & 1\\ 3 & 1 & 1\\ 0 & 2 & 1 \end{pmatrix} ⎝⎜⎜⎛12301212−1111⎠⎟⎟⎞
然后执行一个乘法 M × W M \times W M×W:
( 1 0 0 0 0 1 0 0 0 0 0 1 ) × ( 1 1 − 1 2 2 1 3 1 1 0 2 1 ) = ( 1 1 − 1 2 2 1 0 2 1 ) \begin{pmatrix} 1 & 0 & 0 &0 \\ 0 & 1 &0 &0\\ 0 & 0 &0 &1 \end{pmatrix} \times \begin{pmatrix} 1& 1& -1\\ 2 & 2 & 1\\ 3 & 1 & 1\\ 0 & 2 & 1 \end{pmatrix} = \begin{pmatrix} 1& 1& -1\\ 2& 2&1 \\ 0& 2 & 1 \end{pmatrix} ⎝⎛100010000001⎠⎞×⎝⎜⎜⎛12301212−1111⎠⎟⎟⎞=⎝⎛120122−111⎠⎞
对于hidden layer:
对于矩阵的每一列求了平均值,得到稠密向量。
( 1 + 2 + 0 3 1 + 2 + 2 3 − 1 + 1 + 1 3 ) = ( 1 1.67 0.33 ) \begin{pmatrix} \frac{1 + 2 + 0}{3} & \frac{1+2+2}{3} & \frac{-1+1+1}{3} \end{pmatrix} = \begin{pmatrix} 1 & 1.67 & 0.33 \end{pmatrix} (31+2+031+2+23−1+1+1)=(11.670.33)
对于Output layer:
在将上方的结果乘 W ′ W' W′。要求出一个V维的one-hot向量,再对其 s o f t m a x softmax softmax,得到中心词的概率,最后根据输出概率,采用loss function(交叉熵代价函数),梯度下降算法更新W与W’。
( 1 1.67 0.33 ) × ( 1 − 1 1 0 2 2 2 2 − 1 − 1 2 0 ) = ( 4.01 2.01 5.00 3 , 34 ) \begin{pmatrix} 1 & 1.67 & 0.33 \end{pmatrix} \times \begin{pmatrix} 1& -1 &1 &0 \\ 2& 2& 2& 2\\ -1 & -1 &2 & 0 \end{pmatrix} = \begin{pmatrix} 4.01 & 2.01 & 5.00 & 3,34 \end{pmatrix} (11.670.33)×⎝⎛12−1−12−1122020⎠⎞=(4.012.015.003,34)
s o f t m a x ( ( 4.01 2.01 5.00 3.34 ) ) = ( 0.23 0.03 0.62 0.12 ) softmax(\begin{pmatrix} 4.01 & 2.01 & 5.00 & 3.34 \end{pmatrix}) = \begin{pmatrix} 0.23 & 0.03 & 0.62 & 0.12 \end{pmatrix} softmax((4.012.015.003.34))=(0.230.030.620.12)
0.62即为中心词为“coding”的概率。
对于更深入的探索,后续会继续学习。