机器学习(04)—比较检验
比较检验
- 1. 假设检验(一个数据集一个算法)
- 2. 交叉验证t检验(一个数据集两个算法)
- 3. McNemer检验(一个数据集两个算法)
- 4. Friedmen检验和Nemenyi后续检验(多个数据集多个算法)
机器学习中的性能比较复杂的原因:
- 首先,我们希望比较的是泛化性能,然而通过实验评估获得的只是测试集上的性能,两者对比结果可能未必相同
- 测试集上的性能与测试集本身选择有很大的关系,不同大小的测试集会得到不同的结果,即便是相同大小的测试集,若测试样例不同,测试结果也可能不同
- 很多机器学习算法本身有一定的随机性,即便用相同的参数设置,在同一个测试集多次运行,其 结果也可能不同。
统计假设检验(hypothesis test)为进行学习器性能比较提供了重要依据。基于假设检验结果可推断出,若在测试集上观察到学习器A比B好,则A的泛化性能是否在统计意义上优于B, 以及这个结论的把握有多大。下面将介绍假设检验方法,然后介绍常用的机器学习性能比较方法。为便于讨论,本节默认以错误率为性能度量,用 ϵ \epsilon ϵ表示。
1. 假设检验(一个数据集一个算法)
假设检验中的“假设”是对学习器泛化错误率分布的某种判断或猜想,例如“ ϵ = ϵ 0 \epsilon=\epsilon_0 ϵ=ϵ0”, 现实任务中我们并不知道学习器的泛化错误率,只能获知其测试错误率 ϵ ^ \hat\epsilon ϵ^.泛化错误率与测试错误率未必相同,但直观上,二者接近的可能性应比较大,相差很远的可能性比较小,因此,可根据测试错误率估推出泛化错误率的分布。
泛化错误率为 ϵ \epsilon ϵ的学习器在一个样本上犯错的概率是 ϵ \epsilon ϵ; 测试错误率合意味着在m个测试样本中恰有 ϵ × m \epsilon\times m ϵ×m个被误分类。假定测试样本是从样本总体分布中独立采样而得,那么泛化错误率为é的学习器将其中m’个样本误分类、其余样本全都分类正确的概率是 ( m m ′ ) ϵ m ′ ( 1 − ϵ ) m − m ′ {m \choose m'} \epsilon^{m'}(1-\epsilon)^{m-m'} (m′m)ϵm′(1−ϵ)m−m′; 由此可估算出其恰将éxm个样本误分类的概率如下式所示,这也表达了在包含 m个样本的测试集上、泛化错误率为é的学习器被测得测试错误率为 ϵ ^ \hat\epsilon ϵ^的概率:
P ( ϵ ^ ; ϵ ) = ( m m ′ ) ϵ m ′ ( 1 − ϵ ) m − m ′ (1) P(\hat\epsilon;\epsilon)={m \choose m'} \epsilon^{m'}(1-\epsilon)^{m-m'} \tag1 P(ϵ^;ϵ)=(m′m)ϵm′(1−ϵ)m−m′(1)
给定测试错误率,则解 ∂ P ( ϵ ^ ; ϵ ) / ∂ ϵ = 0 \partial P(\hat\epsilon;\epsilon)/\partial\epsilon=0 ∂P(ϵ^;ϵ)/∂ϵ=0可知, P ( ϵ ^ ; ϵ ) P(\hat\epsilon;\epsilon) P(ϵ^;ϵ)在 ϵ = ϵ ^ \epsilon=\hat\epsilon ϵ=ϵ^时最大, ∣ ϵ − ϵ ^ ∣ |\epsilon-\hat\epsilon| ∣ϵ−ϵ^∣增大时 P ( ϵ ^ ; ϵ ) P(\hat\epsilon;\epsilon) P(ϵ^;ϵ)减小。这符合二项(binomial)分布,如图所示,若 ϵ = 0.3 \epsilon=0. 3 ϵ=0.3, 则10 个样本中测得3个被误分类的概率最大。
二项分布示意图:
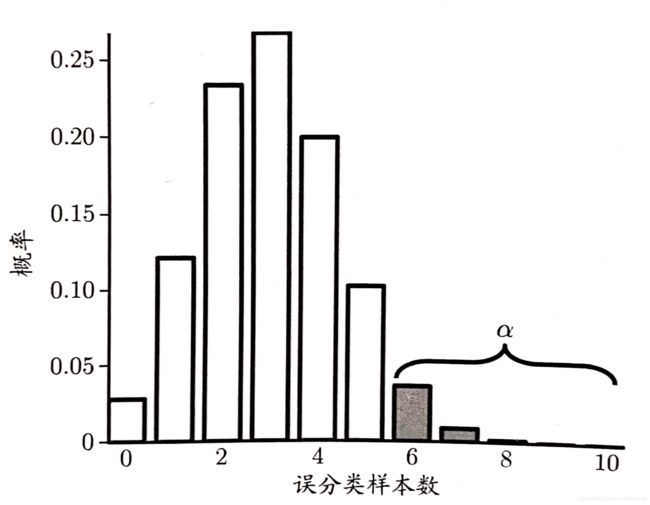
可使用“二项检验”(binomial test)来对“ ϵ ≤ 0.3 \epsilon\le0. 3 ϵ≤0.3”(即“泛化错误率是否不大于0. 3”)这样的假设进行检验。 更一般的,考虑假设“ ϵ ≤ ϵ 0 \epsilon\le\epsilon_0 ϵ≤ϵ0”, 则在 1 − α 1-\alpha 1−α的概率内所能观测到的最大错误率如下式计算。这里 1 − α 1-\alpha 1−α反映了结论的“置信度”(confidence), 直观地来看,相应于图2. 6中非阴影部分的范围
此时若测试错误率 ϵ ^ \hat\epsilon ϵ^小于临界值 ϵ ‾ \overline\epsilon ϵ, 则根据二项检验可得出结论:在 α \alpha α的显著度下,假设“ ϵ ≤ ϵ 0 \epsilon\le\epsilon_0 ϵ≤ϵ0”不能被拒绝,即能以c的置信度认为,学习器的泛化错误率不大于 ϵ 0 \epsilon_0 ϵ0; 否则该假设可被拒绝,即在 α \alpha α的显著度下可认为学习器的泛化错误率大于 ϵ 0 \epsilon_0 ϵ0.
在很多时候并非仅做一次留出法估计,而是通过多次重复留出法或是交叉验证法等进行多次训练/测试,这样会得到多个测试错误率,此时可使用“t检验”(t-test). 假定我们得到了k个测试错误率, ϵ ^ 1 , ϵ ^ 2 , . . . , ϵ ^ k , \hat\epsilon_1,\hat\epsilon_2,...,\hat\epsilon_k, ϵ^1,ϵ^2,...,ϵ^k,, 则平均测试错误率 μ \mu μ和方差 σ 2 \sigma^2 σ2为
μ = 1 k ∑ i − 1 k ϵ ^ i (2) \mu=\frac{1}{k}\sum_{i-1}^k\hat\epsilon_i \tag2 μ=k1i−1∑kϵ^i(2)
σ = 1 k − 1 ∑ i − 1 k ( ϵ ^ i − μ ) 2 (3) \sigma=\frac{1}{k-1}\sum_{i-1}^k(\hat\epsilon_i-\mu)^2 \tag3 σ=k−11i−1∑k(ϵ^i−μ)2(3)
考虑到这k个测试错误率可看作泛化错误率 ϵ 0 \epsilon_0 ϵ0的独立采样,则变量
τ t = k ( μ − ϵ 0 ) σ (4) \tau_t=\frac{\sqrt k(\mu-\epsilon_0)}{\sigma} \tag4 τt=σk(μ−ϵ0)(4)
服从自由度为 k-1的t分布,如图所示。
t分布示意图(k=10)
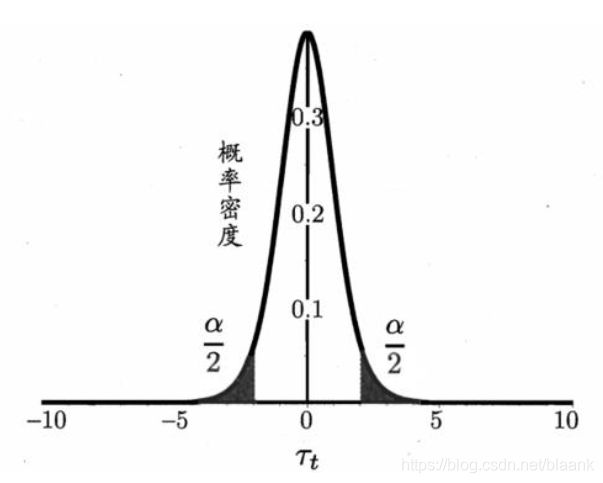
对假设“ μ = ϵ 0 \mu=\epsilon_0 μ=ϵ0”和显著度 α \alpha α, 可计算出当测试错误率均值为 ϵ 0 \epsilon_0 ϵ0时,在 ϵ 0 \epsilon_0 ϵ0概率内能观测到的最大错误率,即临界值。这里考虑双边(two-tailed)假设,如图所示,两边阴影部分各有 α / 2 \alpha/2 α/2的面积;假定阴影部分范围分别为 [ − ∞ , t − α / 2 ] [-\infty,t_{-\alpha/2}] [−∞,t−α/2]和 [ t α / 2 , ∞ ] [t_{\alpha/2,\infty}] [tα/2,∞]. 若平均错误率 μ \mu μ与 ϵ 0 \epsilon_0 ϵ0之差 ∣ μ − ϵ 0 ∣ |\mu-\epsilon_0| ∣μ−ϵ0∣位于临界值范围 [ t − α / 2 , t α / 2 ] [t_{-\alpha/2},t_{\alpha/2}] [t−α/2,tα/2]内,则不能拒绝假设“ μ = ϵ 0 \mu=\epsilon_0 μ=ϵ0”, 即可认为泛化错误率为 ϵ 0 \epsilon_0 ϵ0, 置信度为, 1 − α 1-\alpha 1−α; 否则可拒绝该假设,即在该显著度下可认为泛化错误率与 ϵ 0 \epsilon_0 ϵ0有显著不同。 α \alpha α常用取值有0. 05和0. 1.
上面介绍的两种方法都是对关于单个学习器泛化性能的假设进行检验,而在现实任务中,更多时候需对不同学习器的性能进行比较,下面将介绍适用于此类情况的假设检验方法。
2. 交叉验证t检验(一个数据集两个算法)
对两个学习器A和B, 若我们使用k折交叉验证法得到的测试错误率分别为 ϵ 1 A , ϵ 2 A , . . . , ϵ k A \epsilon_1^A,\epsilon_2^A,...,\epsilon_k^A ϵ1A,ϵ2A,...,ϵkA和 ϵ 1 B , ϵ 2 B , . . . , ϵ k B \epsilon_1^B,\epsilon_2^B,...,\epsilon_k^B ϵ1B,ϵ2B,...,ϵkB, 其中 ϵ i A \epsilon_i^A ϵiA和 ϵ i B \epsilon_i^B ϵiB是在相同的第 i i i折训练/测试集上得到的结果,则可用k折交叉验证“成对t检验”(paired t-tests)来进行比较检验。 这里的基本思想是若两个学习器的性能相同,则它们使用相同的训练/测试集得到的测试错误率应相同,即 ϵ i A = ϵ i B \epsilon_i^A=\epsilon_i^B ϵiA=ϵiB.
具体来说,对k折交叉验证产生的k对测试错误率:先对每对结果求差, Δ i = ϵ i A − ϵ i B \Delta_i=\epsilon_i^A-\epsilon_i^B Δi=ϵiA−ϵiB; 若两个学习器性能相同,则差值均值应为零。因此,可根据差值 Δ 1 , Δ 2 , . . . , Δ k \Delta_1,\Delta_2,...,\Delta_k Δ1,Δ2,...,Δk来对“学习器A与B性能相同”这个假设做t检验,计算出差值的均值 μ \mu μ和方差 σ 2 \sigma^2 σ2, 在显著度 α \alpha α下, 若变量
τ t = k μ σ (5) \tau_t=\frac{\sqrt k\mu}{\sigma} \tag5 τt=σkμ(5)
小于临界值 t α / 2 , k − 1 t_{\alpha/2,k-1} tα/2,k−1, 则假设不能被拒绝,即认为两个学习器的性能没有显著差别;否则可认为两个学习器的性能有显著差别,且平均错误率较小的那个学习器性能较优。这里 t α / 2 , k − 1 t_{\alpha/2,k-1} tα/2,k−1是自由度为k-1的t分布上尾部累积分布为 α / 2 \alpha/2 α/2的临界值。
欲进行有效的假设检验,一个重要前提是测试错误率均为泛化错误率的独立采样。然而,通常情况下由于样本有限,在使用交叉验证等实验估计方法时,不同轮次的训练集会有一定程度的重叠,这就使得测试错误率实际上并不独立,会导致过高估计假设成立的概率。为缓解这一问题,可采用“5x2交叉验证”法。
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.model_selection import cross_val_score
from sklearn import svm
from sklearn import tree
from scipy import stats
from sklearn.linear_model import LogisticRegression
iris = datasets.load_iris()
X = iris.data[:, 2:4]
y = iris.target
for i in range(len(y)):
if y[i] == 0:
y[i] = 2
# X = iris.data[:, :2]
clf_svm = svm.SVC()
scores_svm = cross_val_score(clf_svm, X, y, cv=10)
clf_tree = tree.DecisionTreeClassifier()
scores_tree = cross_val_score(clf_tree, X, y, cv=10)
clf_logic = LogisticRegression()
scores_logic = cross_val_score(clf_logic, X, y, cv=10)
print("logic",scores_logic)
print("tree", scores_tree)
print("svm", scores_svm)
h = .02
clf_svm.fit(X, y)
plt.figure()
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = clf_svm.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors='k')
plt.title('SVM')
plt.show()
clf_logic.fit(X,y)
plt.figure()
ZZ = clf_logic.predict(np.c_[xx.ravel(), yy.ravel()])
ZZ = ZZ.reshape(xx.shape)
plt.pcolormesh(xx, yy, ZZ, cmap=plt.cm.Paired)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors='k')
plt.title('LogisticRegression')
plt.show()
clf_tree.fit(X,y)
plt.figure()
ZZ = clf_tree.predict(np.c_[xx.ravel(), yy.ravel()])
ZZ = ZZ.reshape(xx.shape)
plt.pcolormesh(xx, yy, ZZ, cmap=plt.cm.Paired)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors='k')
plt.title('DTC')
plt.show()
t_score, pvalue = stats.ttest_ind(scores_svm, scores_tree)
print(stats.ttest_ind(scores_svm, scores_tree))
if(pvalue > 0.05 ):
print("SVM与决策树在iris数据集上的学习性能没有显著的差别(95%置信度)")
else:
print("SVM与决策树在iris数据集上的学习性能有显著的差别(95%置信度)")
t_score1,pvalue1 = stats.ttest_ind(scores_svm, scores_logic)
print(stats.ttest_ind(scores_svm, scores_logic))
if(pvalue1 > 0.05 ):
print("SVM与LogisticRegression在iris数据集上的学习性能没有显著的差别(95%置信度)")
else:
print("SVM与LogisticRegression在iris数据集上的学习性能有显著的差别(95%置信度)")
输出:
logic [0.66666667 0.66666667 0.66666667 0.66666667 0.66666667 0.4 0.53333333 0.46666667 0.4 0.66666667]
tree [1. 1. 1. 1. 0.93333333 0.86666667 0.86666667 0.66666667 0.93333333 1. ]
svm [1. 1. 1. 1. 0.93333333 0.86666667 0.86666667 1. 0.93333333 1. ]
Ttest_indResult(statistic=0.8763093567554817, pvalue=0.39240681476176653)
SVM与决策树在iris数据集上的学习性能没有显著的差别(95%置信度)
Ttest_indResult(statistic=9.206330525194632, pvalue=3.138731669274695e-08)
SVM与LogisticRegression在iris数据集上的学习性能有显著的差别(95%置信度)
3. McNemer检验(一个数据集两个算法)
对二分类问题,使用留出法不仅可估计出学习器A和B的测试错误率,还可获得两学习器分类结果的差别,即两者都正确、都错误、一个正确另一个错误的样本数,如“列联表”(contingency table)2. 4 所示。
表2. 4 两学习器分类差别列联表
| 算法B\算法A | 正确 | 错误 |
|---|---|---|
| 正确 | e 00 e_{00} e00 | e 01 e_{01} e01 |
| 错误 | e 10 e_{10} e10 | e 11 e_{11} e11 |
若做的假设是两学习器性能相同,则应有 e 01 = e 10 e_{01}=e_{10} e01=e10, 那么变量 ∣ e 01 = e 10 ∣ |e_{01}=e_{10}| ∣e01=e10∣应当服从正态分布。McNemar 检验考虑变量
τ χ 2 = ( ∣ e 01 − e 10 ∣ − 1 ) 2 e 01 + e 10 (6) \tau_{\chi^2}=\frac{(|e_{01}-e_{10}|-1)^2}{e_{01}+e_{10}} \tag6 τχ2=e01+e10(∣e01−e10∣−1)2(6)
服从自由度为1的 χ 2 \chi^2 χ2分布,即标准正态分布变量的平方。给定显著度 α \alpha α, 当以上变量值小于临界值 χ α 2 \chi^2_\alpha χα2.时,不能拒绝假设,即认为两学习器的性能没有显著差别;否则拒绝假设,即认为两者性能有显著差别,且平均错误率较小的那个学习器性能较优。自由度为1的 χ 2 \chi^2 χ2检验的临界值当 α = 0.05 \alpha=0. 05 α=0.05时为3. 8415, α = 0.1 \alpha=0. 1 α=0.1时为2. 7055.
4. Friedmen检验和Nemenyi后续检验(多个数据集多个算法)
交又验证t检验和McNemar检验都是在一个数据集上比较两个算法的性能,而在很多时候会在一组数据集上对多个算法进行比较,当有多一种做法是在每个数据集上分别列出两两比较的结果,而在算法参与比较时,两两比较时可使用前述方法;另一种方法更为直接,即使用基于算法排序的Friedman检验。
假定用 D 1 D_1 D1、 D 2 D_2 D2、 D 3 D_3 D3和 D 4 D_4 D4四个数据集对算法A、B、C进行比较。首先,使用留出法或交叉验证法得到每个算法在每个数据集上的测试结果,然后在每个数据集上根据测试性能由好到坏排序,并赋予序值1,2,…;若算法的测试性能相同,则平分序值,例如,在 D 1 D_1 D1和 D 3 D_3 D3上,A最好、B其次、C最差,则可列出表2,5,其中最后一行通过而在 D 2 D_2 D2上,A最好、B与C性能相同,…,其中最后一行通过对每一列的序值求平均,得到平均序值。
算法比较序值表:
| 数据集 | 算法A | 算法B | 算法C |
|---|---|---|---|
| D 1 D_1 D1 | 1 | 2 | 3 |
| D 2 D_2 D2 | 1 | 2.5 | 2.5 |
| D 3 D_3 D3 | 1 | 2 | 3 |
| D 4 D_4 D4 | 1 | 2 | 3 |
| 平均序值 | 1 | 2.125 | 2.875 |
然后,使用Friedman检验来判断这些算法是否性能都相同,若相同,则它们的平均序值应当相同,假定在N个数据集上比较k个算法,令 r i r_i ri表示第 i i i个算法的平均序值应当相同,为简化讨论,暂不考虑平分序值的情况,则 r i r_i ri的均值和方差分别为 ( k + 1 ) / 2 (k+1)/2 (k+1)/2和 ( k 2 − 1 ) / 12 (k^2-1)/12 (k2−1)/12变量
τ χ 2 = k − 1 k ⋅ 12 N k 2 − 1 ( r i − k + 1 2 ) = 12 N k ( k + 1 ) ( ∑ i = 1 k r i 2 − k ( k + 1 ) 2 4 ) (7) \tau_{\chi^2}=\frac{k-1}{k}\cdot\frac{12N}{k^2-1}(r_i-\frac{k+1}{2})\\ =\frac{12N}{k(k+1)}(\sum_{i=1}^kr_i^2-\frac{k(k+1)^2}{4}) \tag7 τχ2=kk−1⋅k2−112N(ri−2k+1)=k(k+1)12N(i=1∑kri2−4k(k+1)2)(7)
在k和N都较大时,服从自由度为k-1的 χ 2 \chi^2 χ2分布。
然而,上述这样的“原始Friedman检验”过于保守,现在通常使用变量
τ F = ( N − 1 ) τ χ 2 N ( k − 1 ) − τ χ 2 (8) \tau_F=\frac{(N-1)\tau_{\chi^2}}{N(k-1)-\tau_{\chi^2}} \tag8 τF=N(k−1)−τχ2(N−1)τχ2(8)
其中 τ χ 2 \tau_{\chi^2} τχ2由式(2. 34)得到。 τ F \tau_F τF服从自由度为 k − 1 k-1 k−1和 ( k − 1 ) ( N − 1 ) (k-1)(N-1) (k−1)(N−1)的F分布。
若“所有算法的性能相同”这个假设被拒绝,则说明算法的性能显著不同。这时需进行“后续检验”(post-hoc test)来进一步区分各算法。常用的有Nemenyi后续检验。
Nemenyi检验计算出平均序值差别的临界值域
C D = q α k ( k + 1 ) 6 N (9) CD=q_{\alpha}\sqrt{\frac{k(k+1)}{6N}} \tag9 CD=qα6Nk(k+1)(9)
下表给出了 α \alpha α=0. 05和0. 1时常用的 q α q_{\alpha} qα值。若两个算法的平均序值之差超出了临界值域CD, 则以相应的置信度拒绝“两个算法性能相同”这一假设。
Nemenyi检验中常用的 q α q_{\alpha} qα值:
| α \alpha α\算法个数 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| α = 0.05 \alpha=0.05 α=0.05 | 1.960 | 2.344 | 2.569 | 2.728 | 2.850 | 2.949 | 3.031 | 3.102 | 3.164 |
| α = 0.1 \alpha=0.1 α=0.1 | 1.645 | 2.052 | 2.291 | 2.459 | 2.589 | 2.693 | 2.780 | 2.855 | 2.920 |
以算法比较序值表中的数据为例,先根据式(7)和(8)计算出 τ F = 24.429 \tau_F=24. 429 τF=24.429, 由表2. 6可知,它大于 α = 0.05 \alpha=0. 05 α=0.05时的F检验临界值5. 143, 因此拒绝“所有算法性能相同”这个假设。然后使用 Nemenyi 后续检验,在表2. 7中找到k=3时90. 05=2. 344, 根据式(9)计算出临界值域CD=1. 657,值可知,算法A与B的差距,以及算法B与C的差距均未超过临界值域,而算法A与C的差距超过临界值域,因此检验结果认为算法A与C的性能显者不同,而算法A与B、以及算法B与C的性能没有显著差别。
上述检验比较可以直观地用 Friedman 检验图显示。例如根据算法比较序值表的序值结果可绘制出 Friedman 检验图, 图中纵轴显示各个算法,横轴是平均序值。对每个算法,用一个圆点显示其平均序值,以圆点为中心的横线段表示临界值域的大小。然后就可从图中观察,若两个算法的横线段有交,则说明这两个算法没有显著差别,否则即说明有显著差别。从图2. 8中可容易地看出,算法A与B没有显著差别,因为它们的横线段有交叠区域,而算法A显著优于算法C, 因为它们的横线段没有交叠区域。