《动手学深度学习》——多层感知机
参考资料:
- 《动手学深度学习》
4.1 多层感知机
4.1.1 隐藏层
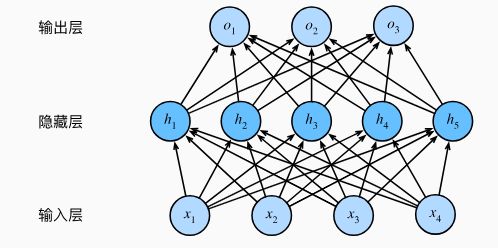
隐藏层 + 激活函数能够模拟任何连续函数。
4.1.2 激活函数
4.1.2.1 ReLu函数
ReLU ( x ) = max ( x , 0 ) \operatorname{ReLU}(x) = \max(x, 0) ReLU(x)=max(x,0)

当输入为负时,ReLU 的导数为 0 ;当输出为负时,ReLU 的导数为 1 。
ReLU的优势在于它的求导非常简单,要么让参数消失,要么让参数通过;并且,ReLU减轻了梯度消失的问题。
4.1.2.2 sigmoid函数
sigmoid ( x ) = 1 1 + exp ( − x ) \operatorname{sigmoid}(x) = \frac{1}{1 + \exp(-x)} sigmoid(x)=1+exp(−x)1
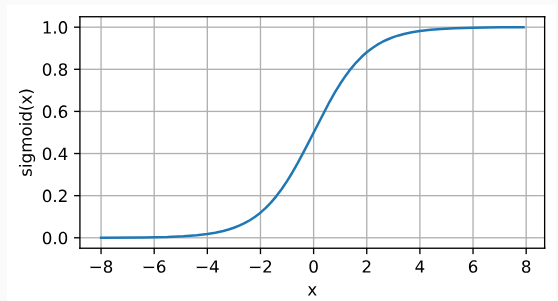
sigmoid 函数的导数为:
d d x sigmoid ( x ) = sigmoid ( x ) ( 1 − sigmoid ( x ) ) \frac{{\rm d}}{{\rm d}x} \operatorname{sigmoid}(x) = \operatorname{sigmoid}(x)\left(1-\operatorname{sigmoid}(x)\right) dxdsigmoid(x)=sigmoid(x)(1−sigmoid(x))

4.1.2.3 tanh函数
tanh ( x ) = 1 − exp ( − 2 x ) 1 + exp ( − 2 x ) \operatorname{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)} tanh(x)=1+exp(−2x)1−exp(−2x)
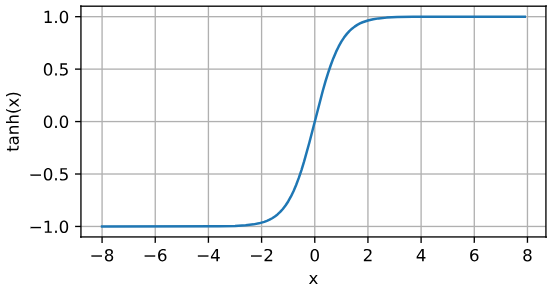
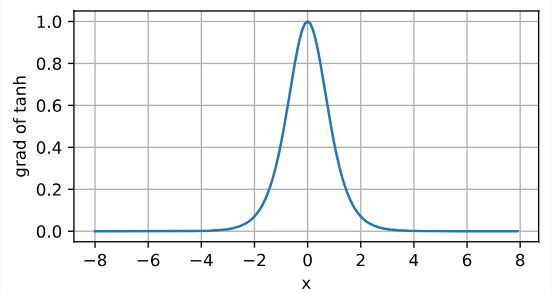
tanh 函数的导数为:
d d x tanh ( x ) = 1 − tanh 2 ( x ) \frac{{\rm d}}{{\rm d}x} \operatorname{tanh}(x) = 1 - \operatorname{tanh}^2(x) dxdtanh(x)=1−tanh2(x)
4.2 多层感知机的从零开始实现
暂略
4.3 多层感知机的简洁实现
4.3.1 模型
假设输入为 28*28 的黑白图片,输出对应 10 个可能的类别,隐含层有 256 个隐藏单元,使用 ReLU 激活函数:
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
4.4 模式选择、欠拟合和过拟合
4.4.1 训练误差和泛化误差
4.4.1.1 统计学习理论
独立同分布假设:训练数据和测试数据都是从相同的分布中独立提取的。
4.4.1.1 模型复杂性
几个倾向于影响模型泛化的因素。
- 可调整参数的数量。当可调整参数的数量(有时称为自由度)很大时,模型往往更容易过拟合。
- 参数采用的值。当权重的取值范围较大时,模型可能更容易过拟合。
- 训练样本的数量。即使模型很简单,也很容易过拟合只包含一两个样本的数据集。而过拟合一个有数百万个样本的数据集则需要一个极其灵活的模型。
4.4.2 模型选择
4.4.2.1 验证集
原则上,在我们确定所有的超参数之前,我们不希望用到测试集。 如果我们在模型选择过程中使用测试数据,可能会有过拟合测试数据的风险。
4.4.2.2 K折交叉验证
原始训练数据被分成 K K K个不重叠的子集。然后执行 K K K次模型训练和验证,每次在 K − 1 K-1 K−1个子集上进行训练,并在剩余的一个子集(在该轮中没有用于训练的子集)上进行验证。最后,通过对 K K K次实验的结果取平均来估计训练和验证误差。
4.4.3 欠拟合还是过拟合?
4.4.3.1 模型复杂度

4.4.3.2 数据集大小
训练数据集中的样本越少,我们就越有可能(且更严重地)过拟合。 随着训练数据量的增加,泛化误差通常会减小。
4.5 权重衰减
4.5.1 范数与权重衰减
我们改写损失函数:
L ( w , b ) + λ 2 ∥ w ∥ 2 L(\mathbf{w}, b) + \frac{\lambda}{2} \|\mathbf{w}\|^2 L(w,b)+2λ∥w∥2
其中, λ \lambda λ 为超参数。引入正则项后,模型更倾向于将让参数逐渐衰减。通常,网络输出层的偏置项不会被正则化。
较小的参数对输入不敏感,所以可能拥有更好的泛化性能。
4.5.2 参数衰减的简洁实现
def train_concise(wd):
...
# 偏置参数没有衰减
trainer = torch.optim.SGD([
{"params":net[0].weight,'weight_decay': wd},
{"params":net[0].bias}], lr=lr)
...
上面的代码中,wd 就是正则项中的 λ \lambda λ .
4.6 暂退法
4.6.1 重新审视过拟合
4.6.2 扰动的稳健性
经典泛化理论认为,为了缩小训练和测试性能之间的差距,应该以简单的模型为目标。
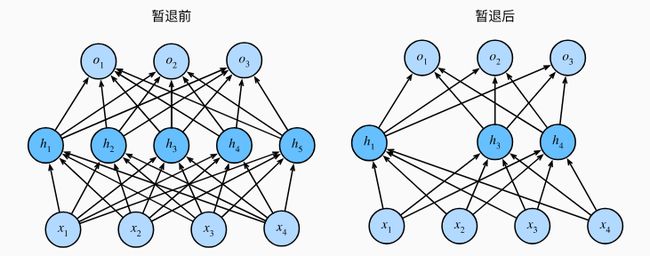
暂退法在前向传播过程中,计算每一内部层的同时注入噪声,在整个训练过程的每一次迭代中,标准暂退法包括在计算下一层之前将当前层中的一些节点置零。通常,我们给中间层活性值 h h h 以暂退概率 p p p 由随机变量 h ′ h' h′ 替换,如下所示:
h ′ = { 0 概率为 p h 1 − p 其他情况 h' = \begin{cases} 0 & \text{ 概率为 } p \\ \frac{h}{1-p} & \text{ 其他情况} \end{cases} h′={01−ph 概率为 p 其他情况
4.6.3 暂退法的简洁实现
dropout1, dropout2 = 0.2, 0.5
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
# 在第一个全连接层之后添加一个dropout层
nn.Dropout(dropout1),
nn.Linear(256, 256),
nn.ReLU(),
# 在第二个全连接层之后添加一个dropout层
nn.Dropout(dropout2),
nn.Linear(256, 10))
4.7 前向传播、反向传播和计算图
暂略。
4.8 数值稳定性和模型初始化
4.8.1 梯度消失和梯度爆炸
由于 Sigmoid 函数的导数在输入距离 0 较远的时候非常接近 0 ,所以在反向传播的时候很可能导致某个参数的梯度为 0 。所以现在人们更倾向于选择 ReLU 函数。
如果深度网络在初始化具有较大的权重矩阵,则多个权重矩阵相乘将导致梯度下降很难收敛。
4.8.2 参数初始化
4.8.2.1 默认初始化
如果我们不指定初始化方法, 框架将使用默认的随机初始化方法,对于中等难度的问题,这种方法通常很有效。
4.8.2.2 Xavier初始化
通常,Xavier初始化从均值为零,方差 σ 2 = 2 n i n + n o u t \sigma^2 = \frac{2}{n_\mathrm{in} + n_\mathrm{out}} σ2=nin+nout2 的高斯分布中采样权重。
4.8.2 参数初始化
4.8.2.1 默认初始化
如果我们不指定初始化方法, 框架将使用默认的随机初始化方法,对于中等难度的问题,这种方法通常很有效。
4.8.2.2 Xavier初始化
通常,Xavier初始化从均值为零,方差 σ 2 = 2 n i n + n o u t \sigma^2 = \frac{2}{n_\mathrm{in} + n_\mathrm{out}} σ2=nin+nout2 的高斯分布中采样权重。