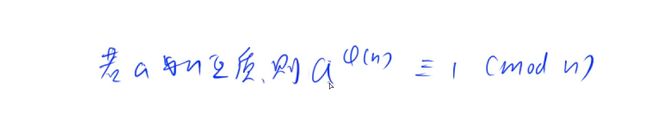第四章 数学知识(二)——欧拉函数,快速幂,扩展欧与中国剩余定理
文章目录
-
- 欧拉函数
-
- 线性筛求欧拉函数
- 欧拉定理
- 快速幂
-
- 逆元
- 扩展欧几里得
- 中国剩余定理
-
- 扩展中国剩余定理
- 欧拉函数练习题
-
- 873. 欧拉函数
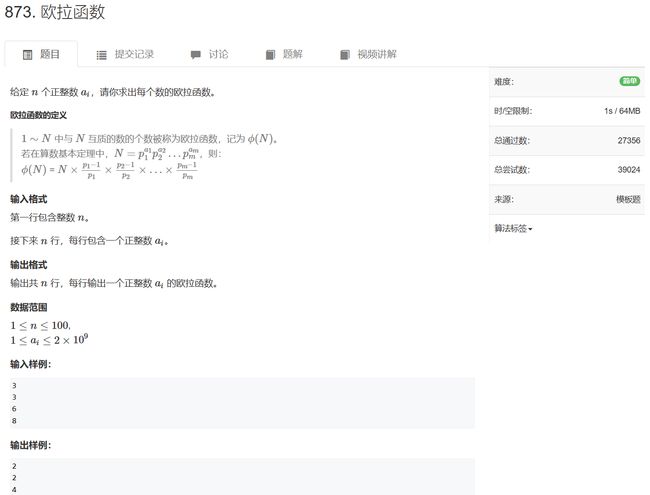
- 874. 筛法求欧拉函数
- 快速幂练习题
-
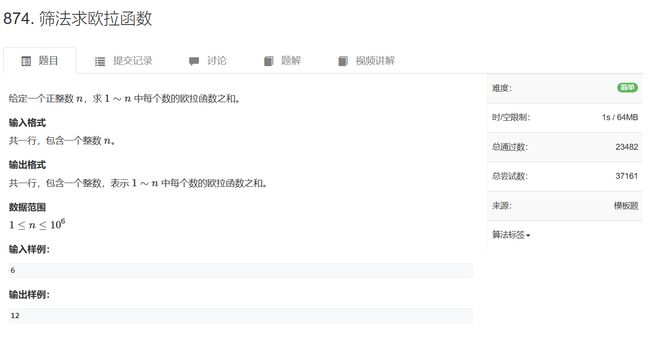
- 875. 快速幂
- 876. 快速幂求逆元
- 扩展欧练习题
-
- 877. 扩展欧几里得算法
- 878. 线性同余方程
- 中国剩余定理练习题
-
- 204. 表达整数的奇怪方式
脑阔疼
欧拉函数
互质:若N个整数的最大公约数是1,那么称这N个数互质
思路是容斥原理:
如何求1~N中和N互质的数的个数?现有质数 p 1 p_1 p1, p 2 p_2 p2, … , p k p_k pk < N
- 从1~N中删除 p 1 p_1 p1, p 2 p_2 p2, … , p k p_k pk 的所有倍数(不包括质数本身)
- 加上两个质数相乘的倍数
- 删除三个质数相乘的倍数
- 加上四个质数相乘的倍数
- …不断重复
为什么会不断重复?因为删除 p 1 p_1 p1, p 2 p_2 p2, … , p k p_k pk 的所有倍数时,可能有的数( p i p_i pi与 p j p_j pj的倍数)被二次删除,导致最终得到的结果变小,所以需要加上被二次删除的数
加上被二次删除的数后,又有些数( p i p_i pi, p j p_j pj与 p k p_k pk的倍数)被二次加上,需要删除这些数
删除被二次加上的时后,又有些数( p i p_i pi, p j p_j pj, p k p_k pk与 p l p_l pl的倍数)被二次删除,需要加上这些数
…不断重复,重复加减k次就能求得欧拉数
N − N p 1 − N p 2 . . . − N p k + N p 1 p 2 + . . . + ( − 1 n − 1 ) N p 1 p 2 . . . p k N-\frac{N}{p_1}-\frac{N}{p_2}...-\frac{N}{p_k}+\frac{N}{p_1p_2}+...+(-1^{n-1})\frac{N}{p_1p_2...p_k} N−p1N−p2N...−pkN+p1p2N+...+(−1n−1)p1p2...pkN
公式类似这样,不断的加减直到分母由k个质数相乘为止
同时公式能够整理成y总板书中的那种格式:
ϕ ( N ) = N ( 1 − 1 p 1 ) ( 1 − 1 p 2 ) ( 1 − 1 p 3 ) . . . ( 1 − 1 p k ) ϕ(N)=N(1-\frac{1}{p_1})(1-\frac{1}{p_2})(1-\frac{1}{p_3})...(1-\frac{1}{p_k}) ϕ(N)=N(1−p11)(1−p21)(1−p31)...(1−pk1)
或者是这种格式:
ϕ ( N ) = N ( p 1 − 1 p 1 ) ( p 2 − 1 p 2 ) ( p 3 − 1 p 3 ) . . . ( p k − 1 p k ) ϕ(N)=N(\frac{p_1-1}{p_1})(\frac{p_2-1}{p_2})(\frac{p_3-1}{p_3})...(\frac{p_k-1}{p_k}) ϕ(N)=N(p1p1−1)(p2p2−1)(p3p3−1)...(pkpk−1)
模板:分解质因数的板子,找到质因数后根据公式进行运算即可
int phi(int n)
{
int res = n;
for (int i = 2; i <= n / i; ++ i )
{
if (n % i == 0)
{
res = res / i * (i - 1);
while (n % i == 0) n /= i;
}
}
if (n > 1) res = res / n * (n - 1);
return res;
}
线性筛求欧拉函数
定义ϕ为欧拉函数,若n是质数,那么ϕ(n) = n - 1,因为2~n-1中没有数能整除n,同时1和n互质,所以1~n-1的所有数都与n互质,即ϕ(n) = n - 1
若要求某个范围内所有数的欧拉数,可以套用线性筛的板子,若当前数是质数,那么ϕ(n) = n - 1
若当前数是合数,在线性筛中分两种情况:用i遍历1~n的所有数,用j遍历当前已经找出的质数
i % primes[j] == 0,说明此时枚举的质数是该合数的最小质因子,而i * primes[j]的最小质因子也是primes[j]。此时的ϕ(i * primes[j])比ϕ(i)多乘了primes[j],所以ϕ(i * primes[j]) = ϕ(i) * primes[j]i % primes[j] != 0,说明此时枚举的质数小于该合数的最小质因子,i * primes[j]的最小质因子为primes[j],此时的ϕ(i * primes[j])比ϕ(i)多乘了primes[j]与(1 - 1/primes[j])。所以此时的ϕ(i * primes[j]) = primes[j] * ϕ(i) * (1 - 1/primes[j]),化简后就是ϕ(i * primes[j]) = ϕ(i) * (primes[j] - 1)
模板:
int eulers[N], primes[N], cnt;
bool st[N];
void get_eulers(int n)
{
eulers[1] = 1;
for (int i = 1; i <= n; ++ i )
{
if (!st[i]) primes[cnt ++ ] = i, eulers[i] = i - 1;
for (int j = 0; primes[j] < n / i; ++ j )
{
int t = i * primes[j];
st[t] = true;
if (i % primes[j] == 0)
{
eulers[t] = primes[j] * eulers[i];
break;
}
eulers[t] = eulers[i] * (eulers[i] - 1);
}
}
}
欧拉定理
先说明一个简单的性质:如果ac≡bc(mod m),并且c和m互质,则a≡b(mod m)
证明:
首先,当a = b或者c = 1时,a≡b(mod m)成立
当a > b并且c ≠ 1时,ac ≡bc(mod m)等价于ac = bc + km
整理得:c(a - b) = km,a - b = km / c
因为a - b是正整数,并且c和m互质,即m / c一定不为整数
所以k / c一定为整数,即a = b + k’m,等价于a ≡ b (mod m)
证明完毕,举个反例,当a = 2, b = 4, c = 2, m = 4时,c和m不互质
此时2 * 2 ≡ 2 * 4 (mod 4),两边同除2
2 ≡ 4 (mod 4)显然不成立
总之:记住这个结论,很常用。c和m互质的情况下,不论是两边同乘c还是同除c都是成立的
证明欧拉定理:
a a a与 n n n互斥,1~n中,与 n n n互质的数有 a 1 a_1 a1, a 2 a_2 a2, … , a ϕ ( n ) a_{ϕ(n)} aϕ(n)
a a a与 n n n互斥并且 a i a_i ai与 n n n互质
所以 a a a * a 1 a_1 a1, a a a * a 2 a_2 a2, … , a a a * a ϕ ( n ) a_{ϕ(n)} aϕ(n)也是与n互质的
现证明 a a a * a i a_i ai与 a a a * a j a_j aj不相同,即 a a a * a 1 a_1 a1, a a a * a 2 a_2 a2, … , a a a * a ϕ ( n ) a_{ϕ(n)} aϕ(n)两两不同
用反证法:假设 a a a * a i a_i ai与 a a a * a j a_j aj相同,那么有 a a a * a i a_i ai ≡ a a a * a j a_j aj (mod n)
因为 a a a与 n n n互质,所以 a i a_i ai ≡ a j a_j aj (mod n),与前提 a 1 a_1 a1, a 2 a_2 a2, … , a ϕ ( n ) a_{ϕ(n)} aϕ(n)是1~n中与n互质的数矛盾
所以 a a a * a 1 a_1 a1, a a a * a 2 a_2 a2, … , a a a * a ϕ ( n ) a_{ϕ(n)} aϕ(n)中,不存在相同的两个数
即 a a a * a 1 a_1 a1, a a a * a 2 a_2 a2, … , a a a * a ϕ ( n ) a_{ϕ(n)} aϕ(n)是互不相同且与n互质的数
因为 a 1 a_1 a1, a 2 a_2 a2, … , a ϕ ( n ) a_{ϕ(n)} aϕ(n)也是互不相同且与n互质的数
所以 a 1 a_1 a1 * a 2 a_2 a2 * … * a ϕ ( n ) a_{ϕ(n)} aϕ(n) ≡ a a a * a 1 a_1 a1, a a a * a 2 a_2 a2, … , a a a * a ϕ ( n ) a_{ϕ(n)} aϕ(n) (mod n)
整理得 a 1 a_1 a1 * a 2 a_2 a2 * … * a ϕ ( n ) a_{ϕ(n)} aϕ(n) ≡ a ϕ ( n ) a^ {ϕ(n)} aϕ(n) * a 1 a_1 a1, * a 2 a_2 a2 * … * a ϕ ( n ) a_{ϕ(n)} aϕ(n) (mod n)
由于 a i a_i ai与n互质,所以两边同除 a 1 a_1 a1 * a 2 a_2 a2 * … * a ϕ ( n ) a_{ϕ(n)} aϕ(n)
得到 a ϕ ( n ) a^ {ϕ(n)} aϕ(n) ≡ 1 (mod n)
证明完毕
注意欧拉定理的前提是a与n互质
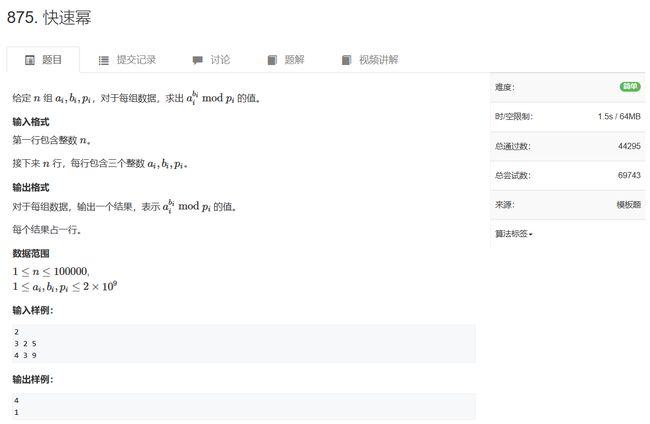
特别的当n为质数时,有结论: a n − 1 a^ {n-1} an−1 ≡ 1 (mod n)
这是费马小定理
快速幂
在O(logk) 的时间复杂度下,快速地求出 a k a^k ak % p的结果
计算n每个因子%p的结果,然后将这些结果相乘再%p,得到的结果和n % p相同
预处理:将 a k a^k ak分解成 a 2 i a^{2^i} a2i,也就是将k拆分成多个 2 i 2^i 2i,其中i范围为:0~logk
当i等于logk时, 2 i 2^i 2i = k。我们需要选择一些 2 i 2^i 2i,使它们相加等于k
也就是k的二进制表示中,1在哪一位上,i就是几
比如k = 5,5的二进制表示101,那么5就可以拆分成: 2 0 2^0 20 + 2 2 2^2 22
k k k作为 a a a的指数,那么 a a a的 k k k次方就可以根据k的拆分,被拆分成多个式子相乘(最多32或64个式子)
比如 a 5 a^5 a5 被拆分成 a 2 0 a^{2^0} a20 * a 2 2 a^{2^2} a22,要求 a k a^k ak % p p p,可以将 a k a^k ak进行拆分,将拆分后每个式子% p p p的结果相乘,最后再% p p p即可
如何用代码实现?
k的二进制表示中,有几个1, a k a^k ak就能被拆分成几个式子相乘
当k的第i位为1,表示式子 a 2 i a^{2^i} a2i需要累乘
我们不断右移k,同时让a不断自乘( a 1 a^1 a1, a 2 a^2 a2, a 4 a^4 a4, a 8 a^8 a8…)。当k的第i位为1,直接* a % p
模板:
int qmi(int a, int k, int p)
{
lont lont res = 1;
while (k)
{
if (k & 1) res = res * a % p;
a = (long long)a * a % p;
k >>= 1;
}
return res;
}
逆元
在数论问题中,我们不希望进行除法运算,因为除法可能得到小数,处理小数很麻烦
我们希望进行乘法运算,乘法运算只会得到整数,处理整数是很方便的
所以当一个数作为除数参数运算时,我们希望它能作为一个乘数参与运算
对于一个除数b,若存在一个整数x,使得用x做乘法运算的结果,与原除法运算结果相同,那么x就是b的乘法逆元。可以用以下式子表示:
a / b ≡ a * x (mod m)
注意:这里运算的结果需要取模m,结果相同也意味着运算并取模m后的结果相同,乘法逆元更准确的叫法是模m乘法逆元
b b b的模m乘法逆元用 b − 1 b^{-1} b−1表示,需要与 b b b的逆做区分
整理式子: a / b ≡ a ∗ x ( m o d m ) a / b ≡ a * x (mod\ m) a/b≡a∗x(mod m)
两边同乘 b b b得到
a ≡ b ∗ a ∗ b − 1 ( m o d m ) a ≡ b * a * b^{-1} (mod\ m) a≡b∗a∗b−1(mod m)
式子两边同除 a a a得到:
b ∗ b − 1 ≡ 1 ( m o d m ) b * b^{-1} ≡ 1(mod\ m) b∗b−1≡1(mod m)
当m是质数时,根据费马定理:
b m − 1 ≡ 1 ( m o d m ) b^{m - 1} ≡ 1 (mod\ m) bm−1≡1(mod m)
整理得:
b ∗ b m − 2 ≡ 1 ( m o d m ) b * b^{m - 2} ≡ 1 (mod\ m) b∗bm−2≡1(mod m)
经过对比,在m质数的情况下,我们要求的 b − 1 b^{-1} b−1等价于 b m − 2 b^{m -2} bm−2
综上, b b b的模m乘法逆元为 b m − 2 b^{m -2} bm−2,已知 b b b和 m m m即可直接求出逆元
所以求逆元的本质就是快速幂,板子和快速幂一样,参数为qmi(b, m - 2, m)
扩展欧几里得
裴蜀定理:对于任意整数(a, b)一定存在非零整数(x, y)使得
ax + by = d,其中d是(a, b)的最大公约数
裴蜀定理证明:(a, b)的最大公约数d能够整除a与b,可知d | ax + by。假设ax + by = D,那么D就能被d整除,将式子乘以d/D,就能得到a'x + b'y = d
即存在非零整数a’与b’使得a'x + b'y = d,证明完毕
扩展欧几里得:求解系数
(x, y)使得式子ax + by = d成立,其中d是(a, b)的最大公约数
用(a, b)表示a与b的最大公约数,在欧几里得算法中,我们证明过(a, b) = (b, a % b)
若等式ax + by = d (1)成立,那么等式(a % b)x' + by' = d也会成立,整理等式使两式格式相同:
( a − [ a / b ] b ) x ′ + b y ′ = d (a - [a/b]b) x' + by' = d (a−[a/b]b)x′+by′=d
整理a与b的系数:
a x ′ + b ( y ′ − [ a / b ] x ′ ) = d ( 2 ) ax'+b(y'-[a/b]x')=d\ (2) ax′+b(y′−[a/b]x′)=d (2)
对比(1)式与(2)式,要使两式相同,那么(2)式中a的系数x' = x,b的系数y' - [a/b]x' = y
也就是说,若我们知道系数(x', y')使式子(a % b)x' + by' = d成立,那么我们就能求得系数(x, y)使得式子ax + by = d成立
在欧几里得算法中,我们通过递归使得(a, b)中的b不断地接近0,当b为0时,向下递归结束,程序将向上递归
若b = 0,此时使式子ax + by = d成立的(x, y)的值为(1, 0)
带入递归过程,每一次向下递归都是将(a. b)转换成(b, a % b)
在裴蜀定理中,a和b的转换导致了其系数(x, y)向(x', y')的转换,现已知最终的系数(1, 0)
它是一次递归过程中的(x', y'),我们可以推导出该递归过程中的(x, y)
然后将其作为上一个递归过程的(x', y'),不断地向上递归,直到推导出首个递归过程的(x, y),此时求解完成
模板:
// 函数返回最大公约数,扩展欧的系数(x, y)通过输出型参数返回
int exgcd(int a, int b, int& x, int& y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
中国剩余定理
给定一组互质的数 m i m_i mi,和数量相同的另一组数 a i a_i ai,可以构造出x,使x与 m i m_i mi互质并且满足以下线性方程组

x在模 m i m_i mi的情况下是唯一的
首先M表示所有 m i m_i mi的乘积, M i M_i Mi表示M / m i m_i mi
那么有通解:
x = a 1 M 1 M 1 − 1 + a 2 M 2 M 2 − 1 + . . . + a k M k M k − 1 x = a_1M_1M_1^{-1}+a_2M_2M_2^{-1}+...+a_kM_kM_k^{-1} x=a1M1M1−1+a2M2M2−1+...+akMkMk−1
来看为什么这个通解成立,在mod m 1 m_1 m1的情况下,只有 M 1 M_1 M1 M 1 − 1 M_1^{-1} M1−1 = 1, M i M_i Mi M i − 1 M_i^{-1} Mi−1 = 0
因为 M i M_i Mi中含有因子 m 1 m_1 m1,所以 m 1 m_1 m1能够整除 M i M_i Mi
扩展中国剩余定理
中国剩余定理用于解决一组互质模同余方程问题
而扩展中国剩余定理用于解决一组不互质模同余方程问题,即 m i m_i mi之间不互质
同余方程的形式是:
x ≡ a i ( m o d m i ) x ≡ a_i (mod\ m_i) x≡ai(mod mi)
变形一下有:
x = a i + k m i x = a_i+ k m_i x=ai+kmi
同时x要满足另一同余方程:x = a j a_j aj + k * m j m_j mj,联立两式可以得到:
a i + k i m i = a j + k j m j a_i + k_im_i = a_j + k_jm_j ai+kimi=aj+kjmj
整理得:
k i m i − k j m j = a j − a i k_im_i - k_jm_j= a_j - a_i kimi−kjmj=aj−ai
这个式子可以用扩展欧求解,假设(a, b)的最大公约数为d
( m i m_i mi, m j m_j mj)对应(a, b),( k i k_i ki, k j k_j kj)对应(a, b)的系数(x, y),若( a j a_j aj - a i a_i ai )是d的倍数,那么( k i k_i ki, k j k_j kj)有解
否则无解
求出一对特解后,令
k i = k i + m j d k , k j = k j + m i d k ( k = . . . , − 2 , − 1 , 0 , 1 , 2 , . . . ) k_i = k_i+\frac{m_j}{d}k,\ k_j = k_j+\frac{m_i}{d}k\ (k = ...,-2,-1,0, 1, 2,...) ki=ki+dmjk, kj=kj+dmik (k=...,−2,−1,0,1,2,...)
通过特解就能求出通解(将通解带入等式 a i a_i ai + k i k_i ki * m i m_i mi = a j a_j aj + k j k_j kj * m j m_j mj,等式依然成立)
为什么 m i m_i mi与 m j m_j mj要除以d?为了保证此时计算出的特解互质,以提高求出完整特解的速度
回到一开始的式子:x = a i a_i ai + k i k_i ki * m i m_i mi,计算出通解后将通解带入式子
x = a i + ( k i + m j d k ) m i x=a_i + (k_i+\frac{m_j}{d}k)m_i x=ai+(ki+dmjk)mi
展开得到:
x = a i + k i m i + m i m j d k x=a_i + k_im_i+\frac{m_im_j}{d}k x=ai+kimi+dmimjk
再证明一个常用的性质:gcd(a, b) * lcm(a, b) = a * b
a与b的最大公约数与最小公倍数的乘积等于a与b的乘积
使用分解质因数法证明:
假设最大公约数为d,最小公倍数为m
将a和b质因数分解:a = d * p1* p2 * ... * pr, b = d * q1 * q2 * ... * qs
其中d是a和b中相同的质因数,也就是最小公约数
那么m就是所有质因数的乘积m = d * p1* p2 * ... * pr * q1 * q2 * ... * qs
那么ab = dm
证明完毕
所以 m i m_i mi m j m_j mj/d = m,m为 m i m_i mi和 m j m_j mj最小公倍数,等式为:
x = a i + k i m i + k m ( k = . . . , − 2 , − 1 , 0 , 1 , 2... ) x=a_i + k_im_i+km\ (k = ...,-2,-1,0, 1, 2...) x=ai+kimi+km (k=...,−2,−1,0,1,2...)
其中 a i a_i ai和 k i k_i ki m i m_i mi是已知的数,可以将整个式子看成
x = c + k m x = c + km x=c+km
也就是x ≡ c (mod m)
最终要求的是最小非负整数x,转换这个式子:
x = k 1 m + c ′ x = k_1m + c' x=k1m+c′
对于c,有:
c = k 2 m + c ′ c=k_2m+c' c=k2m+c′
两式的c’在m的剩余系中,并且c’相同,只有 k 1 k_1 k1和 k 2 k_2 k2不同,根据c’合并两式
c = k 2 m + ( x − k 1 m ) c=k_2m+(x-k_1m) c=k2m+(x−k1m)
整理得:
c = ( k 2 − k 1 ) m + x c=(k_2-k_1)m+x c=(k2−k1)m+x
可以看成c ≡ x (mod m),要求最小非负整数,x就要在m的剩余系中,所以x = c mod m
而c = k i k_i ki m i m_i mi + a i a_i ai, a i a_i ai和 m i m_i mi已知, k i k_i ki根据扩展欧求得,所以c是已知的,m是( m i m_i mi, m j m_j mj)的最小公倍数,根据扩展欧也能求得。所以x = c mod m中,只有x未知,其他参数已知,那么x就能被求出,最终求x的式子是:
x = c m o d m x = c\ mod\ m x=c mod m
但是这个x只是满足两个线性同余方程的通解,要让x满足所有线性同余方程,就要重复上面的步骤(n - 1)次(假设方程有n个)。重复操作如何进行?对某两个线性同余方程求出通解后,有式子:
x = a i + k i m i + k m ( k = . . . , − 2 , − 1 , 0 , 1 , 2... ) x=a_i + k_im_i+km\ (k = ...,-2,-1,0, 1, 2...) x=ai+kimi+km (k=...,−2,−1,0,1,2...)
而第i个线性同余方程是:
x = k i m i + a i x=k_im_i+a_i x=kimi+ai
将通解中的 a i a_i ai+ k i k_i ki m i m_i mi作为新的 a i a_i ai, m m m作为新的 m i m_i mi,得到一个新的线性同余方程,将其与第k个线性同余方程联立,重复以上所有操作,求出满足两式的非负最小x
用于每次联立两式求出的x满足非负最小,重复n - 1求出的x也满足非负最小,局部最优推出全局最优,所以一定能保证对于所有的方程来说,x是非负最小的
总结下:通过扩展欧求特解,通过特解求通解,通过通解求x,重复n - 1次
模板:
typedef long long LL;
LL exgcd(LL a, LL b, LL &x, LL &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
LL d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
LL ai, aj, mi, mj, ki, kj;
LL x = 0;
int n;
scanf("%d", &n);
scanf("%ld%ld", &mi, &ai);
for (int i = 0; i < n - 1; ++ i )
{
scanf("%ld%ld", &mj, &aj);
LL d = exgcd(mi, mj, ki, kj);
if ((aj - ai) % d)
{
x = -1;
break;
}
ki = (aj - ai) / d * ki;
LL t = mj / d;
ki = (ki % t + t) % t;
// 用通解更新ai和mi,使两式合并
ai = ai + ki * mi;
mi = mi / d * mj;
}
if (x != -1) x = (ai % mi + mi) % mi;
printf("%ld\n", x);
欧拉函数练习题
873. 欧拉函数
#include 874. 筛法求欧拉函数
#include 快速幂练习题
875. 快速幂
#include 876. 快速幂求逆元
需要注意的是:题目保证p是一个质数,所以当a为p的倍数时,无法使用费马定理,逆元也就不存在
#include 扩展欧练习题
877. 扩展欧几里得算法
#include 878. 线性同余方程
等式ax ≡ b (mod m),当b <= m时,等式可以变形成ax = b + my,令y' = y,整理得ax + my' = b,题目给定a, m b,要求a的系数x
利用扩展欧可以求解两个系数x, y',不过使用扩展欧的前提是ax + my' = b,其中的b需要是(a, m)的最大公约数的倍数
也就是扩展欧需要先满足裴蜀定理,当b % (a, m) != 0时,扩展欧无法使用,等式无解
#include debug:在b % d != 0的情况下,ax + my = b与ax' + my' = d也是倍数关系,题目要返回的是x,而我们只求得x’,所以需要进行转换,输出b / d * x
不能输出x / d * b,因为x与d可能不是倍数关系,这样计算的结果将出现偏差
或者输出x * b / d也行,不过要注意long long的强转,防止爆int
最后需要保证答案在mod m剩余系中,所以要mod m
中国剩余定理练习题
204. 表达整数的奇怪方式
#include