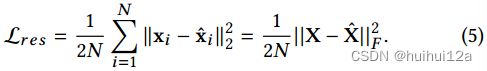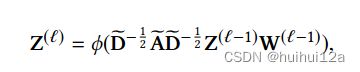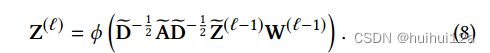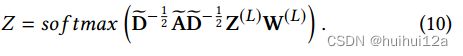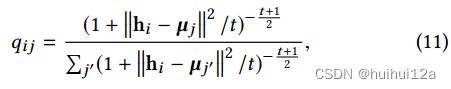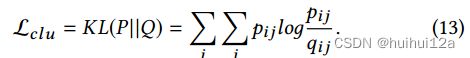Structural Deep Clustering Network
Structural Deep Clustering Network | Proceedings of The Web Conference 2020 (acm.org)
目录
Abstract
1 Introduction
2 Model
2.1 KNN Graph
2.2 DNN Module
2.3 GCN Module
2.4 Dual Self-Supervised Module
3 代码注释
Abstract
深度聚类方法通常是通过深度学习强大的表示能力来提升聚类结果,例如自动编码器,这表明学习一个有效的聚类表示是一个至关重要的要求。
深度聚类方法的优势在于从数据本身中提取有用表示,但很少从数据结构中提取有用表示。因为GCN在提取图结构编码方面取得了很大成功。作者提出了一种结构深度聚类网络(SDCN),将结构信息整合到深度聚类中。即设计了一个传递算子将自编码器学习到的表征传递到相应的GCN层,并设计了一个双重自监督机制来统一这两种不同的深度神经结构并指导整个模型的更新。通过这种方式,从低阶到高阶的多种数据结构,自然地与自编码器学习到的多种表示相结合。此外,作者从理论上分析了传递算子,通过传递算子,GCN将特定于自编码器的表示改进为高阶图正则化约束,而自编码器有助于缓解GCN中的过度平滑问题。
1 Introduction
深度聚类取得了成功,可以为聚类任务学习不错的表示。但它们通常关注数据本身的特征,因此在学习表示时很少考虑数据的结构,这种结构揭示了样本之间潜在的相似性。
将结构信息整合到深度聚类中通常要解决以下两个问题:(1)深度聚类应该考虑哪些结构信息结构信息?表明了数据样本之间潜在的相似性。然而,数据的结构通常是非常复杂的,即不仅存在样本之间的直接关系(也称为一阶结构),而且存在高阶结构。高阶结构从样本之间的多跳关系施加相似性约束。以二阶结构为例,这意味着对于没有直接关系的两个样本,如果它们有许多共同的邻居样本,它们应该仍然具有相似的表示。当数据结构是稀疏的时候,高阶结构就显得尤为重要。因此,仅利用低阶结构进行深度聚类是远远不够的,如何有效地考虑高阶结构是首先要解决的问题;(2)结构信息与深度聚类之间的关系是什么?深度聚类例如自编码器,网络结构非常复杂,由多层组成。每一层捕获不同的潜在信息。数据之间还存在各种类型的结构信息。那么,在自动编码器中,不同的结构和不同的层之间是什么关系呢?人们可以使用结构以某种方式正则化自编码器学习的表示,然而,另一方面,人们也可以直接从结构本身学习表示。如何将数据结构与自编码器结构结合是另一个问题。
(1)捕获结构信息。构建KNN图,该图能够揭示数据的底层结构。为了从KNN图中捕获低阶和高阶结构信息,提出了一个由多个图卷积层组成的GCN模块,以学习特定于GCN的表示。
(2)将结构信息引入到深度聚类中。引入了一个自编码器模块来从原始数据中学习自编码器特定的表示,并提出了一个传递算子将其与gcn特定的表示结合起来。从理论上证明了传递算子能够更好地辅助自编码器与GCN的集成。特别地,证明了GCN为自编码器学习的表示提供了近似的二阶图正则化,并且自编码器学习的表示可以缓解GCN中的过平滑问题。
(3)由于自编码器和GCN模块都将输出表示,提出了一个双自监督模块来统一引导这两个模块。通过双自监督模块,可以对整个模型进行端到端聚类训练。
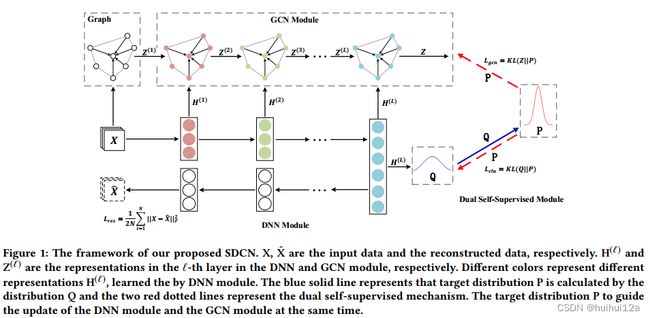
2 Model
模型的整体结构:首先基于原始数据构造一个KNN图。然后将原始数据和KNN图分别输入到自编码器和GCN中;将自编码器的每一层与相应的GCN层连接起来,这样就可以通过传递算子将特定于自编码器的表示集成到结构感知的表示中;提出了一种双重自监督机制来监督自编码器和GCN的训练进度
2.1 KNN Graph
假设有原始数据X是(N,d),N是样本个数,d是维度,每一行xi代表第i个样本。计算相似性矩阵,然后对于每一个样本,首先找到它top-K相似的邻居,并在它和邻居之间设置边来连接,构建无向k近邻图,这样就可以从非图数据中得到邻接矩阵A。相似性矩阵的计算方法有:
1)Heat Kernel
适合于连续数据
2) Dot-product
适合于离散数据
2.2 DNN Module
为了通用性,使用基本的自编码器学习原始数据表示,来适应不同类型的数据特征。
编码器部分,![]() 是原始数据X
是原始数据X
编码器部分之后是解码器部分,解码器部分是通过该方程通过几个完全连接的层重构输入数据。
解码器的输出是原始数据的重构![]() ,目标函数如下:
,目标函数如下:
2.3 GCN Module
自编码器能够从数据本身学习有用的表示,例如H (1), H(2),···,H (L),而忽略样本之间的关系。本节介绍如何使用GCN模块来传播由DNN模块生成的这些表示。一旦将DNN模块学习到的所有表示集成到GCN中,那么GCN可学习的表示将能够容纳两种不同的信息,即数据本身和数据之间的关系
GCN的传播公式如下:
考虑到自编码器学习到的表示![]() 能够重构数据本身,并且包含不同的有价值信息,将
能够重构数据本身,并且包含不同的有价值信息,将![]() 和
和![]() 两个表示组合在一起,得到一个更完整、更强大的表示:
两个表示组合在一起,得到一个更完整、更强大的表示:
之后将![]() 作为GCN中第l层的输入来生成表示
作为GCN中第l层的输入来生成表示![]() :
:
式(8)可以看出特定于自编码器的表示![]() 将通过归一化邻接矩阵进行传播。由于每个DNN层学习到的表示是不同的,为了尽可能地保留信息,将每个DNN层学习到的表示转移到相应的GCN层进行信息传播。
将通过归一化邻接矩阵进行传播。由于每个DNN层学习到的表示是不同的,为了尽可能地保留信息,将每个DNN层学习到的表示转移到相应的GCN层进行信息传播。
GCN的第一层的输入式原始的数据X。GCN模块的最后一层是具有softmax功能的多分类层:
结果zij∈Z表示概率样本i属于聚类中心j,可以将Z视为一个概率分布。
2.4 Dual Self-Supervised Module
目前经在神经网络架构中将自编码器与GCN连接起来。然而,但它们不是为深度聚类而设计的。基本上,自编码器主要用于数据表示学习,属于无监督学习场景,而传统GCN属于半监督学习场景。这两种方法都不能直接用于聚类。
本文提出了一种双自监督模块,将自编码器和GCN模块统一在一个统一的框架中,并有效地对两个模块进行端到端聚类训练。
对于第i个样本和第j个聚类,使用Student 's t-分布作为核来度量数据表示hi与聚类中心向量µj之间的相似性:
其中![]() 是
是![]() 的第i行,
的第i行,![]() 是通过预训练自编码器学习到的表示经过K-means初始化的。
是通过预训练自编码器学习到的表示经过K-means初始化的。![]() 可以认为是将样本i分配给聚类j的概率,是一种软分配。将Q = [qij]作为所有样本分配的分布。
可以认为是将样本i分配给聚类j的概率,是一种软分配。将Q = [qij]作为所有样本分配的分布。
在获得聚类结果分布Q后,目标是通过学习高置信度分布来优化数据表示。具体来说,希望使数据表示更接近集群中心,从而提高集群的内聚性。计算目标分布如下:
在目标分布P中,对Q中的每个赋值进行平方和归一化处理,使赋值具有更高的置信度。目标函数如下:
最小化Q和P分布之间的KL散度损失,目标分布P可以帮助DNN模块学习更好的聚类任务表示,即使数据表示更靠近聚类中心。这被认为是一种自监督机制,因为目标分布P是由分布Q计算的,而P分布反过来监督分布Q的更新。
对于GCN模块的训练,一种可能的方法是将聚类分配作为真值标签。然而,这种策略会带来噪音和琐碎的解决方案,并导致整个模型的崩溃。2.3节提到,GCN也会提供一个聚类分布Z,因此,可以用分布P来监督分布Z:
目标函数有两个优点:(1)与传统的多分类损失函数相比,KL散度以更“温和”的方式更新整个模型,防止数据表示受到严重干扰;(2) GCN和DNN模块都统一在同一个优化目标上,使得它们的结果在训练过程中趋于一致。由于DNN模块和GCN模块的目标是近似目标分布P,这两个模块之间有很强的联系,称之为双重自监督机制。
SDCN可以直接将两个不同的目标,即聚类目标和分类目标集中在一个损失函数中。因此,提出的SDCN的整体损失函数为:
经过训练直到最大epoch, SDCN将得到一个稳定的结果。然后可以将标签设置为样品。选择分布Z中的软赋值作为最终聚类结果。
因为GCN学习到的表示包含两种不同的信息。分配给样品i的标签为:
3 代码注释
sdcn.py
from __future__ import print_function, division
import argparse
import random
import numpy as np
from sklearn.cluster import KMeans
from sklearn.metrics.cluster import normalized_mutual_info_score as nmi_score
from sklearn.metrics import adjusted_rand_score as ari_score
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.parameter import Parameter
from torch.optim import Adam
from torch.utils.data import DataLoader
from torch.nn import Linear
from utils import load_data, load_graph
from GNN import GNNLayer
from evaluation import eva
from collections import Counter
# torch.cuda.set_device(1)
class AE(nn.Module):
def __init__(self, n_enc_1, n_enc_2, n_enc_3, n_dec_1, n_dec_2, n_dec_3,
n_input, n_z):
super(AE, self).__init__()
self.enc_1 = Linear(n_input, n_enc_1)
self.enc_2 = Linear(n_enc_1, n_enc_2)
self.enc_3 = Linear(n_enc_2, n_enc_3)
self.z_layer = Linear(n_enc_3, n_z)
self.dec_1 = Linear(n_z, n_dec_1)
self.dec_2 = Linear(n_dec_1, n_dec_2)
self.dec_3 = Linear(n_dec_2, n_dec_3)
self.x_bar_layer = Linear(n_dec_3, n_input)
def forward(self, x):
enc_h1 = F.relu(self.enc_1(x))
enc_h2 = F.relu(self.enc_2(enc_h1))
enc_h3 = F.relu(self.enc_3(enc_h2))
z = self.z_layer(enc_h3)
dec_h1 = F.relu(self.dec_1(z))
dec_h2 = F.relu(self.dec_2(dec_h1))
dec_h3 = F.relu(self.dec_3(dec_h2))
x_bar = self.x_bar_layer(dec_h3)
return x_bar, enc_h1, enc_h2, enc_h3, z
class SDCN(nn.Module):
def __init__(self, n_enc_1, n_enc_2, n_enc_3, n_dec_1, n_dec_2, n_dec_3,
n_input, n_z, n_clusters, v=1):
super(SDCN, self).__init__()
# autoencoder for intra information
self.ae = AE(
n_enc_1=n_enc_1,
n_enc_2=n_enc_2,
n_enc_3=n_enc_3,
n_dec_1=n_dec_1,
n_dec_2=n_dec_2,
n_dec_3=n_dec_3,
n_input=n_input,
n_z=n_z)
# 加载预训练的自编码器
self.ae.load_state_dict(torch.load(args.pretrain_path, map_location='cpu'))
# GCN for inter information
self.gnn_1 = GNNLayer(n_input, n_enc_1)
self.gnn_2 = GNNLayer(n_enc_1, n_enc_2)
self.gnn_3 = GNNLayer(n_enc_2, n_enc_3)
self.gnn_4 = GNNLayer(n_enc_3, n_z)
self.gnn_5 = GNNLayer(n_z, n_clusters)
# cluster layer
self.cluster_layer = Parameter(torch.Tensor(n_clusters, n_z))
torch.nn.init.xavier_normal_(self.cluster_layer.data)
# degree
self.v = v
def forward(self, x, adj):
# DNN Module
x_bar, tra1, tra2, tra3, z = self.ae(x)
sigma = 0.5
# GCN Module
# 结和z(l-1)与H(l-1)产生z(l)
h = self.gnn_1(x, adj)
h = self.gnn_2((1-sigma)*h + sigma*tra1, adj)
h = self.gnn_3((1-sigma)*h + sigma*tra2, adj)
h = self.gnn_4((1-sigma)*h + sigma*tra3, adj)
h = self.gnn_5((1-sigma)*h + sigma*z, adj, active=False)
# Z的分布
predict = F.softmax(h, dim=1)
# Dual Self-supervised Module
# Q的分布
q = 1.0 / (1.0 + torch.sum(torch.pow(z.unsqueeze(1) - self.cluster_layer, 2), 2) / self.v)
q = q.pow((self.v + 1.0) / 2.0)
q = (q.t() / torch.sum(q, 1)).t()
return x_bar, q, predict, z
def target_distribution(q):
# P的分布
weight = q**2 / q.sum(0)
return (weight.t() / weight.sum(1)).t()
def train_sdcn(dataset):
model = SDCN(500, 500, 2000, 2000, 500, 500,
n_input=args.n_input,
n_z=args.n_z,
n_clusters=args.n_clusters,
v=1.0).to(device)
print(model)
optimizer = Adam(model.parameters(), lr=args.lr)
# KNN Graph
adj = load_graph(args.name, args.k)
adj = adj.cuda()
# cluster parameter initiate
data = torch.Tensor(dataset.x).to(device)
y = dataset.y
with torch.no_grad():
_, _, _, _, z = model.ae(data)
kmeans = KMeans(n_clusters=args.n_clusters, n_init=20)
y_pred = kmeans.fit_predict(z.data.cpu().numpy())
y_pred_last = y_pred
# 根据自编码器学习的嵌入,和Kmeans算法产生聚类中心
model.cluster_layer.data = torch.tensor(kmeans.cluster_centers_).to(device)
eva(y, y_pred, 'pae')
for epoch in range(200):
if epoch % 1 == 0:
# update_interval
_, tmp_q, pred, _ = model(data, adj)
# Q的分布
tmp_q = tmp_q.data
# 目标P的分布
p = target_distribution(tmp_q)
# 根据三个分布分别计算出样本的聚类结果
res1 = tmp_q.cpu().numpy().argmax(1) #Q
res2 = pred.data.cpu().numpy().argmax(1) #Z
res3 = p.data.cpu().numpy().argmax(1) #P
# 计算三个分类结果和真实分类结果的误差
eva(y, res1, str(epoch) + 'Q')
eva(y, res2, str(epoch) + 'Z')
eva(y, res3, str(epoch) + 'P')
x_bar, q, pred, _ = model(data, adj)
# 计算分布Q和分布P之间的KL散度
kl_loss = F.kl_div(q.log(), p, reduction='batchmean')
# 计算GCN产生的分布Z和P之间的KL散度
ce_loss = F.kl_div(pred.log(), p, reduction='batchmean')
# 自编码器的重构损失
re_loss = F.mse_loss(x_bar, data)
# 综合三种损失
loss = 0.1 * kl_loss + 0.01 * ce_loss + re_loss
optimizer.zero_grad()
loss.backward()
optimizer.step()
if __name__ == "__main__":
parser = argparse.ArgumentParser(
description='train',
formatter_class=argparse.ArgumentDefaultsHelpFormatter)
parser.add_argument('--name', type=str, default='reut')
parser.add_argument('--k', type=int, default=3)
parser.add_argument('--lr', type=float, default=1e-3)
parser.add_argument('--n_clusters', default=3, type=int)
parser.add_argument('--n_z', default=10, type=int)
parser.add_argument('--pretrain_path', type=str, default='pkl')
args = parser.parse_args()
args.cuda = torch.cuda.is_available()
print("use cuda: {}".format(args.cuda))
device = torch.device("cuda" if args.cuda else "cpu")
args.pretrain_path = 'data/{}.pkl'.format(args.name)
dataset = load_data(args.name)
if args.name == 'usps':
args.n_clusters = 10
args.n_input = 256
if args.name == 'hhar':
args.k = 5
args.n_clusters = 6
args.n_input = 561
if args.name == 'reut':
args.lr = 1e-4
args.n_clusters = 4
args.n_input = 2000
if args.name == 'acm':
args.k = None
args.n_clusters = 3
args.n_input = 1870
if args.name == 'dblp':
args.k = None
args.n_clusters = 4
args.n_input = 334
if args.name == 'cite':
args.lr = 1e-4
args.k = None
args.n_clusters = 6
args.n_input = 3703
print(args)
train_sdcn(dataset)