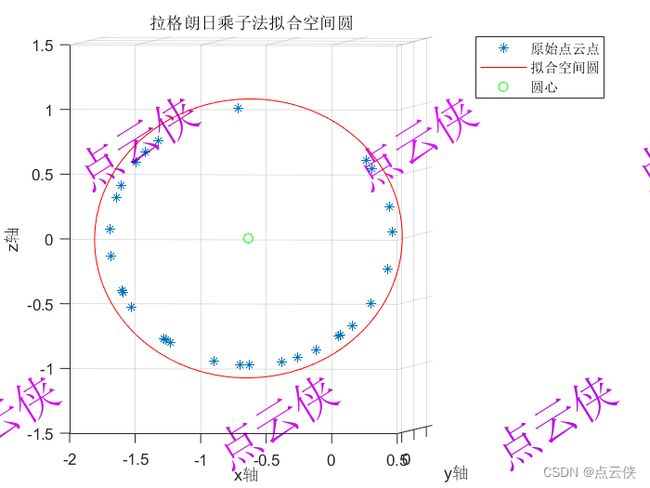
最小二乘拟合空间圆——拉格朗日乘子法
目录
- 一、拉格朗日乘子法
- 二、空间圆拟合
-
- 2.1、建立空间圆方程
- 2.2、构建Lagrange目标函数
- 2.3、求解圆心和半径
- 2.4、参考文献
- 三、算法伪码
- 四、算法效果
一、拉格朗日乘子法
拉格朗日乘子法又称为拉格朗日乘数法,用来求解函数 f ( x 1 , x 2 , . . . ) f(x_1,x_2,...) f(x1,x2,...)在 g ( x 1 , x 2 , . . . ) = 0 g(x_1,x_2,...)=0 g(x1,x2,...)=0的约束条件下的极值。拉格朗日乘子法一般分为3个步骤:首先,引入一个新的参数λ(称为拉格朗日乘子);其次,联立约束条件及原函数,使得变量数量与方程数量相同;最后,求出方程中各个变量的解。拉格朗日乘子法在微分几何、数学物理方程中有着重要应用,同时在经济学及工程学等实际领域中也有着广泛的应用。
二、空间圆拟合
传统方法并非直接对空间圆弧进行拟合,其拟合精度易受噪声影响且鲁棒性差。因此,在拉格朗日乘子法的基础上,基于平面条件约束建立目标函数,进而推导出空间圆弧拟合方程。
基于拉格朗日乘子法的空间圆弧拟合步骤如下:
2.1、建立空间圆方程
{ A x + B y + C z + D = 0 ( x - x 0 ) 2 + ( y - y 0 ) 2 + ( z - z 0 ) 2 = R 2 (1) \begin{cases} Ax + By + Cz + D = 0\\ (x - x_0)^ 2 + ( y - y_0)^ 2 + ( z - z_0)^ 2 = R^2 \end{cases} \tag{1} {Ax+By+Cz+D=0(x-x0)2+(y-y0)2+(z-z0)2=R2(1)
式中: A x + B y + C z + D = 0 Ax + By + Cz + D = 0 Ax+By+Cz+D=0表示一个法向量为 ( A , B , C ) (A,B,C) (A,B,C)的平面方程;
( x - x 0 ) 2 + ( y - y 0 ) 2 + ( z - z 0 ) 2 = R 2 (x - x_0)^ 2 + ( y - y_0)^ 2 + ( z - z_0)^ 2 = R^2 (x-x0)2+(y-y0)2+(z-z0)2=R2表示球心坐标为: ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0)、半径为 R R R的球面方程。
然后,通过三维数据点建立空间平面方程:
[ x 1 y 1 z 1 1 x 2 y 2 z 2 1 ⋮ ⋮ ⋮ 1 x n y n z n 1 ] [ A B C D ] = [ 0 0 ⋮ 0 ] (2) \left[ \begin{matrix} x_1&y_1&z_1&1 \\ x_2&y_2&z_2 &1\\ \vdots &\vdots &\vdots &1\\ x_n&y_n&z_n&1 \\ \end{matrix} \right] \left[ \begin{matrix} A \\ B\\ C\\ D\\ \end{matrix} \right]= \left[ \begin{matrix} 0 \\ 0 \\ \vdots \\ 0\\ \end{matrix} \right] \tag{2} x1x2⋮xny1y2⋮ynz1z2⋮zn1111 ABCD = 00⋮0 (2)
式中: ( x 1 , y 1 , z 1 ) (x_1,y_1,z_1) (x1,y1,z1)、 ( x 2 , y 2 , z 2 ) (x_2,y_2,z_2) (x2,y2,z2)、…、 ( x n , y n , z n ) (x_n,y_n,z_n) (xn,yn,zn)为三维数据点。
根据式(2),利用最小二乘法拟合得到平面方程的系数 A 、 B 、 C 、 D A、B、C 、D A、B、C、D,进而可得出空间圆所在空间的平面方程。将全部点云数据 ( x i , y i , z i ) (x_i,y_i,z_i) (xi,yi,zi)投影到平面 A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0上,得到投影点 ( x i ′ , y i ′ , z i ′ ) (x_i^{'},y_i^{'},z_i^{'}) (xi′,yi′,zi′),各点投影公式为:
{ x i ′ = A ⋅ k + x i y i ′ = A ⋅ k + y i z i ′ = A ⋅ k + z i (3) \begin{cases} x_{i}^{'}=A\cdot k+x_{i}\\ y_{i}^{'}=A\cdot k+y_{i}\\ z_{i}^{'}=A\cdot k+z_{i}\\ \end{cases} \tag{3} ⎩ ⎨ ⎧xi′=A⋅k+xiyi′=A⋅k+yizi′=A⋅k+zi(3)
式中, k = − A x i + B y i + C z i + D A 2 + B 2 + C 2 k=-\frac{Ax_i+By_i+Cz_i+D}{A^2+B^2+C^2} k=−A2+B2+C2Axi+Byi+Czi+D
2.2、构建Lagrange目标函数
由解析几何知识可得,投影点 ( x i ′ , y i ′ , z i ′ ) (x_i^{'},y_i^{'},z_i^{'}) (xi′,yi′,zi′)定是平面与球面的相交点,可利用最小二乘法进行求解。将空间圆方程组当作一个多元函数条件极值问题,引入新的参数 λ λ λ(拉格朗日乘子),构建Lagrange目标函数:
F ( x 0 , y 0 , z 0 , R , λ ) = ∑ i = 1 n [ ( x i ′ − x 0 ) 2 + ( y i ′ − y 0 ) 2 + ( z i ′ − z 0 ) 2 − R 2 ] 2 + λ ( A x 0 + B y 0 + C z 0 + D ) (4) F(x_0,y_0,z_0,R,λ)=\sum_{i=1}^n[\ (x_{i}^{'}-x_0)^2+(y_{i}^{'}-y_0)^2+(z_{i}^{'}-z_0)^2-R^2]^2\\+λ(Ax_0+By_0+Cz_0+D)\tag{4} F(x0,y0,z0,R,λ)=i=1∑n[ (xi′−x0)2+(yi′−y0)2+(zi′−z0)2−R2]2+λ(Ax0+By0+Cz0+D)(4)
进而根据极值条件建立方程组:
F x 0 ′ = F y 0 ′ = F z 0 ′ = F R 0 ′ = F λ ′ = 0 (5) F_{x_0}^{'}=F_{y_0}^{'}=F_{z_0}^{'}=F_{R_0}^{'}=F_{λ}^{'}=0\tag{5} Fx0′=Fy0′=Fz0′=FR0′=Fλ′=0(5)
联立方程进行求解。
在解方程组过程中假设式(6)成立:
( x i ′ − x 0 ) 2 + ( y i ′ − y 0 ) 2 + ( z i ′ − z 0 ) 2 − R 2 ≈ 0 (6) \ (x_{i}^{'}-x_0)^2+(y_{i}^{'}-y_0)^2+(z_{i}^{'}-z_0)^2-R^2\approx0\tag{6} (xi′−x0)2+(yi′−y0)2+(zi′−z0)2−R2≈0(6)
然后消去多项式中的高次项,从而获得计算圆心坐标与半径的参数方程,如式(7)所示:
[ 8 M − 4 N T O T 2 N U 0 0 0 0 ] X = T (7) \left[ \begin{matrix} 8M&-4N^T&O^T \\ 2N&U&0 \\ 0 &0&0 \\ \end{matrix} \right] X=T \tag{7} 8M2N0−4NTU0OT00 X=T(7)
式中:
M = [ ∑ i = 1 n x i ′ 2 ∑ i = 1 n x i ′ y i ′ ∑ i = 1 n x i ′ z i ′ ∑ i = 1 n x i ′ y i ′ ∑ i = 1 n y i ′ 2 ∑ i = 1 n y i ′ z i ′ ∑ i = 1 n x i ′ z i ′ ∑ i = 1 n y i ′ z i ′ ∑ i = 1 n z i ′ 2 ] M= \left[ \begin{matrix} \sum_{i=1}^n\ x_{i}^{'2}&\sum_{i=1}^n\ x_{i}^{'}y_{i}^{'}&\sum_{i=1}^n\ x_{i}^{'}z_{i}^{'} \\ \sum_{i=1}^n\ x_{i}^{'}y_{i}^{'}&\sum_{i=1}^n\ y_{i}^{'2}&\sum_{i=1}^n\ y_{i}^{'}z_{i}^{'} \\ \sum_{i=1}^n\ x_{i}^{'}z_{i}^{'} &\sum_{i=1}^n\ y_{i}^{'}z_{i}^{'} &\sum_{i=1}^n\ z_{i}^{'2} \\ \end{matrix} \right] M= ∑i=1n xi′2∑i=1n xi′yi′∑i=1n xi′zi′∑i=1n xi′yi′∑i=1n yi′2∑i=1n yi′zi′∑i=1n xi′zi′∑i=1n yi′zi′∑i=1n zi′2
N = [ ∑ i = 1 n x i ′ ∑ i = 1 n y i ′ ∑ i = 1 n z i ′ ] N= \left[ \begin{matrix} \sum_{i=1}^n\ x_{i}^{'}&\sum_{i=1}^n\ y_{i}^{'}&\sum_{i=1}^n\ z_{i}^{'} \\ \end{matrix} \right] N=[∑i=1n xi′∑i=1n yi′∑i=1n zi′]
O = [ ∑ i = 1 n A ∑ i = 1 n B ∑ i = 1 n C ] O= \left[ \begin{matrix} \sum_{i=1}^n\ A&\sum_{i=1}^n\ B&\sum_{i=1}^n\ C \\ \end{matrix} \right] O=[∑i=1n A∑i=1n B∑i=1n C]
U = ∑ i = 1 n ( − 1 ) U=\sum_{i=1}^n\ (-1) U=i=1∑n (−1)
X = [ x 0 y 0 z 0 l λ ] X= \left[ \begin{matrix} x_0&y_0&z_0&l&λ\end{matrix} \right] X=[x0y0z0lλ]
T = [ 4 ∑ i = 1 n ( x i ′ 3 + x i ′ y i ′ 2 + x i ′ z i ′ 2 ) 4 ∑ i = 1 n ( y i ′ x i ′ 2 + y i ′ 3 + y i ′ z i ′ 2 ) 4 ∑ i = 1 n ( z i ′ x i ′ 2 + z i ′ y i ′ 2 + z i ′ 3 ) ∑ i = 1 n ( x i ′ 2 + y i ′ 2 + z i ′ 2 ) ∑ i = 1 n ( − D ) ] T= \left[ \begin{matrix} 4\sum_{i=1}^n\ (x_{i}^{'3}+ x_{i}^{'}y_{i}^{'2}+ x_{i}^{'}z_{i}^{'2})\\ 4\sum_{i=1}^n\ (y_{i}^{'}x_{i}^{'2}+y_{i}^{'3}+ y_{i}^{'}z_{i}^{'2})\\ 4\sum_{i=1}^n\ (z_{i}^{'}x_{i}^{'2}+ z_{i}^{'}y_{i}^{'2}+z_{i}^{'3})\\ \sum_{i=1}^n\ (x_{i}^{'2}+ y_{i}^{'2}+z_{i}^{'2})\\ \sum_{i=1}^n\ (-D)\\ \end{matrix} \right] T= 4∑i=1n (xi′3+xi′yi′2+xi′zi′2)4∑i=1n (yi′xi′2+yi′3+yi′zi′2)4∑i=1n (zi′xi′2+zi′yi′2+zi′3)∑i=1n (xi′2+yi′2+zi′2)∑i=1n (−D)
2.3、求解圆心和半径
将式(3)中的投影点 ( x i ′ , y i ′ , z i ′ ) (x_i^{'},y_i^{'},z_i^{'}) (xi′,yi′,zi′)代入方程(6),进而得到空间圆的圆心坐标和 l l l值,将圆心坐标代入 l = x 0 2 + y 0 2 + z 0 2 − R 2 l=x_{0}^2+y_{0}^2+z_{0}^2-R^2 l=x02+y02+z02−R2 即可解出空间圆的半径 R R R。
2.4、参考文献
[1] 化春键,熊雪梅,陈莹.基于拉格朗日乘子法的空间圆弧拟合优化方法[J].工程设计学报,2018,25(06):661-667.
三、算法伪码
%% -------------------------------读取点云---------------------------------
pc = PointCloudReader('Circle.pcd');
%% ------------------------------PCA拟合平面-------------------------------
coeff = pcaFitPlane(pc);
% 获取最小特征值对应的特征向量
A = coeff(1);
B = coeff(2);
C = coeff(3);
% 计算原点到拟合平面的距离
centroid = mean(pc);
D = -dot(A B C,centroid);
%% ----------------------------投影到拟合平面------------------------------
x' = x*(B * B + C * C) - A * (y*B + z.*C + D)/norm([A,B,C]);
y' = y*(A * A + C * C) - B * (x*A + z*C + D)/norm([A,B,C]);
z' = z*(A * A + B * B) - C * (x*A + y*B + D)/norm([A,B,C]);
%% -------------------------拉格朗日乘子法拟合圆---------------------------
% 构建U所需的元素
U = -1*n;
% 构建矩阵T所需的元素
sumE = sum(x'^3 + x'*y'*y' + x'*z'*z');
sumF = sum(y'*x'*x' + y'^3 + y'*z'*z');
sumG = sum(z'*x'*x' + z'*y'*y' + z'^3);
sumH = sum(x'^2 + y'^2 + z'^2);
sumI = -D*n;
% 矩阵M
M = [sumXX sumXY sumXZ;
sumXY sumYY sumYZ;
sumXZ sumYZ sumZZ];
% 矩阵N
N = [sumX sumY sumZ];
% 矩阵O
O = [sumA sumB sumC];
% 矩阵T
T = [4*sumE 4*sumF 4*sumG sumH sumI]';
% 系数矩阵W
W = [8 * M -4 * N' O' 2 * N U];
% 最小二乘求解
X = W\T;
% 空间圆半径
r = sqrt(norm(X(1:3))-X(4));
% 空间圆圆心
center = X(1:3);
%% ------------------------输出空间圆的拟合参数---------------------------
fprintf('圆的半径为: %f\n', r);
fprintf('圆心坐标为: ');
center
fprintf('圆法向量为:');
[A,B,C]
%% ----------------------------结果可视化----------------------------------
figure
% 1、绘制原始点
h1 = plot3(x, y, z, '*');
% 2、绘制拟合空间圆
theta = (0:2 * pi / 100 : 2 * pi)'; % theta角从0到2*pi
a = cross([A B C], [1 0 0]); % X与i叉乘,求取a向量
if ~any(a) % 如果a为零向量,将X与[0 1 0]叉乘
a = cross([A B C], [0 1 0]);
end
b = cross([A B C], a);% 求取b向量
a = a / norm(a); % 单位化a向量
b = b / norm(b); % 单位化b向量
c1 = center(1) * ones(size(theta, 1), 1);
c2 = center(2) * ones(size(theta, 1), 1);
c3 = center(3) * ones(size(theta, 1), 1);
x = c1 + r * a(1) * cos(theta) + r * b(1) * sin(theta);% 圆上各点的x坐标
y = c2 + r * a(2) * cos(theta) + r * b(2) * sin(theta);% 圆上各点的y坐标
z = c3 + r * a(3) * cos(theta) + r * b(3) * sin(theta);% 圆上各点的z坐标
hold on;
h2 = plot3(x, y, z, '-r');
% 3、绘制拟合圆圆心
h3 = plot3(center(1),center(2),center(3),'go');
xlabel('x轴')
ylabel('y轴')
zlabel('z轴')
legend([h1 h2 h3], '原始点云点', '拟合空间圆', '圆心');
title("拉格朗日乘子法拟合空间圆")
grid on