2023年美赛A题赛后总结
文章目录
- 心路历程
-
- 1. 选题
- 2. 初次建模
- 3. 数据收集
- 4. 二次建模
- 5. 算法实现以及优化
- 6.全英论文撰写
- 总结
心路历程
2023年美赛是在2月17号早上6点到2月21号早上8点这期间举行的,美赛开赛前一天我们三个人还在考期末考,甚至美赛刚开始前两天有位队友每天还要考一科,所以整体时间并不充裕。
我们三个人其实并没有特别明确的分工,可能每个部分三个人都参与了一些,我和一位同学主要参与数学建模和算法实现以及优化,另外一位主要写英文论文。我们作为美赛小白,第一次打美赛也是经验不足,所以以下美赛回顾仅供参考。
1. 选题
第一天早上我们其中一位同学要考试,所以我和主要写论文的同学将题目翻译浏览了一遍,还把其中的关键词画了出来,翻译软件推荐deepl。我们首先排掉了B、D和F题,因为我们不太擅长像F这样的政策题,D题指标太明确对我们不是很有利,B题太泛了没啥思路。我们又在A、C、E三道题中纠结,我们接着排掉C题,C题太具体没有发挥空间,不利于创新。后面又排掉E题,因为对这个知识背景不算了解感觉E题数据不好找,最后权衡下选择了A题(结果被A题找数据难住了,找了大半天愣是没找到A题有用的数据)。
2. 初次建模
初次建模是我们还没有找好数据,经过我们对题目的分析和讨论,和大量的文献查阅(推荐知网和谷歌学术),主要确立了两大类模型:单种群模型和多种群模型。总体的解决题目所提出的问题的思路是:
1、收集几个干旱地区降水量在某段时间变化的数据,通过线性回归或者差分自回归移动平
均模型对降水量进行拟合和预测,最后将用干旱指标SPI来衡量;
2、收集对应几个干旱地区植物物种的一些指标随这段时间变化的数据,这些指标包括植物物种种类数、对应的每个植物物种的密度、植物多样性指数、对应的每个植物物种的生长率,其实这些指标最后都可以通过生物量和物种种类数转化计算出来。收集完这些数据并转化为指标后要用到时间序列预测模型对指标变化进行预测,差分自回归移动平均模型和LSTM模型都行,根据数据样本量决定
3、使用熵权法对指标的数据进行综合衡量,最后得出一个综合评分用于衡量对应时间的天气变化对群落的影响和衡量群落的受益程度,注意该评分也是随时间变化的评分,该评分也会随地区物种种类数发生变化。注意收集到的几个干旱地区一定要在物种种类数上有区别,我们刚开始考虑的是收集一个物种、五个物种、十几个物种的干旱地区的数据(其实过于理想化,最后真的找不到相关数据)
4、简单建立一个基于Lotka-Volterra的种群竞争模型,分析一下物种间的相互作用来回答物种类型对群落影响的问题
5、最后还要收集污染和栖息地的随时间变化的相关数据,生成一个环境破坏的指标
刚开始总体建模我们没有采用多元分析的方法,而是利用控制变量和分类讨论的思想对时间序列数据按照干旱指标、物种种类数、环境破坏的指标进行对比分析。总体来说如果数据到位我们基本能回答题目要求的问题而且比较具体真实,但是模型缺乏泛化能力,因为数据总是片面的。
3. 数据收集
这次数据收集是美赛的一大难点,除了C题基本上数据都不好找,A题数据尤为难找。这里先推荐一些地理生物类数据收集网站,例如知网、每个国家的地理所、美国农业部等(其实可以试试ChatGPT,有时它会告诉你一些收集数据的网站)。最后我们的其他两位组员找了一天多只找到几个干旱地区降水量在某段时间变化的数据(科尔沁沙地),虽然有某个固定时间的植物物种数据,但怎么找都没有植物物种随时间变化的数据,可能也没啥人去统计这个,最后决定大改模型。
2008-2017天童演替系列样地数据集
4. 二次建模
由于找不到合适的数据,经过我和队友讨论后,我们一致认为A题的核心不在于找数据,而在于从机理分析的角度去分析种群的增长。机理分析建模是通过对系统内部原因(机理)的分析研究,从而找出其发展变化规律的一种科学研究方法。查阅了大量有关种群增长的文献后,我们抽象出两大类种群模型:
1、基于logistics方程的单物种增长的微分方程模型,其中我们考虑了天气因子并将转化为降水量对植物生长率的影响,还考虑了自抑制系数,即物种内部每个个体在抢占资源时的互相抑制作用。其中 h ( t ) h(t) h(t) 是关于降水量的函数, r r r 是物种增长潜力指数, N N N 是物种的生物量, k k k 是环境最大容量, θ \theta θ 是自抑制系数, u u u 是物种规模
d u d t = 1 1 + e − ∇ k ∗ h ( t ) ∗ ( 1 − θ u ) ∗ u \frac{du}{dt} = \frac{1}{1 + e^{-\nabla k *h(t)}} * (1- \theta u) * u dtdu=1+e−∇k∗h(t)1∗(1−θu)∗u
∇ k = r ∗ N ∗ ( k − N ) k \nabla k = \frac{r*N*(k-N)}{k} ∇k=kr∗N∗(k−N)
2、基于Lotka-Volterra的多物种种群竞争微分方程模型,除了考虑了天气因子和自抑制系数,还考虑了物种间竞争系数,该系数利用判断矩阵来衡量,即物种 i i i 比物种 j j j 竞争能力强则向矩阵填入2,相等则填入1,弱则填入1/2。其中 L i L_{i} Li 是物种最大生长率, β \beta β 是物种相互作用系数
d u i d t = ( L i 1 + e − ∇ k ∗ h ( t ) − L i 2 ) ∗ ( 1 − θ u i − ∑ i ≠ j n β u j ) ∗ u i \frac{du_{i}}{dt} =( \frac{L_{i}}{1 + e^{-\nabla k *h(t)}} - \frac{L_{i}}{2}) * (1- \theta u_{i} - \sum_{i \ne j}^n \beta u_{j} ) * u_{i} dtdui=(1+e−∇k∗h(t)Li−2Li)∗(1−θui−i=j∑nβuj)∗ui
3、参考文献我们额外建立了一个环境污染的种群动力学微分方程模型并加入到多物种模型中,而不是将污染指标单独作为一个系数或者将环境破环指标用熵权法得出一个综合系数。其中。 C 0 ( t ) C_{0}(t) C0(t) 是t时刻生物体内的毒素浓度, C E ( t ) C_{E}(t) CE(t)是t时刻环境中的毒素浓度, r i 0 r_{i0} ri0 表示第 i i i 个种群在没有毒素的影响下增长率, r i 1 r_{i1} ri1表示体内的毒素对第i个种群的剂量反应系数, K K K 是生物对环境中毒素的摄取率, h h h 是环境中毒素的稀释净化率, g g g 是被其他生物净化的生物体内毒素, m m m 是生物体内毒素的净化率, 环境中毒素的排放用函数 u ( t ) u(t) u(t) 来表示。
d u i d t = ( L i 1 + e − ∇ k ∗ h ( t ) − L i 2 ) ∗ ( 1 + r i 0 − r i 1 C 0 ( t ) − θ u i − ∑ i ≠ j n β u j ) ∗ u i \frac{du_{i}}{dt} =( \frac{L_{i}}{1 + e^{-\nabla k *h(t)}} - \frac{L_{i}}{2}) * (1 + r_{i0} - r_{i1}C_{0}(t)- \theta u_{i} - \sum_{i \ne j}^n \beta u_{j} ) * u_{i} dtdui=(1+e−∇k∗h(t)Li−2Li)∗(1+ri0−ri1C0(t)−θui−i=j∑nβuj)∗ui
d C 0 ( t ) d t = K C E ( t ) − ( g + m ) C 0 ( t ) \frac{dC_{0}(t)}{dt} = KC_{E}(t) - (g+m)C_{0}(t) dtdC0(t)=KCE(t)−(g+m)C0(t)
d C E ( t ) d t = − h C E ( t ) + u ( t ) \frac{dC_{E}(t)}{dt} = -hC_{E}(t) + u(t) dtdCE(t)=−hCE(t)+u(t)
这就是我们二次建模的总体框架,虽然有些制约因素考虑仍然欠缺,不过我们将制约因素的重点都抽象成数学表达式,为算法和代码提供可解的基石。
5. 算法实现以及优化
写代码时我们用的是Python,拓展性比较强,但会用matlab的建议还是用matlab。写代码的总体思路其实就是将上述微分方程用numpy和scipy库求解,并用matplotlib做可视化,极力推荐plotly做绘图与可视化,它可以画更多美丽高级的图。既然没有数据,那写完代码调参这一块就尤为重要,调参时要自己衡量一下最后的结果是否合理并能解释的通,还有就是数据可视化时我们采用的是控制变量的对比分析法来评价不同参数的变化对种群规模的影响,所以一副子图中要有至少两幅以上的图片来做对比说明,代码比较多这里就不一一展示了。
from scipy.integrate import odeint # 导入 scipy.integrate 模块
import numpy as np # 导入 numpy包
import matplotlib.pyplot as plt # 导入 matplotlib包
def dyLV5(y, t, r, k, l,m, a, b, c,d,e): # 5物种LK模型
u1, u2, u3 ,u4 ,u5 = y
du1_dt = (l/2-l / (1 + np.exp((-4*t+180) * r / k * u1 * (k - u1)))) * u1 * (
10 - m * u1 - b/a * u2 - c/a * u3 - d/a*u4 - e/a* u5 )
du2_dt = (l/2-l / (1 + np.exp((-4*t+180) * r / k * u2 * (k - u2)))) * u2 * (
10 - a/b * u1 - m * u2 - c/b * u3 - d/b*u4 - e/b* u5 )
du3_dt = (l/2-l / (1 + np.exp((-4*t+180) * r / k * u3 * (k - u3)))) * u3 * (
10 - a/c * u1 - b/c * u2 - m * u3 - d/c*u4 - e/c* u5 )
du4_dt = (l/2-l / (1 + np.exp((-4*t+180) * r / k * u4 * (k - u4)))) * u4 * (
10 - a/d * u1 - b/d * u2 - c/d * u3 - m*u4 - e/d* u5 )
du5_dt = (l/2-l / (1 + np.exp((-4*t+180) * r / k * u5 * (k - u5)))) * u5 * (
10 - a/e * u1 - b/e * u2 - c/e * u3 - d/e*u4 - m* u5 )
return np.array([du1_dt, du2_dt, du3_dt,du4_dt, du5_dt])
Matrix = [[1,1/2,1/2,1/2,1/2],[2,1,1/2,1/2,2],[2,2,1,2,2],[2,2,1/2,1,2],[2,1/2,1/2,1/2,1]]
Matrix1 = [[1,1/2,1/2,1/2,2],[2,1,2,2,2],[2,1/2,1,2,2],[2,1/2,1/2,1,2],[1/2,1/2,1/2,1/2,1]]
def func2(Matrix):
M = np.array(Matrix) # a为自己构造的输入判别矩阵
w = np.linalg.eig(M) # np.linalg.eig(matri)返回特征值和特征向量
value_max = np.max(w[0]) # 最大特征值
t = np.argwhere(w[0] == value_max) # 寻找最大特征值所在的行和列
vector_max = w[1][::-1, t[0]]# 最大特征值对应的特征向量
return (value_max)
data_value_max=func2(Matrix)
print(data_value_max)
print('\n')
def func3(Matrix,value_max):
RI_list = [0, 0, 0.58, 0.9, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49, 1.52, 1.54, 1.56, 1.58, 1.59]
M = np.array(Matrix)
n = M.shape[0]
RI = RI_list[n]
CI = (value_max - n) / (n - 1)
CR = CI / RI
print(CR)
if CR < 0.1:
print("通过一致性检验")
else:
print("没有通过一致性检验")
func3(Matrix,data_value_max)
def func4(Matrix):
M = np.array(Matrix)
S = M.shape
M_p = np.zeros(S[0]*S[1]).reshape(S[0],S[1])
M_add = np.zeros(S[0]).reshape(S[0],1)
for n in range(S[0]):
for m in range(S[1]):
M_p[n][m] = M[n][m]/M[:,m].sum()
print(M_p)
print('\n')
for k in range(S[0]):
M_add[k][0] = M_p[k,:].sum()/S[1]
M_add = M_add.reshape(S[1])
print('\n')
return(M_add)
M=func4(Matrix)
M1=func4(Matrix1)
# 设置模型参数
a, b ,c ,d ,e= M
a1, b1 ,c1 ,d1 ,e1= M1
r, k, l ,m= 1.1, 1, 1, 0.08
tEnd1 = 3 # 预测长度
tEnd2 = 3 # 预测长度
t1 = np.arange(0.0, tEnd1, 0.1) # (start,stop,step)
t2 = np.arange(0.0, tEnd2, 0.1) # (start,stop,step)
u10, u20, u30,u40, u50= 0.15,0.2,0.25,0.3,0.1 # 初值
u101, u201, u301,u401, u501= 0.15,0.2,0.25,0.3,0.1 # 初值
Y0 = (u10, u20, u30,u40, u50) # 微分方程组的
Y1 = (u101, u201, u301,u401, u501)
# plt.subplot(121), plt.title("1. u(r)")
yt = odeint(dyLV5, Y0, t1, args=(a, b, c,d,e, r, k, l,m)) # SIS 模型
# SIS 模型
M1 = np.trunc(yt[0] * 100).astype(int)
M2 = np.trunc(yt[3] * 100).astype(int)
M3 = np.trunc(yt[6] * 100).astype(int)
M4 = np.trunc(yt[14] * 100).astype(int)
x1 = 50
y1 = 50
print(M1)
print(M2)
print(M3)
print(M4)
M1_x = np.zeros(M1[0] + M1[1] + M1[2] + M1[3])
M1_y = np.zeros(M1[0] + M1[1] + M1[2] + M1[3])
for i in range(M1[0]):
M1_x[i] = 50 * np.random.rand(1)
M1_y[i] = 50 * np.random.rand(1)
for i in range(M1[1]):
M1_x[i+M1[0]] = 50 * np.random.rand(1) + 50
M1_y[i+M1[0]] = 50 * np.random.rand(1)
for i in range(M1[2]):
M1_x[i+M1[0]+M1[1]] = 50 * np.random.rand(1)
M1_y[i+M1[0]+M1[1]] = 50 * np.random.rand(1) +50
for i in range(M1[3]):
M1_x[i+M1[2]+M1[0]+M1[1]] = 50 * np.random.rand(1) + 50
M1_y[i+M1[2]+M1[0]+M1[1]] = 50 * np.random.rand(1) + 50
M2_x = np.zeros(M2[0] + M2[1] + M2[2] + M2[3])
M2_y = np.zeros(M2[0] + M2[1] + M2[2] + M2[3])
for i in range(M2[0]):
M2_x[i] = 50 * np.random.rand(1)
M2_y[i] = 50 * np.random.rand(1)
for i in range(M2[1]):
M2_x[i+M2[0]] = 50 * np.random.rand(1) + 50
M2_y[i+M2[0]] = 50 * np.random.rand(1)
for i in range(M2[2]):
M2_x[i+M2[0]+M2[1]] = 50 * np.random.rand(1)
M2_y[i+M2[0]+M2[1]] = 50 * np.random.rand(1) + 50
for i in range(M2[3]):
M2_x[i+M2[2]+M2[0]+M2[1]] = 50 * np.random.rand(1) + 50
M2_y[i+M2[2]+M2[0]+M2[1]] = 50 * np.random.rand(1) + 50
M3_x = np.zeros(82)
M3_y = np.zeros(82)
for i in range(M3[0]):
M3_x[i] = 50 * np.random.rand(1)
M3_y[i] = 50 * np.random.rand(1)
for i in range(M3[1]):
M3_x[i+M3[0]] = 50 * np.random.rand(1) + 40
M3_y[i+M3[0]] = 50 * np.random.rand(1)
for i in range(M3[2]):
M3_x[i+M3[1]+M3[0]] = 50 * np.random.rand(1)
M3_y[i+M3[1]+M3[0]] = 50 * np.random.rand(1) + 50
for i in range(M3[3]):
M3_x[i+M3[2]+M3[1]+M3[0]] = 50 * np.random.rand(1) + 50
M3_y[i+M3[2]+M3[1]+M3[0]] = 50 * np.random.rand(1) + 50
M4_x = np.zeros(83)
M4_y = np.zeros(83)
for i in range(M4[0]):
M4_x[i] = 50 * np.random.rand(1)
M4_y[i] = 50 * np.random.rand(1)
for i in range(M4[1]):
M4_x[i+M4[0]] = 50 * np.random.rand(1) + 50
M4_y[i+M4[0]] = 50 * np.random.rand(1)
for i in range(M4[2]):
M4_x[i+M4[0]+M4[1]] = 50 * np.random.rand(1)
M4_y[i+M4[0]+M4[1]] = 50 * np.random.rand(1) + 50
for i in range(M4[3]):
M4_x[i+M4[2]+M4[0]+M4[1]] = 50 * np.random.rand(1) + 50
M4_y[i+M4[2]+M4[0]+M4[1]] = 50 * np.random.rand(1) + 50
colors1 = []
colors2 = []
colors3 = []
colors4 = []
plt.figure(figsize=(30, 30))
for x, y in zip(M1_x, M1_y):
if y >= y1:
if x > x1:
colors1.append('orange')
else:
colors1.append('blue')
else:
if x <= x1:
colors1.append('purple')
else:
colors1.append('green')
for x, y in zip(M2_x, M2_y):
if y > y1:
if x > x1:
colors2.append('orange')
else:
colors2.append('blue')
else:
if x < x1:
colors2.append('purple')
else:
colors2.append('green')
for x, y in zip(M3_x, M3_y):
if y > y1:
if x > x1:
colors3.append('orange')
else:
colors3.append('blue')
else:
if x < x1:
colors3.append('purple')
else:
colors3.append('green')
for x, y in zip(M4_x, M4_y):
if y > y1:
if x > x1:
colors4.append('orange')
else:
colors4.append('blue')
else:
if x < x1:
colors4.append('purple')
else:
colors4.append('green')
plt.subplot(221)
plt.scatter(M1_x, M1_y , marker='o', c=colors1 )
plt.rcParams.update({'font.size': 20})
plt.legend(loc="lower left", title ="t = 0")
plt.subplot(222)
plt.scatter(M2_x,M2_y , marker='o', c=colors2)
plt.legend(loc="lower left", title="t = 3")
plt.subplot(223)
plt.scatter(M3_x,M3_y , marker='o', c=colors3)
plt.legend(loc="lower left", title="t = 6")
plt.subplot(224)
plt.scatter(M4_x,M4_y ,marker='o', c=colors4)
plt.legend(loc="lower left", title="t = 14")
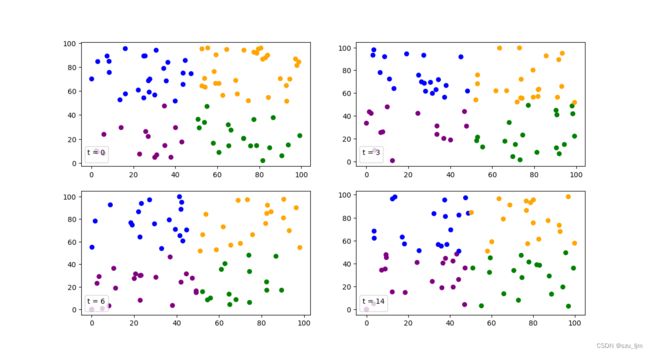
plt.show()
无污染下的四个物种的种群竞争图
6.全英论文撰写
全英论文的撰写我主要参与了摘要部分,摘要是最重要的一部分,摘要写得好能大大提高你的获奖概率,所以摘要一定要认真写,先直击主题和问题背景,然后直接上模型,模型要概括要点并说明解决了哪些问题,然后夸一下自己模型的优点,比如泛化能力强、考虑比较周全、模型精度高等
总结
以上就是2023美赛赛后总结,写的比较简陋,只是一些个人的回顾和心声,希望对小伙伴们有所帮助,愿所有打美赛的小伙伴们都能收获满满,在打比赛过程中增强自己的综合能力。