链表相关算法-反转链表、合并链表等
每天记录LeetCode的点点滴滴:day1-9.8
Question-反转链表
反转链表是很经典的算法题,解题的思路通常为数据结构里的栈,因为栈的特性是先进先出,所以在这个过程中我们遍历链表并将它压入栈中,就能实现问题的要求,同时满足题目所要求O(n)的时间复杂度;而如果要实现O(1)的空间复杂度的话就需要我们利用当前的链表空间,而不能新建。下面我将给出我所写的代码(同时包含改进版本)来进行记录。
版本一:
import java.util.*;
/*
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}*/
public class Solution {
public ListNode ReverseList(ListNode head) {
ListNode p = head, q, t;
//1. 链表判空操作
if(p == null){
return null;
}
//2.首先建立一个栈,利用栈先进后出的特性来进行链表的反转
Stack<ListNode> stack = new Stack<>();
//3.遍历链表,把链表加入到栈中
while(p != null){
q = p;
p = p.next;
stack.push(q);
}
//4.由于栈到空间复杂度要是O(n),故而利用当前度空间head来进行存储,先初始化head
head = null;
head = stack.pop();
t = head;
head.next = null;
//5.通过尾插法将栈中的节点取出
while(!stack.empty()){
q = stack.pop();
head.next = q;
head = q;
head.next = null;
}
return t;
}
}
虽然成功实现,但是觉得代码十分冗余,所以思考能不能对代码再进行优化。
版本二:
//1. 链表判空操作
if(head == null){
return null;
}
//2.初始化表头
ListNode cur = head, pre;
head = null;
//3.利用头插法来进行链表的逆转
while(cur != null){
pre = cur;
cur = cur.next;
pre.next = head;
head = pre;
}
return head;
相比第一次允许的情况,在时间上可能没有太大的改进,但是在空间上取得了巨大的进展,得益于我们将栈这一步优化掉,有栈的思想,但是不适用它,采用不带头节点的头插法来进行反转。
可能还有很多值得去改进的地方,现在自己也有任务在身,所以就尽最大努力就好,共勉!
每天记录LeetCode的点点滴滴:day2-9.10(补充昨天)
链表指定区间的反转,这个问题和第一题优点类似,区别在于一个是对整体一个是对部分,故而解题的思路是可以用将需要反转的区间部分当作是整体,最后再和其他链表的节点链接起来,这时候需要注意的是:要考虑到是否涉及头节点和非头节点的反转问题,如果涉及到头节点,不对其进行特殊处理的话,往往会导致错误,所以这个时候,可以通过引入虚拟头节点的方式来弥补这个缺陷。
解法
链解题的思路是:第一步创建一个虚拟头节点,并链接上需要处理的链表head;第二步是确定好边界,采用头插法的形式来反转链表,所以需要找到第m个节点的前一个节点,并且逐个删除节点至第n个;第三步即为对删除的节点进行头插法;最后返回虚拟节点的next节点,具体代码如下所示:
public static class ListNode {
int val;
ListNode next = null;
}
public static ListNode reverseBetween (ListNode head, int m, int n) {
//版本一:使用虚拟头节点,来处理涉及到头节点和非头节点的问题
ListNode zero = new ListNode();
//转变为zero为该链表的头节点
zero.next = head;
// 初始化
ListNode cur = zero, pre = zero, aft = null;
int count = 0;
while(count < m){
pre = cur;
cur = cur.next;
count++;
}
aft = cur.next;
//通过删除aft节点,并在pre节点中实施尾插法
while(count < n){
//删除aft节点
cur.next = aft.next;
//尾插法插入到pre节点后
aft.next = pre.next;
pre.next = aft;
aft = cur.next;
count++;
}
return zero;
}
每天记录Coding的点点滴滴:day3-9.11
1、问题
2、思路
想法是:每k组反转一次,这样的话,我们将整个链表看作是每k个一段,利用之前学的整个链表的反转以及反转部分链表进行操作。具体的步骤是(不是最优,是本身自己想到的觉得可行的想法):
- 判断要反转几组,通过遍历链表的方式
获取链表长度,然后➗k,等到需要反转的次数num; 设置loc、pre、cur以及aft四个节点,分别代表虚拟头节点、起到用来删除cur的前一个节点、当前要进行头插操作的节点、cur后一个节点(保证cur能正常的往后顺延);- 通过
删除cur、头插到loc、变换pre、cur以及aft的位置,反转num组之后就能实现该算法。
3、解法
import java.util.*;
// public class ListNode {
// int val;
// ListNode next = null;
// }
public class Solution {
/**
*
* @param head ListNode类
* @param k int整型
* @return ListNode类
*/
public ListNode reverseKGroup (ListNode head, int k) {
// write code here
//创建虚拟头节点
ListNode zero = new ListNode(-1);
zero.next = head;
ListNode loc = zero, pre = zero, cur = head, aft;
//判断需要反转几次
int num = 0;
int length = 0;
ListNode x = head;
while(x != null){
x = x.next;
length++;
}
num = length / k; //得到需要反转的次数
//判断在k内进行反转
int count = 1;
int countTime = 0;
while(countTime < num){
//取出需要反转的节点
pre.next = cur.next;
aft = pre.next;
//头插法
cur.next = loc.next;
loc.next = cur;
if(count == 1){
pre = loc.next;
}
//重定向cur
cur = aft;
//判断是否为一次完整的反转
if(count == k){
countTime++;
count = 0;
loc = pre;
}
count++;
}
return zero.next;
}
}
4、结果
day4-9.12
问题描述
思路
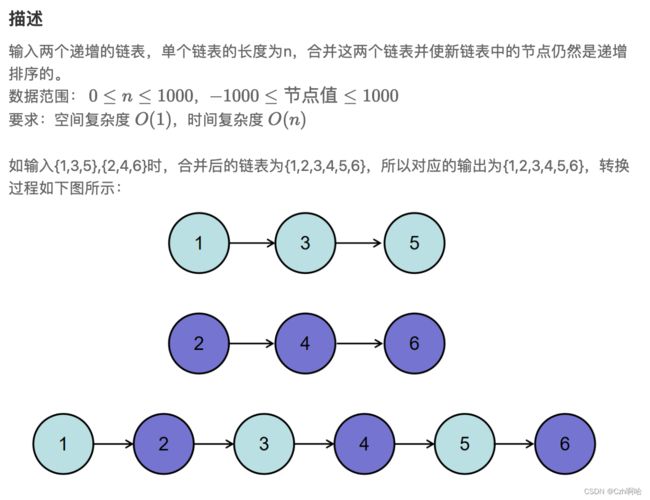
这是一道简单题,判断大小并进行插入,我自己的想法是,因为空间复杂度要为O(1),故而我们不能自己新建链表来将两个链表各自插入,所以采用的想法是:
- 确定返回的链表list1,每次判断list1和list2的当前值,并采用头插法的形式来进行插入,这时候需要注意的有,如果在第一次插入的时候list2的节点值小于list1的节点值,要对list2的节点进行删除操作,再将其插入到list1中,故而
引入虚拟头节点的概念。 - 知道大概的思路之后,剩下的步骤就是依次对list1和list2的节点进行比较,list1小的话
更新l1的位置和cur的位置即可,list2的节点小就需要删除、插入、更新三个部分,直到有l1或l2为空。 - 最后,要判断肯定是有某一个链表空,另外一个链表不为空,如l1为null,意味着list2有节点未处理完,
使用cur.next = zero2.next来把未处理的所有节点进行一次性插入,即链接链表;若是l1不为null,不需要处理,因为我们最终返回的是list1。不过这里需要注意的是,存在list1和list2全空的情况,所以要对if里的条件进行小小的处理:l1 == null && l2 != null - 结束!
代码
import java.util.*;
/*
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}*/
public class Solution {
public ListNode Merge(ListNode list1,ListNode list2) {
// 定义两个指针遍历链表,并且决定最终返回链表list1
ListNode l1 = list1, l2 = list2, cur;
// 创建一个虚拟节点,直接在该虚拟节点进行头插法即可
ListNode zero1 = new ListNode(-1);
zero1.next = list1;
cur = zero1;
ListNode zero2 = new ListNode(-1);
zero2.next = list2;
// 循环
while(l1 != null && l2 != null){
//比较大小
if(l1.val <= l2.val){
cur = l1;
l1 = l1.next;
}else{
// 删除
zero2.next = l2.next;
// 插入
l2.next = cur.next;
cur.next = l2;
cur = l2;
//更新l2
l2 = zero2.next;
}
}
// 判断现在list1或list2是空的
if(l1 == null && l2 != null){
cur.next = zero2.next;
}
return zero1.next;
}
}
结果
day5-9.13
1、问题描述
2、思路
这题的思路最开始的想法是这样的:
- 首先,观察题目,他没有具体的空间要求,所以我常见一个数组,然后遍历所有的链表,将链表节点的值依次存入到数组中。
- 其次,对数组进行sort排序。
- 最后,遍历数组,遍历的过程中新建节点,并插入到新的链表中并返回。
虽然上面的这个做法不是很优雅,但是不管黑猫白猫,只要能抓老鼠,就是好猫。又思考了另外的一种方法:
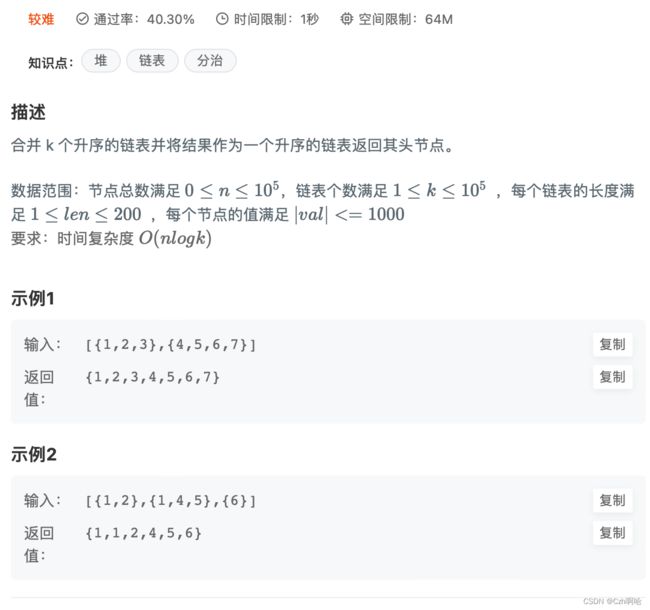
- 首先,先理清楚要怎么实现,多个链表,时间复杂度又要在O(nlogk),加上题目上的小提示,想到可以用分治法来实现,同样的在这个过程中有对链表进行两两合并,大概的情况是这样。
- 其次,实现
merge函数用来对两个链表进行合并,实现divideLists函数用来实现对链表的分治并连接,最后通过mergeKLists来实现这个问题。
3.注意⚠️:值得注意的是,在这个过程中比较难理解的是第二个函数divideLists,因为采用递归的思想:1)如果对函数的参数lists,left,right这三个,有left > right这显然是不对的,故而返回null;2)对left = right,这意味着当前lists区间只有一个函数,返回其中一个lists.get(left)或lists.get(right)都可以;3)最后是递归部分,该函数的最终目的是分治+链接,所以除上述两种情况,对该过程进行递归调用,merge(divide(lists,left,middle),divide(list,middle+1,right)),这个函数会进行不断的分治,直到出口left=right,再逐层进行merge,最后返回一个所有链表链接的新链表。
3、代码
import java.util.*;
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
//合并两个链表
public static ListNode merge(ListNode l1, ListNode l2){
//初始化
ListNode zero1 = new ListNode(0);
ListNode zero2 = new ListNode(0);
zero1.next = l1;
zero2.next = l2;
ListNode pre1 = zero1, cur1 = l1;
ListNode pre2 = zero2, cur2 = l2;
//遍历
while(cur1 != null && cur2 != null){
if(cur1.val <= cur2.val){
pre1 = cur1;
cur1 = cur1.next;
}else{
pre2.next = cur2.next;
//插入list1中
cur2.next = pre1.next;
pre1.next = cur2;
//更新pre1和cur2的位置
pre1 = cur2;
cur2 = pre2.next;
}
}
//判断l2是否为空,cur1为空的话无需处理
if(cur2 != null){
pre1.next = cur2;
}
return zero1.next;
}
//分治法的思想进行对lists的分割
public static ListNode divideLists(ArrayList<ListNode> lists, int left, int right){
//不存在这样的情况
if(left > right){
return null;
}else if(left == right){ //意味着只有一个listNode的链表,直接返回一个就行
return lists.get(left);
}
//从中间分隔开,采用低轨的思路进行连接
int middle = (left + right) / 2;
return merge(divideLists(lists, left, middle), divideLists(lists, middle+1, right));
}
//最终选择
public ListNode mergeKLists(ArrayList<ListNode> lists) {
return divideLists(lists, 0, lists.size()-1);
}
}
4、结果
day6-9.14
1、问题描述
可能刚开始有些人看到问题的时候会和我一样有点懵(也可能只有我比较笨),问题就是判断有没有环,这个输入不是就很明显了,那这个问题是在问什么,定睛一看原来输入只是解释而已。这个时候看到函数体只是输入了一个链表头节点,这就知道了问题所问!
2、思路
这道题的思路并不会很复杂,存在很多人都知道双指针,从同一起点出发,让两个指针保持不同的速度,如果存在环的话,那么定会有某时刻两个指针相遇;反之不存在环,那就会有指针为null,结束循环即可。
接下来我们就按照这个思路进行求解,不过在求解的过程中,可能会碰到一些小小的问题,就是空指针异常。较快的求法是:指针cur1和cur2同时指向head,然后让指针1以每次一步的速度前进,指针2以每次二步的速度前进,这样就能很好的判断。
值得注意的是,倘若在循环体里,cur2指向无环链表的最后一个节点,如果这时候再走两步的话,第一步是没问题的,cur2 = null,但是再走一步,就会导致null->next,报错!!!所以要在这边进行处理。

3、解题代码
import java.util.*;
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
/*
1.判断链表是否有环可以用两个指针,同时一前一后来出发
一个指针每次走一步,另外一个指针走两步,如果当走两
步的指针为null,说明链表是没有环的;如果指针1==指
针2,那么说明是有环的
*/
ListNode cur1 = head, cur2 = head;
while(cur2 != null){
cur1 = cur1.next;
cur2 = cur2.next;
if(cur2 == null){
return false;
}else{
cur2 = cur2.next;
}
if(cur1 == cur2){
return true;
}
}
return false;
}
}
4、总结
虽然这是一道easy题,但是其中存在的解题的思路和对边界值的思考还是值得我们好好去专研,fighting!!!

day7-9.15
1、问题描述
2、求解思路
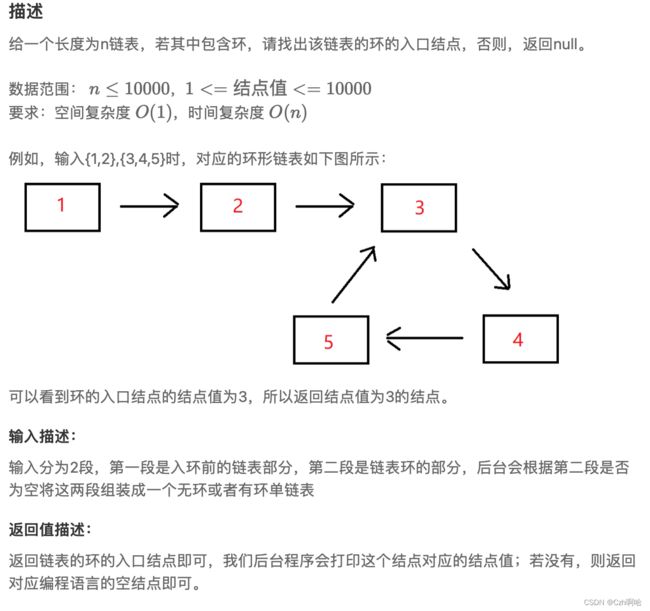
2.1、有环证明
针对这个问题,要求链表环的入口结点,那意味着这个链表可能存在环,昨天BM6没有对为什么双指针从相同位置出发,步长差1的速度前进,有环就必定为相遇,我们在今天做一个推导:
- 假设c1和c2同时从0出发,c1的速度为1,c2对速度为2;
- 由上图进行普通化,
路径长度为m,环的路径长度为n; - 我们假设他们在
k点相遇,距环入口为k,相遇的情况肯定是c2比c1多走了整数圈,假设c1为p圈,则c2为q圈,那么有:
1、关系
=>i = m + k + p * n;
=>2 * i = m + k + q * n;
2、化简
=> 2 * (m + k + p * n) = m + k + q * n
=> m + k = n * (q - 2p)
3、证明假设
只要存在某一组p、q、k存在,假设成立
令:p = 0,q = m,k = mn - m
有:m + mn - m = n * (m - 0)
即:mn = mn
故:假设成立
4、求i
此时,i = m + k + p * n
= m + mn - m + 0
= mn
5、假设成立
2.2、确定环入口的证明
前提:该链表存在环,并且与环中k处相遇,推导:
- 我们现在知道在某一时刻,c1和c2会相遇于k,那么接下来我们该怎么做!
- 由上一小节推出
m + k = n * (q - 2p)意味着m+k等于x倍的环长度,那么我们可以由此想,我们已经求得了c1和c2相遇的位置了,此位置到头节点的位置不正好m+k,那么会不会就联想到:
1、让其中一个节点回到头节点,假如让c1回去
c1 = pHead;
2、此时,是不是只要c1以每时刻一步的速度走m个时间段就能到达我们在上帝视角看到的环的入口结点;
3、同样的让c2也以每时刻一步的速度走m个时间段;
4、通过c2此时所处位置,我们可以知道如果以环的入口结点作为起点,c2走的路程为m+k,刚好是环长度n的x倍,即c2也走到了环入口结点
5、在m这一时刻,c1和c2都处于环入口结点,解决!!
3、实现代码
import java.util.*;
/*
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
*/
public class Solution {
public ListNode EntryNodeOfLoop(ListNode pHead) {
//将链表的情况分为:单个节点和非单个节点
//1、单个节点
if(pHead == pHead.next){ //单个存在环
return pHead;
}
if(pHead.next == null && pHead != pHead.next){ // 单个无环
return null;
}
/*
2、多个节点
思路为:在用双指针两者相遇的地方,使得其中一个为初始节点,另外一个
不变,两者每次走一步,再次相遇的地方就是入口
*/
ListNode cur1 = pHead, cur2 = pHead;
while(cur2 != null){
cur1 = cur1.next;
if(cur2.next == null || cur2.next.next == null){ //无环
return null;
}
cur2 = cur2.next.next;
//找到相遇的地方
if(cur1 == cur2){
cur1 = pHead;
break;
}
}
//从相遇的地方开始,两者一起出发,步长保持一致,再次相遇的地方就是入口
while(cur1 != cur2){
cur1 = cur1.next;
cur2 = cur2.next;
}
ListNode entrance = new ListNode(0);
entrance.val = cur1.val;
return entrance;
}
}
4、文末总结
通过这题,能很清楚的明白,写题目不仅要写得出来,还要讲得明白。⛽️
day8-9.16
1、问题描述
2、求解思路
该题的思路与返回倒数第k个节点有异曲同工之妙,其原理都是双指针,先让指针2向前移动n步,然后再让指针1和指针2同时移动,知道指针2为null为止,需要注意的是:返回的是整个链表,我们需要删除掉倒数第n个节点,为了让删除操作统一,我们设置一个虚拟头节点,并且创建一个节点pre始终保持在指针1的前一个节点,这样能够保证指针1指向倒数第n个节点的时候,可以顺利的删除!
3、实现代码
import java.util.*;
/*
* public class ListNode {
* int val;
* ListNode next = null;
* }
*/
public class Solution {
/**
*
* @param head ListNode类
* @param n int整型
* @return ListNode类
*/
public ListNode removeNthFromEnd (ListNode head, int n) {
// write code here
//1、首先判断是否是要删除头节点,所以采用虚拟头节点来解决
ListNode zero = new ListNode(-1);
zero.next = head;
//2、设置指针,遍历链表
ListNode pre = zero, cur1 = zero, cur2 = zero;
//3、先让cur2走n步
for(int i = 0; i < n; i++){
cur2 = cur2.next;
}
//4、同时让cur1和cur2一起走,知道cur2为null
while(cur2 != null){
pre = cur1;
cur1 = cur1.next;
cur2 = cur2.next;
}
//5、删除倒数第n个节点
pre.next = cur1.next;
return zero.next;
}
}
4、文末总结
这道题带来的收获是:1)编写代码的过程中注意边界情况;2)双指针在链表中的应用。
day8-9.16
1、问题描述
2、求解思路
2.1、method-one
- 求出链表1和链表2的长度length1和length2
- 求二者长度的差,temp
- 让比较长的链表走temp步
- 两个链表同时出发,直至二者指针相遇,相遇的地方即为相遇点
2.2、method-two
- 很巧妙的思路:二者指针同时出发
- 若有其中一个指针走到末尾,则令其从另外一个链表的头节点开始继续走
- 由于路程走的路程是一样的,那么他们一定会在公共点相遇
1、第三步可以这样理解,由上图以及题意可以看出,两个链表的非公共部分:[1,2,3],[4,5];公共部分:[6,7]
2、当二者肯定都会到底7(终点),此时指针1非公共部分走了3,指针2非公共部分走了2;
3、让他们交换初始位置,到达相遇的地方时,指针1走了2步,指针2走了3步;
4、算一下:指针1走了非公共部分3+2=5,以及公共部分2
指针2走了非公共部分2+3=5,以及公共部分2
5、意味着一起出发,路过终点后,第一次相遇的地方,就是二者的公共节点
3、实现代码
import java.util.*;
/*
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}*/
public class Solution {
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2)
{
if(pHead1 == null || pHead2 == null){
return null;
}
//1、求出链表pHead1和PHead2点长度
ListNode l1 = pHead1, l2 = pHead2, p1 = null, p2 = null;
int length1 = 0, length2 = 0;
while(l1 != null){
p1 = l1;
length1++;
l1 = l1.next;
}
while(l2 != null){
p2 = l2;
length2++;
l2 = l2.next;
}
//2、如果存在p1 != p2则返回null,没有共同节点
if(p1.val != p2.val){
return null;
}
// 重新初始化l1 和 l2
l1 = pHead1;
l2 = pHead2;
//3、否则求出两者之差,让长的先走temp步,两者再一起出发,直到相等
int temp = 0;
if(length1 >= length2){
temp = length1 - length2;
for(int i = 0; i < temp; i++){
l1 = l1.next;
}
}else{
temp = length2 - length1;
for(int i = 0; i < temp; i++){
l2 = l2.next;
}
}
//4、遍历l1he和l2,二者相等则返回
while(l1.val != l2.val){
l1 = l1.next;
l2 = l2.next;
}
return l1;
}
}
4、文末总结
写完题目的时候,虽然能ac,也多看看别人的想法!!
day8-9.15
1、问题描述
2、求解思路
2.1、methon-one(正向)
- 首先、将两个链表的值都存入栈中
- 其次、按顺序出栈,使用temp存非空栈出栈的值以及val1进位符之和
- 将temp%10作为节点的值,以头插法进行插入
- 返回虚拟头节点的下一个节点zero.next
2.2、methon-two(逆向)
- 反转两个链表
- 对两个链表逐个求和,并设置进位符,以方法一的思路
- 再次反转新链表
- 返回新链表头节点即可
3、实现代码(method-one)
import java.util.*;
/*
* public class ListNode {
* int val;
* ListNode next = null;
* }
*/
public class Solution {
/**
*
* @param head1 ListNode类
* @param head2 ListNode类
* @return ListNode类
*/
public ListNode addInList (ListNode head1, ListNode head2) {
// write code here
//1、使用栈来存储数值
Stack<Integer> s1 = new Stack<Integer>();
Stack<Integer> s2 = new Stack<Integer>();
ListNode l1 = head1, l2 = head2;
while(l1 != null){
s1.push(l1.val);
l1 = l1.next;
}
while(l2 != null){
s2.push(l2.val);
l2 = l2.next;
}
//2、不断的出栈,插入到新的链表中
// val1为当前两者计算的值取余,val2为两者和的商
int val1 = 0;
int temp = 0;
ListNode zero = new ListNode(-1);
while(!s1.isEmpty() || !s2.isEmpty() || val1 != 0){
if(!s2.isEmpty() && !s1.isEmpty()){
temp = s1.pop() + s2.pop() + val1;
}else if(!s1.isEmpty() && s2.isEmpty()){
temp = s1.pop() + val1;
}else{
temp = s2.pop() + val1;
}
// 插入操作
ListNode value = new ListNode(0);
value.val = temp % 10;
value.next = zero.next;
zero.next = value;
val1 = temp / 10;
}
return zero.next;
}
}
4、文末总结
争取更小的时空复杂度!!