【数据结构】二叉树经典基础习题
目录
单值二叉树
思路
代码
相同的树
思路
代码
二叉树的前序遍历
思路
代码
对称二叉树
思路
代码
另一棵树的子树
思路
代码
二叉树遍历(较难)
思路
代码
平衡二叉树
思路
代码
单值二叉树
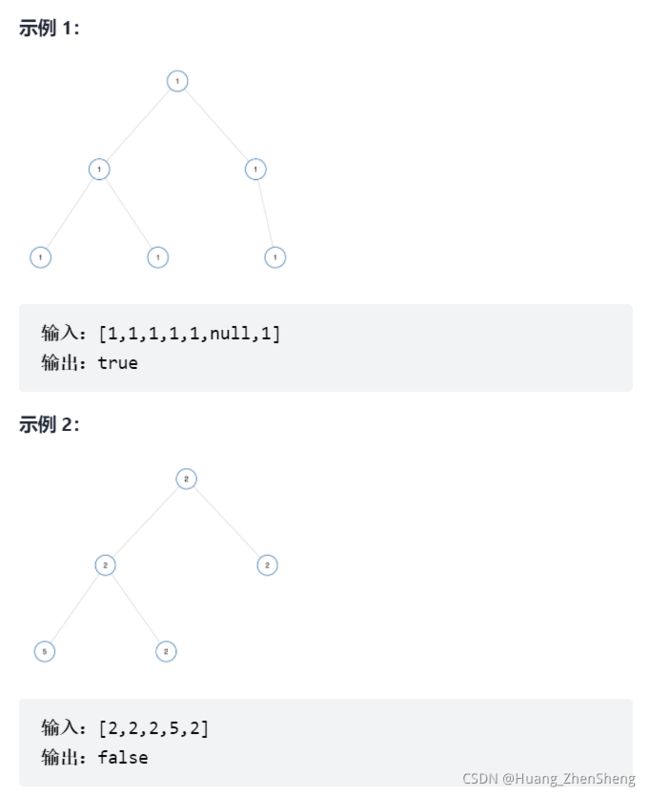
OJ:如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false
思路
代码
bool isUnivalTree(struct TreeNode* root)
{
if(root == NULL)
return true;
if(root->left && root->left->val != root->val)//跟左孩子比
return false;
if(root->right && root->right->val != root->val)//跟右孩子比
return false;
return isUnivalTree(root->left) && isUnivalTree(root->right);
}相同的树
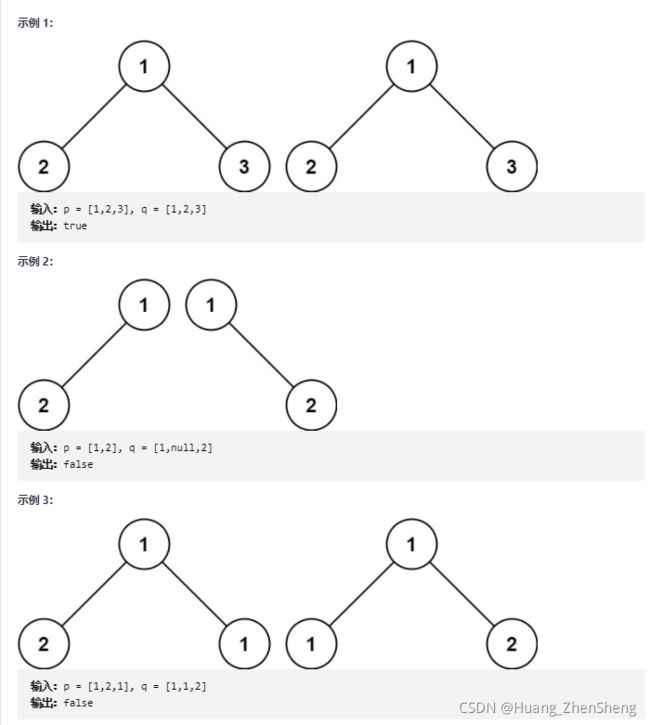
OJ给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
思路
当前根节点和子树,分治思想
直接拿结果的情况:
第一种:p和q都为空
第二种:p为空,q不为空,或者p不为空,q为空
第三种:二者都不为空,p和q的值不相等
代码
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p == NULL && q==NULL)
return true;
if(p == NULL || q==NULL)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left)&& isSameTree(p->right,q->right);
}时间复杂度:看递归次数,每个节点都要比常数次,这颗树有N个节点,递归N次,O(N)
空间复杂度:空间可以重复利用,最坏:O(h)= O(N)
二叉树的前序遍历
OJ给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
思路
第一个问题:开多大的数组?——写一个子函数将这颗树的大小算出来
第二个问题:写一个子函数递归,把值往数组里面放!注意这里i得传址
代码
int preorderSize(struct TreeNode*proot)//二叉树的大小
{
if(proot == NULL)
return NULL;
else
return 1+preorderSize(proot->left)+preorderSize(proot->right);
}
void _preorderTraversal(struct TreeNode*root,int*arr,int*i)
{
if(root == NULL)
return;
arr[(*i)++] = root->val;//根
_preorderTraversal(root->left,arr,i);//左子树
_preorderTraversal(root->right,arr,i);//右子树
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
*returnSize = preorderSize(root);
int*arr = malloc(sizeof(arr)* (*returnSize));
int i = 0;
_preorderTraversal(root,arr,&i);
return arr;
}对称二叉树
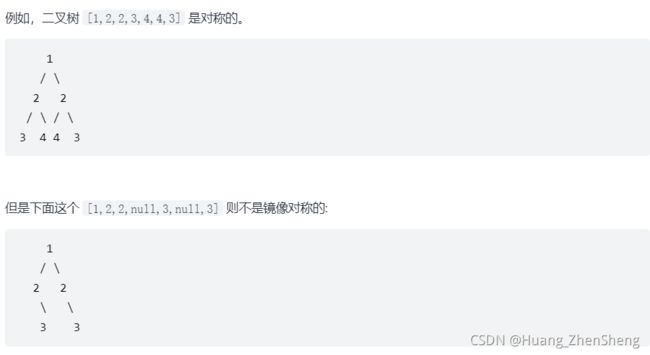
OJ给定一个二叉树,检查它是否是镜像对称的。
思路
左右比较,所以在这里加一个子函数
左子树的左孩子VS右子树的右孩子
左子树的右孩子VS右子树的左孩子
代码
bool _isSymmetric(struct TreeNode* pleft,struct TreeNode* pright)
{
if(pleft == NULL && pright == NULL)
return true;
if(pleft == NULL || pright == NULL)
return false;
if(pleft->val != pright->val)
return false;
return _isSymmetric(pleft->left,pright->right) && _isSymmetric(pleft->right,pright->left);
}
bool isSymmetric(struct TreeNode* root)
{
if(root == NULL)
return true;
return _isSymmetric(root->left,root->right);
}另一棵树的子树
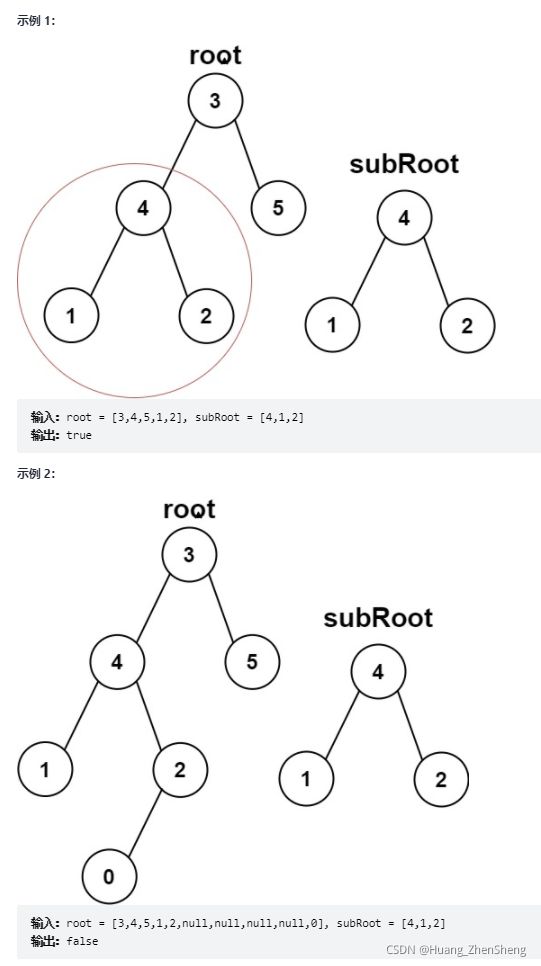
OJ给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
思路
遍历一下root,拿到每个子树的根,跟subRoot这颗树比较
调用两树相同的代码
代码
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if(p == NULL && q==NULL)
return true;
if(p == NULL || q==NULL)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left)&& isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
if(root == NULL)
return false;
if(isSameTree(root,subRoot))
return true;
return isSubtree(root->left,subRoot)
|| isSubtree(root->right,subRoot);
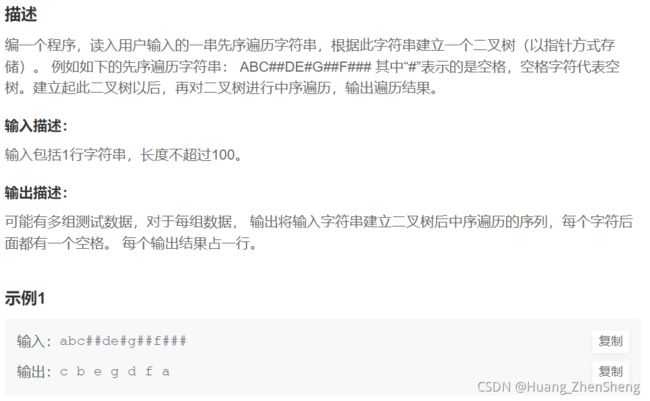
}二叉树遍历(较难)
IO
思路
先构建出这个二叉树,然后在进行中序遍历
代码
#include
#include
struct TreeNode
{
char val;
struct TreeNode*left;
struct TreeNode*right;
};
//构建这颗二叉树
struct TreeNode* CreateTree(char*str, int*i)
{
if (str[(*i)] == '#')
{
(*i)++;
return NULL;
}
struct TreeNode*root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
root->val = str[(*i)++];
root->left = CreateTree(str, i);
root->right = CreateTree(str, i);
return root;
}
//中序遍历
void InOrder(struct TreeNode* root)
{
if (root == NULL)
return;
InOrder(root->left);
printf("%c ", root->val);
InOrder(root->right);
}
int main()
{
char str[100];
scanf("%s", str);
int i = 0;
struct TreeNode* root = CreateTree(str, &i);//构建这颗二叉树
InOrder(root);//中序遍历
return 0;
} 平衡二叉树
OJ给定一个二叉树,判断它是否是高度平衡的二叉树。
一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
思路
1,树若为空,则返回true
2,求root左子树的高度和root右子树的高度
3,检测root左右子树是否满足平衡二叉树的定义----->高度差的绝对值
4,递归root左子树&&root右子树
代码
int BinaryTreeDepth(struct TreeNode*root)
{
if(root == NULL)
return 0;
int leftleaf = BinaryTreeDepth(root->left);
int rightleaf = BinaryTreeDepth(root->right);
return leftleaf > rightleaf ? leftleaf+1:rightleaf+1;
}
bool isBalanced(struct TreeNode* root)
{
if(root == NULL)
return true;
if(abs( BinaryTreeDepth(root->left) - BinaryTreeDepth(root->right) )>1)
return false;
return isBalanced(root->left) && isBalanced(root->right);
}