折半查找包含程序

折半查找又称二分查找，它仅适用于有序的顺序表

以下面的例子来讲解折半查找的过程

元素	7	10	13	16	19	29	32	33	37	41	43
数组位置	0	1	2	3	4	5	6	7	8	9	10

 第一步：先确定查找元素，以14为例子；low和high分别是指向表的上界和下界；最开是low指向0，high指向10，mid = (low+high)/2 = 5规定向下取整（程序实现的时候计算机规定的是向下取整）

元素	7	10	13	16	19	29	32	33	37	41	43
数组位置	0	1	2	3	4	5	6	7	8	9	10
	low					mid					high

第二步：通过mid位置元素的值，和想要查找元素进行比较；29>14,由于是顺序表，可以知道14肯定是在29左边，因为high规定是指向表的下界，因为mid之前已经比较过了，所以high肯定是指向mid前面一个元素的位置；此时high = 4;low = 0不变；  mid = (low+high)/2 = 2;

元素	7	10	13	16	19	29	32	33	37	41	43
数组位置	0	1	2	3	4	5	6	7	8	9	10
	low		mid		high

第三步：重复第二部的工作，通过mid位置元素的值，和想要查找元素进行比较；13<14,由于是顺序表，所以肯定知道14在13的右边，因为low指向的是表的上界，所以此时low = mid+1 = 3;high = 4不变；mid = (low+high)/2 = 3.5向下取整为3

元素	7	10	13	16	19	29	32	33	37	41	43
数组位置	0	1	2	3	4	5	6	7	8	9	10
				low mid	high

第四步：因为16>14,所以high = mid-1 = 2,此时low>high表示查找失败，没有该元素

元素	7	10	13	16	19	29	32	33	37	41	43
数组位置	0	1	2	3	4	5	6	7	8	9	10
			high	low

//折半查找
int Binary_Search(SSTable L, int key)
{
	int low = 0, high = L.length-1, mid;//low表示查找表第一个元素的位置，high表示查找表最后一个元素的位置，mid表示中间元素的位置
	while(low <= high)
	{
	  mid = (low+high)/2;//取中间位置，向下取整
	  if(L.elem[mid] == key)
		  return mid;//若查找成功则返回所在位置
	  else if(L.elem[mid] > key)
	  {
	    high = mid-1;//从前半部分查找
	  }
	  else
	  {
	    low = mid+1;//从后半部分继续查找
	  }

	}
	return -1;//查找失败返回-1
}

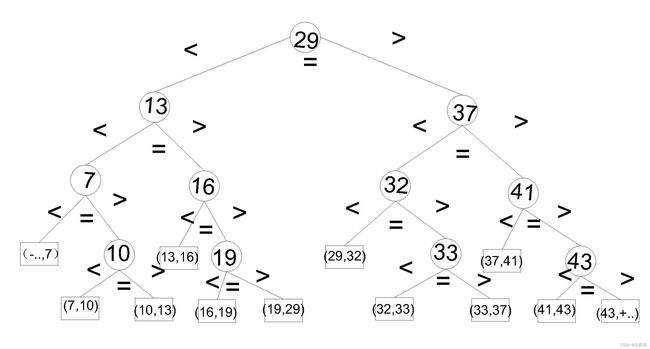
折半查找的过程可以用二叉树来描述，称为判定树

树中的叶节点都是方块的形状，它表示的是查找不成功；圆圈表示非终端结点，表示查找表中的元素；若非终端元素为n个,则方块的则有n+1个 = 成功结点的空链域数量；判定树是一棵平衡二叉树

h是树高，并且元素个数是n时树高向上取整,所以时间复杂度为O() ,平均情况下比顺序查找的效率高，但是不是折半查找一定比顺序查找效率高

mid向下取整时：

如果当前low和high之间有奇数个元素，则mid分隔后，左右两部分元素个数相等

如果当前low和high之间有偶数个元素，则mid分隔后，左半部分比右半部分少一个元素

总结：右子树结点数  -  左子树结点数 = 0或1

程序：

1.数组结构体

//定义动态数组结构体
typedef struct
{//查找表得数据结构--顺序表
  int *elem;//动态数组的基址
  int length;//表的长度
}SSTable;

 2.创造数组

void CreatSSTable(SSTable &L)
{
  int len;
  printf("请输入你想查找表的长度为：\n");
  scanf_s("%d",&len);
  L.length = len;
  L.elem = (int *)malloc(sizeof(int)*L.length);
  int val;//用于暂存查找表的元素
  for(int i = 0; i < L.length; ++i)
  {
	  printf("请输入第%d个元素：",i+1);
	  scanf_s("%d",&val);
	  L.elem[i] = val;
  }
}

3.折半查找

//折半查找
int Binary_Search(SSTable L, int key)
{
	int low = 0, high = L.length-1, mid;//low表示查找表第一个元素的位置，high表示查找表最后一个元素的位置，mid表示中间元素的位置
	while(low <= high)
	{
	  mid = (low+high)/2;//向下取整
	  if(L.elem[mid] == key)
		  return mid;
	  else if(L.elem[mid] > key)
	  {
	    high = mid-1;
	  }
	  else
	  {
	    low = mid+1;
	  }

	}
	return -1;//查找失败返回-1
}

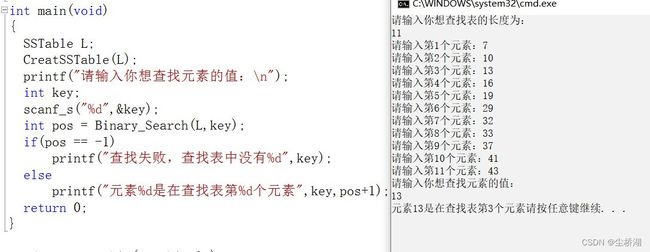
4.运行结果

完整程序

#include
#include
#include

//定义动态数组结构体
typedef struct
{//查找表得数据结构--顺序表
  int *elem;//动态数组的基址
  int length;//表的长度
}SSTable;

//函数说明
void CreatSSTable(SSTable &L);
int Binary_Search(SSTable L, int key);

int main(void)
{
  SSTable L;
  CreatSSTable(L);
  printf("请输入你想查找元素的值：\n");
  int key;
  scanf_s("%d",&key);
  int pos = Binary_Search(L,key);
  if(pos == -1)
	  printf("查找失败，查找表中没有%d",key);
  else
	  printf("元素%d是在查找表第%d个元素",key,pos+1);
  return 0;
}

void CreatSSTable(SSTable &L)
{
  int len;
  printf("请输入你想查找表的长度为：\n");
  scanf_s("%d",&len);
  L.length = len;
  L.elem = (int *)malloc(sizeof(int)*L.length);
  int val;//用于暂存查找表的元素
  for(int i = 0; i < L.length; ++i)
  {
	  printf("请输入第%d个元素：",i+1);
	  scanf_s("%d",&val);
	  L.elem[i] = val;
  }
}

//折半查找
int Binary_Search(SSTable L, int key)
{
	int low = 0, high = L.length-1, mid;//low表示查找表第一个元素的位置，high表示查找表最后一个元素的位置，mid表示中间元素的位置
	while(low <= high)
	{
	  mid = (low+high)/2;//向下取整
	  if(L.elem[mid] == key)
		  return mid;
	  else if(L.elem[mid] > key)
	  {
	    high = mid-1;
	  }
	  else
	  {
	    low = mid+1;
	  }

	}
	return -1;//查找失败返回-1
}