高数之不定积分
文章目录
- 一、第一类换元法
-
- 1.核心公式
- 2.基本积分
-
- (1)分式
- (2)三角函数
- 3.写法
-
- (1)凑微分法
- (2)常见凑微分形式:
- 4.题
-
- (1)第一类换元法的基本应用
- (2)第一类换元法和分式加减分解
- (3)三角函数专题
- 二、第二类换元法
-
- 1.核心公式
- 2.常用三种变量代换
-
- (1)知识点
- (2)题
- 3.出错点
- 4.题
-
- (1)第二类换元法的基本应用
- (2)难题
- 三、分部积分法
-
- 1.公式
- 2.解析
一、第一类换元法
1.核心公式
∫ f [ ϕ ( x ) ] ϕ ′ ( x ) d x = ∫ f ( u ) d u ∣ u = ϕ ( x ) = F ( u ) + C \int f[\phi(x)]\phi'(x)dx=\int f(u)du|_{u=\phi(x)}=F(u)+C ∫f[ϕ(x)]ϕ′(x)dx=∫f(u)du∣u=ϕ(x)=F(u)+C
【思路】:
合并,从整体的角度将其化成基本积分解决。
【用法】:
找到可以化为基本积分形式的 f ( u ) f(u) f(u),然后变换积分部分构造成满足 d u du du的样子。
比如: ∫ 4 x e x 2 d x \displaystyle \int 4xe^{x^2}dx ∫4xex2dx, e x 2 e^{x^2} ex2就是 f ( u ) f(u) f(u),那么其他部分变换成 d u du du的样子, d u = d ( x 2 ) = 2 x d x du=d(x^2)=2xdx du=d(x2)=2xdx,所以 ∫ 4 x e x 2 d x = ∫ 2 e x 2 d ( x 2 ) = 2 e x 2 + C \displaystyle \int 4xe^{x^2}dx=\displaystyle \int 2e^{x^2}d(x^2)=2e^{x^2}+C ∫4xex2dx=∫2ex2d(x2)=2ex2+C
2.基本积分
完整版:
https://wenku.baidu.com/view/8eeeeb6c561252d380eb6e08.html
https://blog.csdn.net/yellow_hill/article/details/82977844
(1)分式
【最基本的ln】
- ∫ 1 x d x = l n ∣ x ∣ + C \displaystyle \int \dfrac{1}{x}dx= ln|x|+C ∫x1dx=ln∣x∣+C
记着绝对值
x x x要是负的还得对 − x -x −x求导得到 − 1 -1 −1,如 ∫ 1 a − x d x = − ln ( a − x ) d x \displaystyle \int \dfrac{1}{a-x}dx=-\ln{(a-x)} dx ∫a−x1dx=−ln(a−x)dx
【反三角函数】
-
∫ 1 1 − x 2 d x = arcsin x + C \displaystyle \int \dfrac{1}{\sqrt{1-x^2}}dx=\arcsin{x}+C ∫1−x21dx=arcsinx+C
∫ 1 a 2 − x 2 d x = arcsin x a + C ( a = ̸ 0 ) \displaystyle \int \dfrac{1}{\sqrt{a^2-x^2}}dx=\arcsin{\frac{x}{a}}+C \quad (a=\not 0) ∫a2−x21dx=arcsinax+C(a≠0) -
∫ 1 1 + x 2 d x = arctan x + C \displaystyle \int \dfrac{1}{1+x^2}dx=\arctan{x}+C ∫1+x21dx=arctanx+C
∫ 1 a 2 + x 2 d x = 1 a arctan x a + C ( a = ̸ 0 ) \displaystyle \int \dfrac{1}{a^2+x^2}dx=\frac{1}{a}\arctan{\frac{x}{a}}+C \quad (a=\not 0) ∫a2+x21dx=a1arctanax+C(a≠0)
【 x 2 ± a 2 x^2 \pm a^2 x2±a2】
-
∫ 1 x 2 − a 2 d x = ∫ 1 x − a 1 x + a d x = ∫ 1 2 a ( 1 x − a − 1 x + a ) d x = 1 2 a ( ln ∣ x − a ∣ − ln ∣ x + a ∣ ) + C = 1 2 a ln ∣ x − a x + a ∣ + C \displaystyle \int \dfrac{1}{x^2-a^2}dx=\displaystyle \int \dfrac{1}{x-a} \dfrac{1}{x+a} dx=\displaystyle \int \dfrac{1}{2a} (\dfrac{1}{x-a} -\dfrac{1}{x+a})dx=\dfrac{1}{2a}(\ln|x-a|-\ln|x+a|)+C=\dfrac{1}{2a}\ln|{\dfrac{x-a}{x+a}}|+C ∫x2−a21dx=∫x−a1x+a1dx=∫2a1(x−a1−x+a1)dx=2a1(ln∣x−a∣−ln∣x+a∣)+C=2a1ln∣x+ax−a∣+C
-
∫ 1 a 2 − x 2 d x = − ∫ 1 x 2 − a 2 d x = ∫ 1 2 a ( − 1 x − a + 1 x + a ) d x = 1 2 a ( − ln ∣ x − a ∣ + ln ∣ x + a ∣ ) + C = 1 2 a ln ∣ x + a x − a ∣ + C \displaystyle \int \dfrac{1}{a^2-x^2}dx =-\displaystyle \int \dfrac{1}{x^2-a^2}dx =\displaystyle \int \dfrac{1}{2a} (-\dfrac{1}{x-a} +\dfrac{1}{x+a})dx =\dfrac{1}{2a}(-\ln|x-a|+\ln|x+a|)+C =\dfrac{1}{2a}\ln|{\dfrac{x+a}{x-a}}|+C ∫a2−x21dx=−∫x2−a21dx=∫2a1(−x−a1+x+a1)dx=2a1(−ln∣x−a∣+ln∣x+a∣)+C=2a1ln∣x−ax+a∣+C
有请智商下线的沙雕推演:
- ∫ 1 a 2 − x 2 d x = ∫ 1 a − x 1 a + x d x = ∫ 1 2 a ( 1 a − x + 1 a + x ) d x = ̸ 1 2 a ( ln ∣ a − x ∣ + ln ∣ a + x ∣ ) + C = 1 2 a ln ( ∣ a − x ∣ ∣ a + x ∣ ) + C \displaystyle \int \dfrac{1}{a^2-x^2}dx =\displaystyle \int \dfrac{1}{a-x} \dfrac{1}{a+x} dx =\displaystyle \int \dfrac{1}{2a} (\dfrac{1}{a-x} +\dfrac{1}{a+x})dx =\not \dfrac{1}{2a}(\ln|a-x|+\ln|a+x|)+C =\dfrac{1}{2a}\ln(|a-x||a+x|)+C ∫a2−x21dx=∫a−x1a+x1dx=∫2a1(a−x1+a+x1)dx≠2a1(ln∣a−x∣+ln∣a+x∣)+C=2a1ln(∣a−x∣∣a+x∣)+C
注意:
∫ 1 a − x d x = − ln ( a − x ) d x \displaystyle \int \dfrac{1}{a-x}dx=-\ln{(a-x)} dx ∫a−x1dx=−ln(a−x)dx,不是 = ln ( a − x ) d x =\ln{(a-x)}dx =ln(a−x)dx
所以正确是
∫ 1 a 2 − x 2 d x = 1 2 a ( − ln ∣ a − x ∣ + ln ∣ a + x ∣ ) + C = 1 2 a ln ∣ x + a x − a ∣ + C \displaystyle \int \dfrac{1}{a^2-x^2}dx =\dfrac{1}{2a}(-\ln|a-x|+\ln|a+x|)+C =\dfrac{1}{2a}\ln|{\dfrac{x+a}{x-a}}|+C ∫a2−x21dx=2a1(−ln∣a−x∣+ln∣a+x∣)+C=2a1ln∣x−ax+a∣+C
【 x 2 ± a 2 \sqrt{x^2 \pm a^2} x2±a2】
-
∫ 1 x 2 + a 2 d x = ln ( x + x 2 + a 2 ) + C \displaystyle \int \dfrac{1}{\sqrt{x^2+a^2}}dx=\ln(x+\sqrt{x^2+a^2})+C ∫x2+a21dx=ln(x+x2+a2)+C
-
∫ 1 x 2 − a 2 d x = ln ( x + x 2 − a 2 ) + C \displaystyle \int \dfrac{1}{\sqrt{x^2-a^2}}dx=\ln(x+\sqrt{x^2-a^2})+C ∫x2−a21dx=ln(x+x2−a2)+C
(2)三角函数
-
∫ 1 sin 2 x d x = ∫ csc 2 x d x = − cot x + C \displaystyle \int \dfrac{1}{\sin^2{x}}dx=\displaystyle \int \csc^2{x}dx=-\cot{x}+C ∫sin2x1dx=∫csc2xdx=−cotx+C
-
∫ 1 cos 2 x d x = ∫ sec 2 x d x = tan x + C \displaystyle \int \dfrac{1}{\cos^2{x}}dx=\displaystyle \int \sec^2{x}dx=\tan{x}+C ∫cos2x1dx=∫sec2xdx=tanx+C
-
∫ sec x d x = ln ∣ sec x + tan x ∣ + C \displaystyle \int \sec{x}dx=\ln|\sec{x}+\tan{x}|+C ∫secxdx=ln∣secx+tanx∣+C
-
∫ sec 2 x d x = tan x + C \displaystyle \int \sec^2{x}dx=\tan{x}+C ∫sec2xdx=tanx+C
-
∫ csc x = ln ∣ csc x − cot x ∣ + C = ln ∣ tan x x ∣ + C \displaystyle \int \csc{x}=\ln|\csc{x}-\cot{x}|+C=\ln|\tan{\frac{x}{x}}|+C ∫cscx=ln∣cscx−cotx∣+C=ln∣tanxx∣+C
-
∫ csc 2 x = − cot x + C \displaystyle \int \csc^2{x}=-\cot{x}+C ∫csc2x=−cotx+C
-
∫ tan x = − ln ∣ cos x ∣ + C \displaystyle \int \tan{x}=-\ln|\cos{x}|+C ∫tanx=−ln∣cosx∣+C
-
∫ cot x = ln ∣ sin x ∣ + C \displaystyle \int \cot{x}=\ln|\sin{x}|+C ∫cotx=ln∣sinx∣+C
-
∫ sec x tan x d x = sec x + C \displaystyle \int \sec{x} \tan{x}dx=\sec{x}+C ∫secxtanxdx=secx+C
-
∫ csc x cot x d x = − csc x + C \displaystyle \int \csc{x} \cot{x}dx=-\csc{x}+C ∫cscxcotxdx=−cscx+C
3.写法
(1)凑微分法
用第一类换元法,那么我们就要想法设法凑成 d ( ϕ ( x ) ) d(\phi(x)) d(ϕ(x))以便代入基本积分,所以叫凑微分法。
如: ∫ 2 x e x 2 d x = ∫ e x 2 d ( x 2 ) = e x 2 + C \displaystyle \int 2xe^{x^2}dx=\displaystyle \int e^{x^2}d(x^2)=e^{x^2}+C ∫2xex2dx=∫ex2d(x2)=ex2+C
(2)常见凑微分形式:
-
∫ f ( a x + b ) d x = 1 a ∫ f ( a x + b ) d ( a x + b ) \displaystyle \int f(ax+b)dx =\dfrac{1}{a} \displaystyle \int f(ax+b)d(ax+b) ∫f(ax+b)dx=a1∫f(ax+b)d(ax+b)
-
∫ x m f ( a x m + 1 + b ) d x = 1 a ( m + 1 ) ∫ f ( a x m + 1 + b ) d ( a x m + 1 + b ) ( m = ̸ − 1 ) \displaystyle \int x^mf(ax^{m+1}+b)dx =\dfrac{1}{a(m+1)} \displaystyle \int f(ax^{m+1}+b)d(ax^{m+1}+b) \quad (m=\not -1) ∫xmf(axm+1+b)dx=a(m+1)1∫f(axm+1+b)d(axm+1+b)(m≠−1)
-
∫ f ( x ) 1 x d x = 2 ∫ f ( x ) d ( x ) \displaystyle \int f(\sqrt{x})\dfrac{1}{\sqrt{x}}dx =2\displaystyle \int f(\sqrt{x})d(\sqrt{x}) ∫f(x)x1dx=2∫f(x)d(x)
-
∫ f ( e x ) e x d x = ∫ f ( e x ) d ( e x ) \displaystyle \int f(e^x)e^xdx =\displaystyle \int f(e^x)d(e^x) ∫f(ex)exdx=∫f(ex)d(ex)
-
∫ f ( ln x ) 1 x d x = ∫ f ( ln x ) d ( ln x ) \displaystyle \int f(\ln{x})\dfrac{1}{x}dx =\displaystyle \int f(\ln{x})d(\ln{x}) ∫f(lnx)x1dx=∫f(lnx)d(lnx)
-
∫ f ( sin x ) cos x d x = ∫ f ( sin x ) d ( sin x ) \displaystyle \int f(\sin{x})\cos{x}dx =\displaystyle \int f(\sin{x})d(\sin{x}) ∫f(sinx)cosxdx=∫f(sinx)d(sinx)
-
∫ f ( cos x ) sin x d x = − ∫ f ( cos x ) d ( cos x ) \displaystyle \int f(\cos{x})\sin{x}dx =-\displaystyle \int f(\cos{x})d(\cos{x}) ∫f(cosx)sinxdx=−∫f(cosx)d(cosx)
-
∫ f ( tan x ) 1 cos 2 x d x = ∫ f ( tan x ) d ( tan x ) \displaystyle \int f(\tan{x})\dfrac{1}{\cos^2{x}}dx =\displaystyle \int f(\tan{x})d(\tan{x}) ∫f(tanx)cos2x1dx=∫f(tanx)d(tanx)
-
∫ f ( arcsin x ) 1 1 − x 2 = ∫ f ( arcsin x ) d ( arcsin x ) \displaystyle \int f(\arcsin{x})\dfrac{1}{\sqrt{1-x^2}} =\displaystyle \int f(\arcsin{x})d(\arcsin{x}) ∫f(arcsinx)1−x21=∫f(arcsinx)d(arcsinx)
-
∫ f ( arctan x ) 1 1 + x 2 = ∫ f ( arctan x ) d ( arctan x ) \displaystyle \int f(\arctan{x})\dfrac{1}{\sqrt{1+x^2}} =\displaystyle \int f(\arctan{x})d(\arctan{x}) ∫f(arctanx)1+x21=∫f(arctanx)d(arctanx)
4.题
(1)第一类换元法的基本应用
-
∫ 2 c o s 2 x d x \displaystyle \int 2cos2xdx ∫2cos2xdx
= ∫ c o s 2 x ( 2 x ) ′ d x = ∫ c o s u d u ∣ u = 2 x = s i n 2 x + C =\displaystyle \int cos2x(2x)'dx=\displaystyle \int cosudu|_{u=2x}=sin2x+C =∫cos2x(2x)′dx=∫cosudu∣u=2x=sin2x+C -
∫ 2 x e x 2 d x \displaystyle \int 2xe^{x^2}dx ∫2xex2dx
= ∫ e x 2 d ( x 2 ) = e x 2 + C =\displaystyle \int e^{x^2}d(x^2)=e^{x^2}+C =∫ex2d(x2)=ex2+C -
∫ 1 3 + 2 x d x \displaystyle \int \dfrac{1}{3+2x}dx ∫3+2x1dx
= ∫ 1 2 1 3 + 2 x ( 3 + 2 x ) ′ d x = 1 2 ∫ 1 u d u ∣ u = 3 + 2 x = 1 2 ln ∣ 3 + 2 x ∣ + C =\displaystyle \int \dfrac{1}{2}\dfrac{1}{3+2x}(3+2x)'dx=\dfrac{1}{2} \displaystyle \int\dfrac{1}{u}du|_{u=3+2x}=\dfrac{1}{2}\ln|3+2x|+C =∫213+2x1(3+2x)′dx=21∫u1du∣u=3+2x=21ln∣3+2x∣+C -
∫ 1 x ( 1 + 2 ln x ) d x \displaystyle \int \dfrac{1}{x(1+2\ln{x})}dx ∫x(1+2lnx)1dx
= ∫ 1 2 1 1 + 2 ln x d ( 1 + 2 ln x ) = 1 2 ln ( 1 + 2 ln x ) + C =\displaystyle \int \dfrac{1}{2} \dfrac{1}{1+2\ln{x}}d(1+2\ln x)=\dfrac{1}{2}\ln{(1+2\ln{x})}+C =∫211+2lnx1d(1+2lnx)=21ln(1+2lnx)+C -
∫ x 1 − x 2 d x \displaystyle \int x \sqrt{1-x^2}dx ∫x1−x2dx
= ∫ − 1 2 1 − x 2 d ( 1 − x 2 ) = ∫ − 1 2 ( 1 − x 2 ) 1 2 d ( 1 − x 2 ) = − 1 2 2 3 ( 1 − x 2 ) 3 2 + C = − 1 3 ( 1 − x 2 ) 3 2 + C =\displaystyle \int -\frac{1}{2} \sqrt{1-x^2}d(1-x^2)=\displaystyle \int -\frac{1}{2} {(1-x^2)}^{\frac{1}{2}} d(1-x^2)=-\dfrac{1}{2}\dfrac{2}{3}(1-x^2)^{\frac{3}{2}}+C=-\dfrac{1}{3}(1-x^2)^{\frac{3}{2}}+C =∫−211−x2d(1−x2)=∫−21(1−x2)21d(1−x2)=−2132(1−x2)23+C=−31(1−x2)23+C
(2)第一类换元法和分式加减分解
- ∫ x 2 ( x + 2 ) 3 d x \displaystyle \int \dfrac{x^2}{(x+2)^3}dx ∫(x+2)3x2dx
= ∫ [ ( x + 2 ) − 2 ] 2 ( x + 2 ) 3 d x = ∫ ( u − 2 ) 2 u 3 d u ∣ u = x + 2 = ∫ ( 1 u − 4 u 2 + 4 u 3 ) d u = ln ∣ u ∣ + 4 u − 2 u 2 + C = ln ∣ x + 2 ∣ + 4 x + 2 − 2 ( x + 2 ) 2 + C =\displaystyle \int \dfrac{[(x+2)-2]^2}{(x+2)^3}dx=\displaystyle \int \dfrac{(u-2)^2}{u^3}du|_{u=x+2}=\displaystyle \int (\dfrac{1}{u} - \dfrac{4}{u^2}+\dfrac{4}{u^3})du=\ln|u|+\dfrac{4}{u}-\dfrac{2}{u^2}+C=\ln|x+2|+\dfrac{4}{x+2}-\dfrac{2}{(x+2)^2}+C =∫(x+2)3[(x+2)−2]2dx=∫u3(u−2)2du∣u=x+2=∫(u1−u24+u34)du=ln∣u∣+u4−u22+C=ln∣x+2∣+x+24−(x+2)22+C
(3)三角函数专题
-
∫ 1 9 − x 2 d x \displaystyle \int \dfrac{1}{\sqrt{9-x^2}}dx ∫9−x21dx
= ∫ 1 3 1 1 − ( x 3 ) 2 d x = ∫ 1 1 − ( x 3 ) 2 d ( x 3 ) = arcsin x 3 + C =\displaystyle \int \dfrac{1}{3} \dfrac{1}{\sqrt{1-(\frac{x}{3})^2}}dx=\displaystyle \int \dfrac{1}{\sqrt{1-(\frac{x}{3})^2}}d(\frac{x}{3})=\arcsin{\frac{x}{3}}+C =∫311−(3x)21dx=∫1−(3x)21d(3x)=arcsin3x+C -
∫ 1 9 + x 2 d x \displaystyle \int \dfrac{1}{9+x^2}dx ∫9+x21dx
= ∫ 1 9 1 1 + ( x 3 ) 2 d x = ∫ 1 3 1 1 + ( x 3 ) 2 d ( x 3 ) = 1 3 arctan x 3 + C =\displaystyle \int \dfrac{1}{9} \dfrac{1}{1+(\frac{x}{3})^2}dx=\displaystyle \int \dfrac{1}{3} \dfrac{1}{1+(\frac{x}{3})^2}d(\frac{x}{3})=\frac{1}{3}\arctan{\frac{x}{3}}+C =∫911+(3x)21dx=∫311+(3x)21d(3x)=31arctan3x+C
二、第二类换元法
1.核心公式
设, x = ϕ ( u ) x=\phi(u) x=ϕ(u),
∫ f ( x ) d x = ∫ f [ ϕ ( u ) ] ϕ ′ ( u ) ( x ) d u ∣ u = ϕ − 1 ( x ) \int f(x)dx=\int f[\phi(u)]\phi'(u)(x)du|_{u=\phi^{-1}(x)} ∫f(x)dx=∫f[ϕ(u)]ϕ′(u)(x)du∣u=ϕ−1(x)
【思路】:
,从整体的角度将其化成基本积分解决。
【用法】:
找到可以化为基本积分形式的 f ( u ) f(u) f(u),然后变换积分部分构造成满足 d u du du的样子。
比如: ∫ 4 x e x 2 d x \displaystyle \int 4xe^{x^2}dx ∫4xex2dx, e x 2 e^{x^2} ex2就是 f ( u ) f(u) f(u),那么其他部分变换成 d u du du的样子, d u = d ( x 2 ) = 2 x d x du=d(x^2)=2xdx du=d(x2)=2xdx,所以 ∫ 4 x e x 2 d x = ∫ 2 e x 2 d ( x 2 ) = 2 e x 2 + C \displaystyle \int 4xe^{x^2}dx=\displaystyle \int 2e^{x^2}d(x^2)=2e^{x^2}+C ∫4xex2dx=∫2ex2d(x2)=2ex2+C
2.常用三种变量代换
(1)知识点
-
被积函数含有 a 2 − x 2 \sqrt{a^2-x^2} a2−x2,令 x = a sin t ( 或 cos t ) x=a\sin{t} \quad (或\cos{t}) x=asint(或cost), t ∈ ( − π / 2 , π / 2 ) t \in (-\pi/2,\pi/2) t∈(−π/2,π/2)
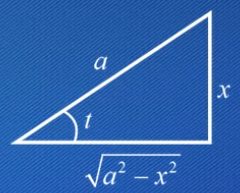
sin t = x a \sin{t}=\dfrac{x}{a} sint=ax,则第三边为 a 2 − x 2 \sqrt{a^2-x^2} a2−x2 -
被积函数含有 x 2 − a 2 \sqrt{x^2-a^2} x2−a2,令 x = a sec t x=a\sec{t} x=asect, t ∈ ( − π / 2 , π / 2 ) t \in (-\pi/2,\pi/2) t∈(−π/2,π/2)

sec t = x a \sec{t}=\dfrac{x}{a} sect=ax,则第三边为 x 2 − a 2 \sqrt{x^2-a^2} x2−a2 -
被积函数含有 a 2 + x 2 \sqrt{a^2+x^2} a2+x2,令 x = a tan t x=a\tan{t} x=atant, t ∈ ( − π / 2 , π / 2 ) t \in (-\pi/2,\pi/2) t∈(−π/2,π/2)

tan t = x a \tan{t}=\dfrac{x}{a} tant=ax,则第三边为 a 2 + x 2 \sqrt{a^2+x^2} a2+x2
(2)题
-
【代换1】
∫ a 2 − x 2 d x ( a > 0 ) \displaystyle \int \sqrt{a^2-x^2}dx \quad (a>0) ∫a2−x2dx(a>0)
令 x = a sin t x=a\sin{t} x=asint, t ∈ ( − π / 2 , π / 2 ) t \in (-\pi/2,\pi/2) t∈(−π/2,π/2),则
∫ a 2 − x 2 d x = ∫ a 2 ( 1 − sin 2 t ) d x = ∫ a cos t d x = ∫ a cos t a cos t d t = a 2 ∫ 1 + cos 2 t 2 d t = a 2 2 ( t + 1 2 sin 2 t ) + C = a 2 2 ( t + sin t cos t ) + C \displaystyle \int \sqrt{a^2-x^2}dx =\displaystyle \int \sqrt{a^2{(1-\sin^2{t})}}dx =\displaystyle \int a\cos{t}dx =\displaystyle \int a\cos{t} a\cos{t}dt =a^2 \displaystyle \int \dfrac{1+\cos{2t}}{2}dt =\dfrac{a^2}{2}(t+\dfrac{1}{2}\sin{2t})+C =\dfrac{a^2}{2}(t+\sin{t}\cos{t})+C ∫a2−x2dx=∫a2(1−sin2t)dx=∫acostdx=∫acostacostdt=a2∫21+cos2tdt=2a2(t+21sin2t)+C=2a2(t+sintcost)+C
由 sin t = x a \sin{t}=\dfrac{x}{a} sint=ax,得 cos t = a 2 − x 2 a \cos{t}=\dfrac{\sqrt{a^2-x^2}}{a} cost=aa2−x2
∫ a 2 − x 2 d x = a 2 2 ( arcsin x a + x a a 2 − x 2 a ) + C = a 2 2 arcsin x a + x 2 a 2 − x 2 + C \displaystyle \int \sqrt{a^2-x^2}dx =\dfrac{a^2}{2}(\arcsin{\dfrac{x}{a}}+\dfrac{x}{a}\dfrac{\sqrt{a^2-x^2}}{a})+C =\dfrac{a^2}{2}\arcsin{\dfrac{x}{a}}+\dfrac{x}{2}\sqrt{a^2-x^2}+C ∫a2−x2dx=2a2(arcsinax+axaa2−x2)+C=2a2arcsinax+2xa2−x2+C -
【代换2】
∫ x 2 − a 2 x d x ( a > 0 ) \displaystyle \int \dfrac{\sqrt{x^2-a^2}}{x}dx \quad (a>0) ∫xx2−a2dx(a>0)
令 x = a sec t x=a\sec{t} x=asect, t ∈ ( − π / 2 , π / 2 ) t \in (-\pi/2,\pi/2) t∈(−π/2,π/2),则
∫ x 2 − a 2 x d x = ∫ a tan t a sec t d x = ∫ sin t a sin t cos 2 t d t = a ∫ tan 2 t d t = a ∫ ( sec 2 t − 1 ) d t = a tan t − a t + C \displaystyle \int \dfrac{\sqrt{x^2-a^2}}{x}dx =\displaystyle \int \dfrac{a\tan{t}}{a\sec{t}}dx =\displaystyle \int \sin{t}\dfrac{a\sin{t}}{\cos^2{t}}dt =a\displaystyle \int \tan^2{t}dt =a\displaystyle \int (\sec^2{t}-1)dt =a\tan{t}-at+C ∫xx2−a2dx=∫asectatantdx=∫sintcos2tasintdt=a∫tan2tdt=a∫(sec2t−1)dt=atant−at+C
由 sec t = x a \sec{t}=\dfrac{x}{a} sect=ax,有 cos t = a x \cos{t}=\dfrac{a}{x} cost=xa,得 t = arccos a x t=\arccos{\dfrac{a}{x}} t=arccosxa
∫ x 2 − a 2 x d x = a x 2 − a 2 a − a arccos a x + C = x 2 − a 2 − a arccos a x + C \displaystyle \int \dfrac{\sqrt{x^2-a^2}}{x}dx =\dfrac{a\sqrt{x^2-a^2}}{a}-a\arccos{\dfrac{a}{x}}+C =\sqrt{x^2-a^2}-a\arccos{\dfrac{a}{x}}+C ∫xx2−a2dx=aax2−a2−aarccosxa+C=x2−a2−aarccosxa+C -
【代换3】
∫ 1 a 2 + x 2 d x ( a > 0 ) \displaystyle \int \dfrac{1}{\sqrt{a^2+x^2}}dx \quad (a>0) ∫a2+x21dx(a>0)
令 x = a tan t x=a\tan{t} x=atant, t ∈ ( − π / 2 , π / 2 ) t \in (-\pi/2,\pi/2) t∈(−π/2,π/2),则
∫ 1 a 2 + x 2 d x = ∫ 1 a sec t d x = ∫ 1 a sec t a sec 2 t d t = ∫ sec t d t = ln ∣ sec t + tan t ∣ + C \displaystyle \int \dfrac{1}{\sqrt{a^2+x^2}}dx =\displaystyle \int \dfrac{1}{a\sec{t}}dx =\displaystyle \int \dfrac{1}{a\sec{t}}a\sec^2{t}dt =\displaystyle \int \sec{t}dt =\ln{|\sec{t}+\tan{t}|}+C ∫a2+x21dx=∫asect1dx=∫asect1asec2tdt=∫sectdt=ln∣sect+tant∣+C
由 tan t = x a \tan{t}=\dfrac{x}{a} tant=ax,得 sec t = a 2 + x 2 x \sec{t}=\dfrac{\sqrt{a^2+x^2}}{x} sect=xa2+x2
∫ a 2 − x 2 d x = ln ∣ a 2 + x 2 x + x a ∣ + C = ln ∣ a 2 + x 2 + x ∣ + C − ln a = ln ∣ a 2 + x 2 + x ∣ + C \displaystyle \int \sqrt{a^2-x^2}dx =\ln{|\dfrac{\sqrt{a^2+x^2}}{x}+\dfrac{x}{a}|}+C =\ln{|{\sqrt{a^2+x^2}}+{x}|}+C-\ln{a} =\ln{|{\sqrt{a^2+x^2}}+{x}|}+C ∫a2−x2dx=ln∣xa2+x2+ax∣+C=ln∣a2+x2+x∣+C−lna=ln∣a2+x2+x∣+C
3.出错点
【dx和dt的转化方向错误】
x = a sin t x=a\sin{t} x=asint
正确:对x求导
∫ d x = ∫ x ′ d x = ∫ a cos t d t \displaystyle \int dx =\displaystyle \int x'dx =\displaystyle \int a\cos{t}dt ∫dx=∫x′dx=∫acostdt
错误:对t求导
∫ d x → ∫ t ′ d x = ∫ ( arcsin x a ) ′ d t \displaystyle \int dx \to \displaystyle \int t'dx =\displaystyle \int (\arcsin{\dfrac{x}{a}})'dt ∫dx→∫t′dx=∫(arcsinax)′dt
4.题
(1)第二类换元法的基本应用
(2)难题
- ∫ 1 + e x d x \displaystyle \int \sqrt{1+e^x}dx ∫1+exdx
令 t = 1 + e x t=\sqrt{1+e^x} t=1+ex,则 x = ln ( t 2 − 1 ) x=\ln{(t^2-1)} x=ln(t2−1)
∫ 1 + e x d x = ∫ t d x = ∫ t 1 t 2 − 1 2 t d t = ∫ 2 t 2 t 2 − 1 d t = ∫ 2 ( t 2 − 1 ) + 2 t 2 − 1 d t = ∫ ( 2 + 2 t 2 − 1 ) d t = 2 t + 2 ∫ 1 t 2 − 1 d t = 2 t + 2 ln ∣ t − 1 t + 1 ∣ + C = 2 1 + e x + 2 ln ∣ 1 + e x − 1 1 + e x + 1 ∣ + C \displaystyle \int \sqrt{1+e^x}dx =\displaystyle \int tdx =\displaystyle \int t\dfrac{1}{t^2-1}2tdt =\displaystyle \int \dfrac{2t^2}{t^2-1}dt =\displaystyle \int \dfrac{2(t^2-1)+2}{t^2-1}dt =\displaystyle \int (2+\dfrac{2}{t^2-1})dt =2t+2\displaystyle \int \dfrac{1}{t^2-1}dt =2t+2\ln|{\dfrac{t-1}{t+1}}|+C =2\sqrt{1+e^x}+2\ln|{\dfrac{\sqrt{1+e^x}-1}{\sqrt{1+e^x}+1}}|+C ∫1+exdx=∫tdx=∫tt2−112tdt=∫t2−12t2dt=∫t2−12(t2−1)+2dt=∫(2+t2−12)dt=2t+2∫t2−11dt=2t+2ln∣t+1t−1∣+C=21+ex+2ln∣1+ex+11+ex−1∣+C
三、分部积分法
1.公式
∫ u d v = u v − ∫ v d u \displaystyle \int udv=uv-\displaystyle \int vdu ∫udv=uv−∫vdu
∫ u v ′ d x = u v − ∫ v u ′ d x \displaystyle \int uv'dx=uv-\displaystyle \int vu'dx ∫uv′dx=uv−∫vu′dx
2.解析
- ∫ ln x ( 1 − x ) 2 d x \displaystyle \int \dfrac{\ln{x}}{(1-x)^2}dx ∫(1−x)2lnxdx
令 u = ln x , v = 1 1 − x ( ∫ ln x ( 1 − x ) 2 d x = ∫ ln x ( 1 1 − x ) ′ d x ) u=\ln{x},v=\dfrac{1}{1-x} \quad (\displaystyle \int \dfrac{\ln{x}}{(1-x)^2}dx=\displaystyle \int \ln{x} (\dfrac{1}{1-x})'dx) u=lnx,v=1−x1(∫(1−x)2lnxdx=∫lnx(1−x1)′dx)
= ln x 1 − x − ∫ 1 x ( 1 − x ) d x = ln x 1 − x − ∫ ( 1 x + 1 1 − x ) d x = ln x 1 − x + ln ∣ 1 − x ∣ x + C =\dfrac{\ln{x}}{1-x} - \displaystyle \int \dfrac{1}{x(1-x)}dx =\dfrac{\ln{x}}{1-x} - \displaystyle \int (\dfrac{1}{x} +\dfrac{1}{1-x})dx =\dfrac{\ln{x}}{1-x} + \ln{\dfrac{|1-x|}{x}}+C =1−xlnx−∫x(1−x)1dx=1−xlnx−∫(x1+1−x1)dx=1−xlnx+lnx∣1−x∣+C