2023.2.5 第三十九次周报

目录

前言

文献阅读：基于RNN方法的时间卷积网络用于混沌时间序列预测 

背景

主要思路

方法论

时间卷积网络

递归神经网络

支持向量机（SVM）

SVM直觉理解

 升维转换和核技巧（Kernel Trick）

求解SVM决策超平面

总结

---

前言

This week I learned an article that proposed a hybrid deep neural network architecture for chaotic time series forecasting.The hybrid methods used include temporal convolutional networks and recurrent neural network layers that extract low-level features from inputs, such as long short-term memory and gated recurrent units to capture temporal information.In addition, in terms of machine learning, I learned some support vector machines.

本周学习了一篇文章，该文提出一种用于混沌时间序列预测的混合深度神经网络架构。使用的混合方法包括从输入中提取低级特征的时间卷积网络和循环神经网络层，例如长短期记忆和门控循环单元以捕获时间信息。除此之外，在机器学习方面，学习了一些支持向量机的相关内容。

文献阅读：基于RNN方法的时间卷积网络用于混沌时间序列预测 

——Hatice Vildan Dudukcu, Murat Taskiran, Zehra Gulru Cam Taskiran, Tulay Yildirim,
Temporal Convolutional Networks with RNN approach for chaotic time series prediction,
Applied Soft Computing,
Volume 133,
2023,
109945,
ISSN 1568-4946,
https://doi.org/10.1016/j.asoc.2022.109945.

背景

构成科学和工程领域许多系统的混沌时间序列的预测，最近成为研究人员关注的焦点。混沌时间序列预测是使用先前观察到的数据对具有已知初始条件的非线性混沌系统进行未来预测。混沌时间序列预测可以应用于许多领域，如天气预报、金融和股票市场。许多学科致力于解决时间序列预测问题，从提前几天预测天气事件到交易者预测股票的未来。在最近的研究中，已经观察到混合深度神经网络方法在解决时间序列预测问题方面具有更好的性能，并且已经普及，以便从多种方法在解决此类问题方面的优势中受益。该文提出一种用于混沌时间序列预测的混合深度神经网络架构。使用的混合方法包括从输入中提取低级特征的时间卷积网络和循环神经网络层，例如长短期记忆和门控循环单元以捕获时间信息。

主要思路

本研究提出了一种由不同神经网络层、时间卷积神经网络（TCN）与循环神经网络（RNN）组合而成的混合模型。在模拟研究中，使用从Lorenz，Rössler和Lorenz类方程集中获得的三个不同的数据集，以及将21个心律失常患者的心电记录的真实混沌数据集转介到波士顿贝斯以色列医院的心律失常实验室，将所提出的方法与经典ML结构和深度学习方法进行了比较，可以看出所提出的模型实现了最低的预测RMSE值。

方法论

混沌时间序列的预测已成为最近研究人员最感兴趣的话题之一。由于对混沌时间序列的预测，可以预测许多在自然界中表现出动态行为的系统。与经典的循环神经网络相比，混合使用不同的神经网络结构可以为预测问题提供更好的结果，这一事实导致了当前对这些方法的研究。该文提出由TCN、LSTM和GRU层组成的RNN架构TCN来解决混沌时间序列预测问题。该架构由 TCN 和 RNN 层组成。TCN有助于提取短时间内发生的变化特征，而LSTM揭示了长时间内发生的变化的特征，GRU具有有效的非线性拟合能力[48]，[51]。通过这种方式，可以对分布在宽频谱上的所有特征进行建模。在所使用的模型中，TCN提取时间序列的一维空间特征，并将这些特征向量提供给RNN。两个网络一起训练，从而获得两轮特征提取和两轮数据杂质过滤。由于 TCN 已经大大减少了数据杂质，因此尾随 RNN 阶段更有效地工作并更好地提取顺序特征。

本研究提出了一种混合方法，包括时间卷积神经网络和循环神经网络，用于时间序列预测。在检查时间序列预测文献时，值得注意的是，TCN架构在解决大多数预测问题方面比LSTM和GRU表现更好，并且在大多数研究中已经研究了有多少堆叠的TCN层提供了最佳结果。由于TCN的结构，随着层数的增加，卷积层的计算负荷增加，模型并不总是给出更成功的结果。在本研究提出的混合结构中，TCN被用作第一个DNN层，以提取宽感受野中的低级特征。特征的时间信息，即TCN层的输出，在下一步中与RNN层进行处理，以充分利用混沌时间序列。该研究提出了两种不同的混合方法。如图所示，这些方法中的第一种方法是在 TCN 层的输出中使用 LSTM 和密集层进行预测的方法，第二种方法包括 GRU 和具有 TCN 的密集层进行预测。在这项研究的范围内，使用TCN层将数据转换为模式，然后使用RNN层的记忆门将模式传输到未来时间，从而提高了时间序列的预测性能。

                                                图 ：TCN-RNN的混合方法。 

时间卷积网络

时间卷积网络（TCN）是一种深度学习架构，具有用于1D数据的扩展，因果一维卷积层。Lea等人在2016年首次使用这种架构来执行基于视频的动作分割，并且它扩大了计算低级特征的CNN层。TCN 适用于利用 CNN 输出作为输入来捕获时态信息的 RNN 模型。与RNN相比，TCN中的扩张CNN层可以通过使用较大的感受野从更长的时间序列中提取特征。与RNN模型相比，TCN的缺点是计算成本更高，训练时间更长。

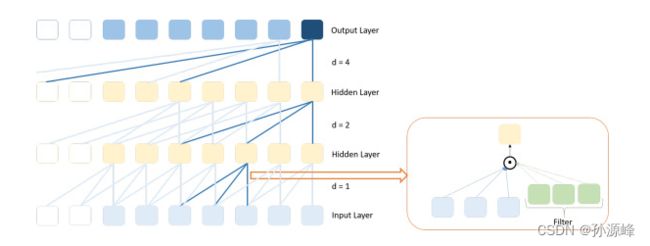
图 1 中给出的 TCN 架构由具有扩张卷积层、归一化、激活和辍断层的残差块以及可选的 1 × 1 卷积组成，当残差输入和输出具有不同维度时使用。在膨胀卷积层中，对于每个隐藏向量，根据输入值和滤波器卷积计算相关的隐藏单元值。通过使用计算出的隐藏向量，通过膨胀计算创建下一个隐藏层的向量，并在最后一个膨胀层中获得输出向量。图2给出了使用膨胀层从输入向量输出向量的计算过程。

                                                           图 1.TCN 架构 

                        图 2.扩张卷积，膨胀因子d = 1，2，4，使用过滤器尺寸3  

递归神经网络

递归神经网络（RNN）架构是文献中广泛用于预测的深度学习结构，由于内部的内存连接，它可以学习并通过过去信息的推断进行预测。尽管经典的RNN结构在预测短期数据中给出了成功的结果，但由于在长期数据问题中遇到的梯度消失问题，它们没有用。已经提出了具有不同记忆连接的RNN结构，例如门控循环单元（GRU）和长短期记忆（LSTM）来解决这个问题。最近，这两种架构比经典的RNN方法更常用于预测问题。

长短期记忆（LSTM）是一种用于深度学习领域的递归神经网络（RNN）架构。与标准的前馈神经网络不同，LSTM具有反馈连接和内存状态，其中存储了网络的先前输出。除了即时数据，它还可以处理数据序列，因此经常用于解决预测问题。在 LSTM 深度学习架构中，如图 3 所示，每个单元接收一个单元状态 （ct−1）、隐藏状态 （ht−1） 和输入 （xt） 作为时间步长 t，并创建一个单元格状态 （ct） 和隐藏状态 （ht） 在单元格输出。在这里，隐藏状态表示单元的输出，单元状态表示包含有关先前时间步长的信息的存储行。

门控循环单元（GRU）是一种简化和改进的LSTM结构类型，具有两个门，称为复位和更新门。单元格在给定时间的输入为 xt前一个单元格的输出为 ht−1.在GRU结构中，通过组合图3所示的细胞状态和隐藏状态来创建单个单元输出，并且过去的信息通过计算的单元输出（ht).

                                       图 3.LSTM 和 GRU 架构比较 

支持向量机（SVM）

SVM直觉理解

在这种画法中，两类数据中所有的点，都与决策边界线保持了一定的距离。这个距离起到了缓冲区的作用。当这个缓冲区足够大时，分类结果的可信度就更高了。我们把这个缓冲区称为间隔（Margin），这个间隔把两类数据所处的空间分隔开来，间隔距离可以体现出两类数据的差异大小。越大的间隔，意味着两类数据差异越大，那么我们区分起来就越容易。因此寻找最佳决策边界线的问题可以转化为，求解两类数据的最大间隔问题。而间隔的正中就是我们的决策边界。当有新数据需要判断时，根据它处于决策边界的相对位置，我们就可以进行分类了。

 假设决策边界的超平面方程式为W1X1+W2X2+b=0,它向上下分别移动C，来到对应的间隔上下边界，由于上下边界一定会经过一些样本数据点，而这些点距离决策边界最近，他们决定了间隔距离，我们称它们为支持向量 Support vector，这也是为什么我们将该方法命名为支持向量机。最终由上图得到了三个超平面方程式。正超平面，决策超平面，负超平面。所有正超平面及其上方的数据点颜色相同，都属于正类。负超平面及其下方的点为负类。当有新数据加入，需要我们分类判断时，我们则可以利用它与决策超平面的相对位置进行分类。

 

 升维转换和核技巧（Kernel Trick）

对于在低维度下无法方便分类上的数据，我们就可以采用类似的方法：

1.通过合适的维度转换函数，将低维度进行升维

2.在高维度下求解SVM模型，找到对应分隔超平面

当有新数据需要进行分类预测时，可以对其先做升维转换操作，再根据高维度下的决策边界超平面进行判断。

不过提升维度，你需要明确的维度转换函数，以及更多的数据存储，计算需求。那么有没有一种方法能够避免将数据送入高维度进行计算，却又能获得相同的分类效果呢？那么我们就需要运用Kernel Trick 核技巧了。由于SVM的本质是量化两类数据差异的方法，而核函数Kernel Function能够提供高维度向量相似度的测量。通过选取合适的核公式，我们就可以不用知晓具体的维度转换函数，直接获得数据的高维度差异度，并以此来进行分类判断。

求解SVM决策超平面

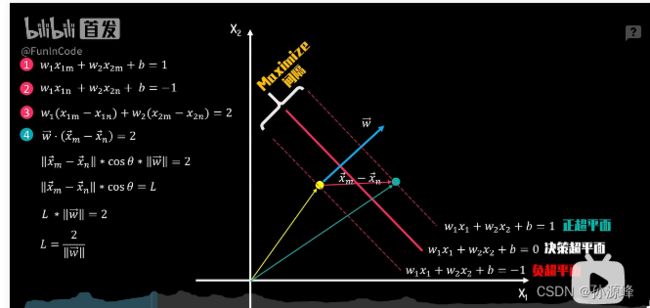
还是先以二维数据为例，我们的目标是最大化正负超平面的间隔距离L。那么构建L的表达式就非常重要了，我们分别在正负超平面上随机选取一个支持向量点X_m和X_n。由于它们都位于正负超平面上，所以满足超平面等式1，2。用等式1减去等式2可以得到等式3，等式3可以理解为向量w和向量x_m-x_n的点积结果为2。

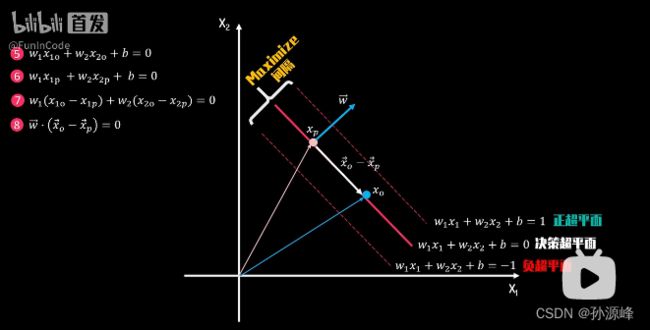
 在决策超平面上随机选择两个点o,p他们满足等式5，6。我们用等式5减去等式6得到等式7，它可以理解为向量w和向量（x_o-x_p）的点积结果为0.因为向量的点积结果为两个向量的长度相乘，再乘以他们之间的夹角的cos值。当点积结果为零时意味着两向量的夹角为90°，两向量垂直，所以点积结果可以反映出向量的相似性。当结果为正时，两者的方向具有相似性；当点积结果为0，两向量垂直；点积结果为负时，两向量方向背离。根据等式8，本例中向量w和向量（x_o-x_p）垂直，由于向量x_o-x_p就处于决策边界上，因此我们可以得到向量w与决策超平面垂直。

 

现在再回到等式4，我们已知向量w与决策超平面垂直，向量x_m-x_n与之的点积就可以等价于向量x_m-x_n的长度乘以向量w的长度，再乘以两者的夹角cosθ为向量x_m-x_n投影到向量w上的长度，也就是我们要求的正负超平面间隔距离L。我们最后可以得到间隔距离L的表达式，由于我们需要最大化L，这等同于求解在约束条件下，向量w长度的最小化问题。

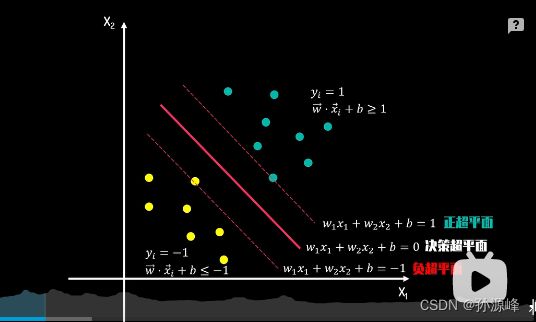
我们现在来看约束条件，所有绿点都属于正类，对应的分类值y=1,又因为它们处于正超平面上或位于其上方，所以wx_i+b>=1;同样的所有的黄点属于负类，对应分类值y=-1，满足约束条件wx+b<=-1。从以上约束条件中我们可以归纳出下面两点：

1.约束表达式均为仿射函数约束。

2.约束表达式可以进一步提炼为y*(wx+b)>=1

 这是一个在仿射函数约束下的凸优化问题，我们知道如果约束条件是等式的话，我们可以直接使用拉格朗日乘子法求解。但如果约束条件是不等式，我们需要进行一些变化，通过增加一个非负变量p_i的平方，将不等式转化为等式约束，再使用拉格朗日乘子法。

为了求上述方程式的极值，我们对这些参数分别求偏导，其值均为0得到等式1~4.我们把等式4左右两边分别除以2再乘p_i，再将约束条件3带入等式4，得到新的等式4。根据约束条件，括号内的值非负，那么满足新等式4成立只有两种可能性：

1.括号内的值大于0，这意味着对应数据点不在正负超平面上，此时λi必须等于0

2.括号内的值等于零，此时λi可以不为0

总结

 下周继续学习和讨论SVM的数学推导以及其他知识。