【SDOF振荡器的非线性-非弹性多轴时间响应分析】用于SDOF振荡器非线性非弹性时程分析的鲁棒性分析研究（Matlab代码实现）

 欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

3 参考文献

4 Matlab代码实现

---

1 概述

进行SDOF振荡器的非线性非弹性时程分析的鲁棒性分析研究，旨在探究该方法对不同系统参数和分析条件变化的稳定性和可靠性。以下是一些可能的研究内容和方法：

1. 参数变化对结果的影响：通过对系统参数进行变化，例如刚度、阻尼、质量等，观察这些参数变化对非线性非弹性时程分析结果的影响。可以分析参数变化对振动响应的幅值、频谱特性、时程历程等的影响，进而评估该方法的稳定性和准确性。

2. 非线性模型的复杂度：考虑不同程度的非线性，比如线性衰减、非线性阻尼、非线性刚度等，并对这些模型进行时程分析。通过对比不同非线性程度下的振动响应结果，评估方法对于复杂非线性模型的鲁棒性。

3. 非线性耦合效应：对于涉及多个非线性项的情况，如非线性刚度和非线性阻尼同时存在的振动系统，研究该方法对于非线性耦合效应的处理能力。通过引入不同程度的耦合效应，分析其对时程分析结果的影响，进而评估方法的鲁棒性。

4. 数值方法的稳定性：对于非线性非弹性时程分析方法使用的数值方法，如数值积分算法，进行稳定性研究。通过修改数值方法的步长、积分算法等参数，观察这些参数变化对求解结果的影响，评估方法的稳定性和可靠性。

5. 算法对比分析：将SDOF振荡器的非线性非弹性时程分析方法与其他数值方法进行对比，例如频域方法、步进法等，比较它们的优劣和鲁棒性。可以选取不同的振动系统和不同的分析条件，通过对比结果的准确性和收敛性来评估方法的鲁棒性。

通过以上鲁棒性分析研究，可以对SDOF振荡器的非线性非弹性时程分析方法在不同情况下的适用性和可靠性进行评估，提供工程实际应用的指导和建议。

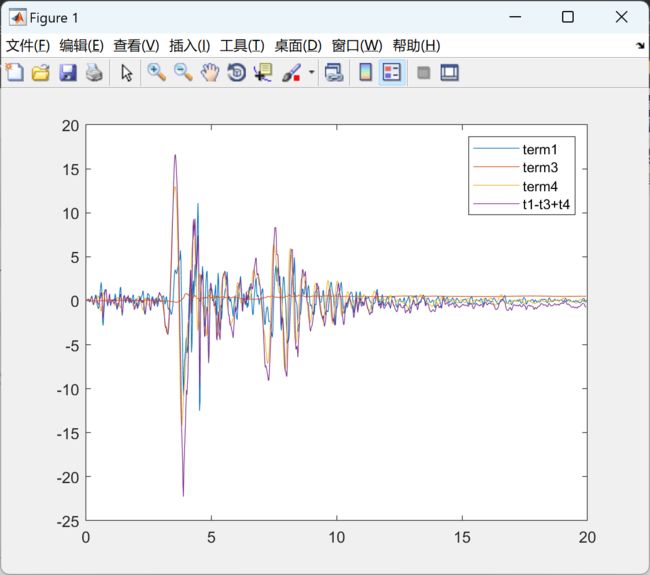
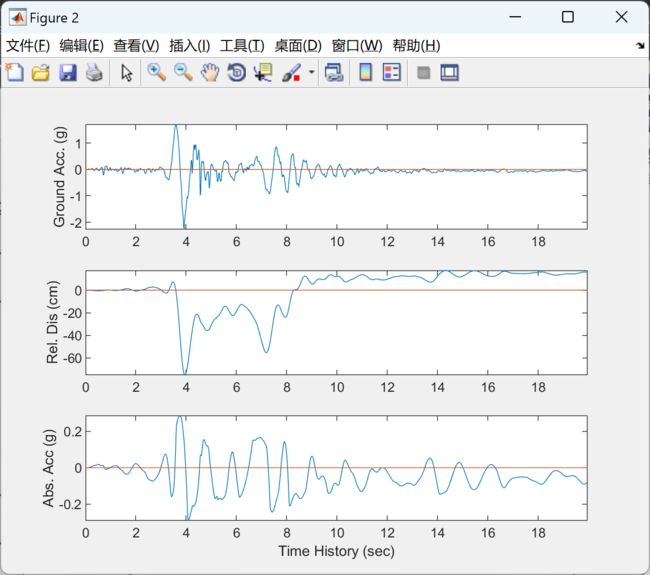
强大的 MatLAB 功能，用于对 SDOF 振荡器进行非线性非弹性时程分析，该振荡器承受多轴同时激励，包括水平、垂直和旋转运动。它还计算传递给SDOF振荡器的地震输入能量的分量。
主要特点是：

- 多轴激励 - 材料非线性由Ozdemir的速率无关力-位移模型
表示 - 包括
P-Delta（全局水平）
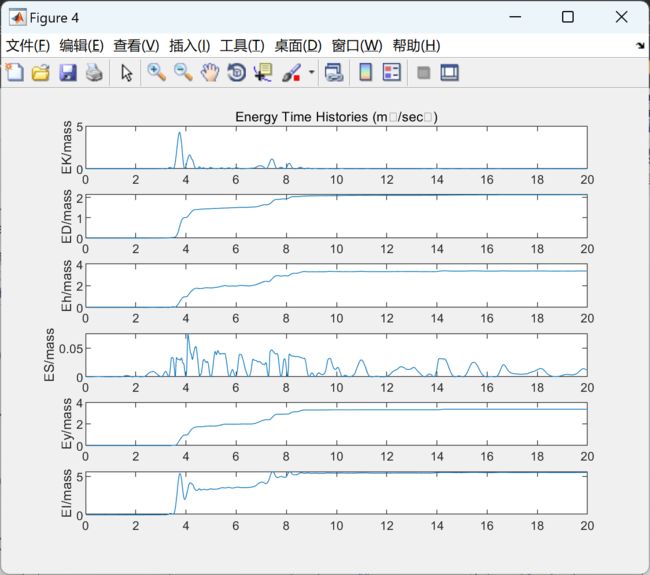
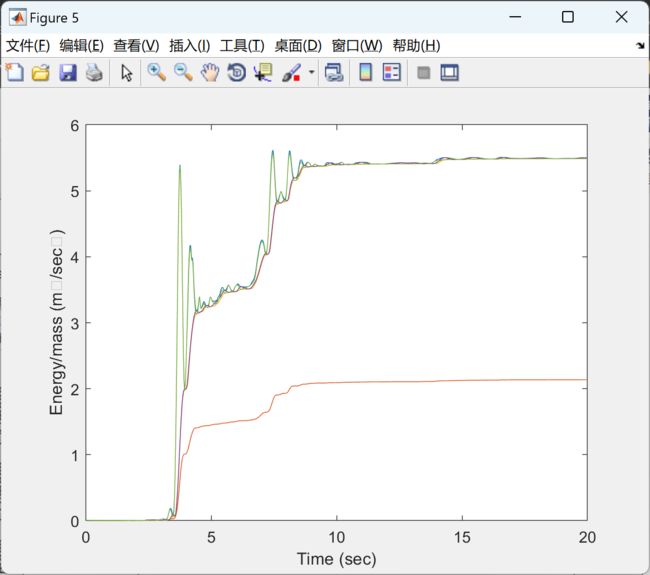
- 绝对和相对能量分量计算

2 运行结果

 

 

 

 

 

部分代码：

Tn = 1.2;           % Natural period (sec)
omegan = 2*pi/Tn;    % Natural frequency (rad/sec)
xi = 0.05;           % Damping ratio
g = 9.81;            % Gravity constant (m/sec�)
%fy = 0.2533*g;      % Yield force (normalized by mass which is already 1.0) 
ky = 2.40;          
%uy = ky/omegan^2;    % Yield displacement (m)
uy = 0.0523
alpha = 0.02;        % Post to pre-yielding stiffness ratio
eta = 21;            % Elastic to inelastic transition parameter
l = 9;               % Length of oscillator (m) (if it is too large, small geometric stiffness term)

Kg = g/l;            % Geometric stiffness term (1/sec�)
Tg = 2*pi*(1/Kg)^.5; % Static geometric oscillation period (sec) see ASCE paper by Kalkan & Graizer (2007)

dt = 0.02;           % Time step of ground acceleration (sec)
[gacc gaccZ gaccH term3 term4] = groundMotionData(l,g,dt);    % Call ground motion input data function

% Assign values to integration variables 

N = length(gacc);    % Number of points
td = N*dt;           % Duration of ground motion
tspan = (dt:dt:td);  % Time vector (sec)
y1o = 0;             % Initial value of y1
y2o = 0;             % Initial value of y2
y3o = 0;             % Initial value of y3
y4o = 0;             % Initial value of y4
y5o = 0;             % Initial value of y5
yo = [y1o;y2o;y3o;y4o;y5o];  % Initial conditions for state vector

% Call ODE solver to solve system of first-order ODE's
% (Use a stiff solver since the euqations are nonlinear)

[t,y] = ode15s('nonlinsysMultiAxial',tspan,yo,[],omegan,xi,gacc,tspan,uy,alpha,eta,td,Kg,gaccZ,l,dt);

% Extract response from state vector
% (Note that the output of the ODE solver is the state vector y)
% in which yi as a function of time is in the i-th column

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]Dr. Erol Kalkan, P.E. (2023). NONLINEAR-INELASTIC MULTI-AXIAL TIME RESPONSE ANALYSIS OF SDOF OSCILLATOR.

[2]Yaghmaei-Sabegh S,Daneshgari S.Effect of ground motion duration on inelastic displacement ratio of SDOF systems[J].Earthquake Engineering and Engineering Vibration,2023,22(02):423-439.

[3]侯红梅,刘文锋,张怀超.基于SDOF体系和高层结构的地震动强度指标研究[J].地震工程学报,2021,43(06):1436-1443.

4 Matlab代码实现