卷积神经网络参数量和计算量的计算方法

本文总结了标准卷积、分组卷积和全连接层参数量和计算量的计算方法，如有错误，麻烦大家指正

一、标准卷积

假设输入特征的shape为[, , ]，卷积核的shape为[, , , ]，输出特征的shape为[, , ]，则，

标准卷积运算的参数量为：

• 不考虑bias：
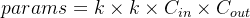
• 考虑bias：

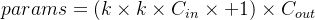
标准卷积运算的计算量为：

• 不考虑bias：
• 考虑bias：

二、深度可分离卷积

假设输入特征的shape为[, , ]，卷积核的shape为[, , , , ]（g为分组数量），输出特征的shape为[, , ]，则，

分组卷积运算的参数量为：

• 不考虑bias：
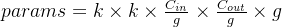
• 考虑bias：

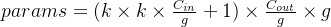
分组卷积运算的计算量为：

• 不考虑bias：
• 考虑bias：

举个栗子，假设输入特征的shape为[1,3,6,6]，卷积的shape为[3,6,3,3]，分组卷积的g为3，输出特征的shape为[1,6,2,2]，则，标准卷积的计算量=[(3*3*3)+(3*3*3-1)+1]*2*2*6=1296，分组卷积的计算量=[(3*3*3)+(3*3*3-1)+1]*2*2*6/3*3=1296/3=432。下面使用thop验证一下，

import torch
import torch.nn as nn
from torchstat import stat
from thop import profile


x = torch.randn((1,3,6,6))
conv1 = nn.Conv2d(3,6,3,3)
conv2 = nn.Conv2d(3,6,3,3,groups=3)
flops1, params1 = profile(conv1, inputs=(x))
print(flops1)
print("自测:", (3*3*3+3*3*3-1+1)*6*2*2)
flops2, params2 = profile(conv2, inputs=(x))
print(flops2)
print("自测:", ((3*3*1+3*3*1-1+1)*6*2*2))


"""
[INFO] Register count_convNd() for .
1296.0
自测: 1296
[INFO] Register count_convNd() for .
432.0
自测: 432
"""

深入思考一下，经过标准卷积层后，输出特征图上的每一个点都由计算得来。而如果经过的是分组卷积层，那么输出特征图上的每一个点则由计算得来。因此，分组卷积的参数量为标准卷积参数量的

然而，由于深度卷积的FLOPs与内存访问的比率太低，难以有效利用硬件，所以只是理论上比标准卷积的计算要快

三、全连接层

假设全连接层的shape为[, ]，则，

全连接层的参数量为：

• 不考虑bias：
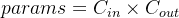
• 考虑bias：

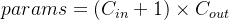
全连接层的计算量为：

• 不考虑bias：
• 考虑bias：