【论文精读】FSUIE: A Novel Fuzzy Span Mechanism for Universal Information Extraction

前言

一篇来自ACL 2023的工作，有关通用信息抽取模型的内容，这里并没有使用当前火爆的指令微调生成式大模型的方法来抽取信息，而是在基于最简单的bert模型，在损失函数和attention机制上做文章，是一篇非常值得借鉴的工作。

---

Paper: https://arxiv.org/pdf/2306.14913.pdf
Code: https://github.com/pengts/fsuie

Abstract

现有的UIE模型严重依赖边界跨度，即模型对数据边界标注错误十分敏感，并且很少关注抽取跨度长度的特征，本文提出了模糊跨度通用信息抽取框架（FSUIE），具体包括两个部分：模糊跨度损失和模糊跨度注意力。实验部分证明模型在收敛速度和小样本场景表现出色。

1. Introduction

信息抽取专注于从非结构化文本中抽取结构化信息，如命名实体识别，关系抽取，情感抽取。通用信息抽取是在统一框架下对上述任务进行建模，生成式模型时间开销大且效果不理想，本文研究了基于跨度的UIE以统一各种IE任务，将IE任务转化为跨度预测。

但是UIE模型仍有如下的限制：

1. 依赖人工标注信息和跨度（见上图），但是人工标注容易产生歧义。
2. 跨度学习任务上，损失函数采用教师强制方法， 容易因为注释不准确造成性能瓶颈。
3. 模型过于强调精确边界，会导致监督信息利用不足，事实上有些跨度就是模糊的，如上图所示，“汽车”、“跑车”、“黄色跑车”都是同一个实体。
4. 预训练模型和跨度提取在任务上不一致，前者关注所有的文本，后者关注特定文本。

本文提出FSUIE，通过应用模糊跨度特征和调整注意力机制跨度来解决上述限制。具体来说，设计了模糊跨度损失定量表示分布在模糊跨度上的准确性，以及模糊跨度注意力，将注意力范围设置为模糊范围，根据编码自适应调整跨度的长度。实验部分，仅使用bert-base模型就达到了NER、RE和ASTE基准测试的SOTA，并且具有收敛速度快、小样本场景泛化能力好等特性。

2. FSUIE

2.2 Fuzzy Span Loss (FSL)

FSL是对传统的教师损失（交叉熵）的补充，指导模型学习模糊边界。挑战在于如何量化模糊边界中正确信息的分布。传统的分布只关注准确的边界，本文提出了模糊跨度分布生成器（FSDG），使用跨度边界的概率分布来表示真实值，包括两个步骤：

1. 确定概率密度分布函数$f$。
2. 基于$f$将连续分布映射到离散分布。

具体来说，让$q\in S$作为标签跨度的边界， 则其对应模糊边界的期望为：
$$\hat{q}={\int }_{R_{min}}^{R_{max}}xQ(x)dx,q\in S$$
其中$x$表示模糊边界范围$[R_{min},R_{max}]$内的坐标，$R_{min}$和$R_{max}$是模糊坐标的起始和结束位置。$q^{gt}$代表边界真实位置，$Q(x)$表示对应位置的概率。
通过映射函数$F$可以将模糊的连续边界映射为离散边界，每个给定边界的概率分布可以通过softmax函数结果表示。
FSUIE选择高斯分布$N(\mu .{\sigma }^2)$作为概率密度函数$f$，其优点为：

1. 连续且对称。
2. 峰值小、偏移量少，分布集中稳定。
3. 积分为1（凑出来的理由。。。）。

为了得到离散值$\hat{\mathbf{q}}$，需要四个参数：方差$\sigma$、均值$\mu$、采样步骤$s$以及采样阈值$\theta$。这些参数分别控制模糊边界的范围、峰值位置和密度。具体来说，均值设定为$q^{gt}$，方差为预定义，$F$可以表示为：
$$\begin{array}{l}F\left(q_i\right)=\{\begin{array}{ll}\epsilon ,& \epsilon \ge \theta \\ 0,& \epsilon <\theta \end{array},\\ \epsilon =f(\mu +(i-g)s)\end{array}$$
$\theta$用于过滤掉高斯分布边缘区域的值，因为它们的概率非常低。接着，计算模型的预测logits和核心模糊跨度分布的KL散度作为模糊跨度损失。下图显示了准确分布和模糊分布的边界。

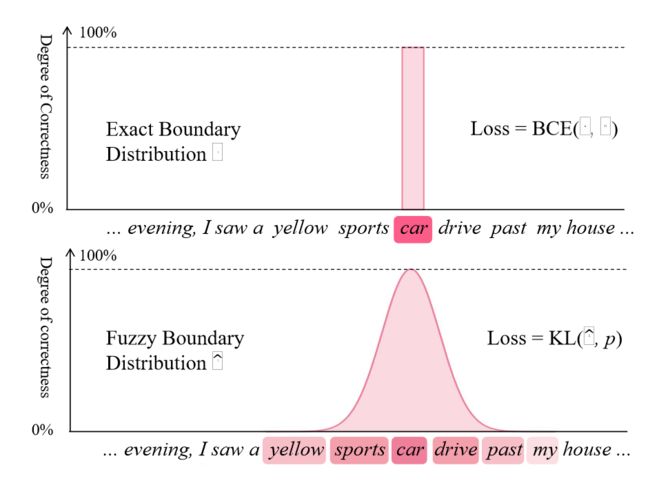
然后将模糊跨度损失并入原始的损失函数中，如下：
$$\begin{array}{rl}{\mathcal{L}}_{FS}=D_{KL}(\hat{\mathbf{q}}\Vert p)& =\sum _{i=1}^N\hat{\mathbf{q}}\left(x_i\right)\left(\log \frac{\hat{\mathbf{q}}\left(x_i\right)}{p\left(x_i\right)}\right)\\ \mathcal{L}& ={\mathcal{L}}_{\text{ori }}+\lambda {\mathcal{L}}_{FS}\end{array}$$
其中，$p$表示模型的预测分布，$\hat{\mathbf{q}}$表示生成的模糊跨度分布，$\lambda$表示模糊跨度损失的系数。

2.2 Fuzzy Span Attention (FSA)

作者基于具有相对位置编码（RPE）的多头自注意力机制构建了FSA。对于序列中位置$t$的token，每个头计算该token与序列中token的相似度矩阵。token $t$和token $r$之间的相似度可以表示为：
$$s_{tr}=y_t^{\top }{W}_q^{\top }(W_k{y}_r+p_{t-r})$$
其中，$W_k$和$W_q$是key和query的权重，$y_t$和$y_r$是token $t$和token $r$的表示，$p_{t-r}$是相对位置embedding。通过softmax函数可以得到对应的attention权重：
$$a_{tr}=\frac{\exp (s_{tr})}{{\sum }_{q=0}^{t-1}\exp (s_{tq})}$$
FSA的模糊跨度机制包括两个方面：

1. 动态调整全注意力范围的长度。
2. 整个注意力跨度边界上的注意力权重会衰减而不是直接截断。

具体来说，作者设计了一个掩码函数$g_m$来控制注意力分数计算，假设可能的注意力跨度最大长度为$L_{span}$，新的注意力得分可以表示为：
$$a_{tr}=\frac{g_m(t-r)\exp \left(s_{tr}\right)}{{\sum }_{q=t-L_{span}}^{t-1}{g}_m(t-r)\exp \left(s_{tq}\right)}$$
过程可以分为两个阶段：

1. 确定模糊边界注意力变化函数$g_a$。
2. 基于$g_a$构建掩码函数$g_m$以进行跨度感知表示学习。

为了调整注意力跨度长度，作者定义了一个可学习的参数$\delta \in [0,1]$。$g_a(x)$和对应的$g_m(x)$可以表示如下：
$$\begin{array}{rl}& g_a(z)=\frac{-z+l+d}{d},\\ & l=\delta L_{\text{span }}.\\ & g_m(z)=\{\begin{array}{ll}1,& g_a(z)>1\\ 0,& g_a(z)<0\\ g_a(z),& \text{ otherwise }\end{array}\\ & \end{array}$$
其中$l$控制完整注意力范围长度，$d$是控制衰减注意力范围长度的超参数。下图是$g_m$函数的描述：

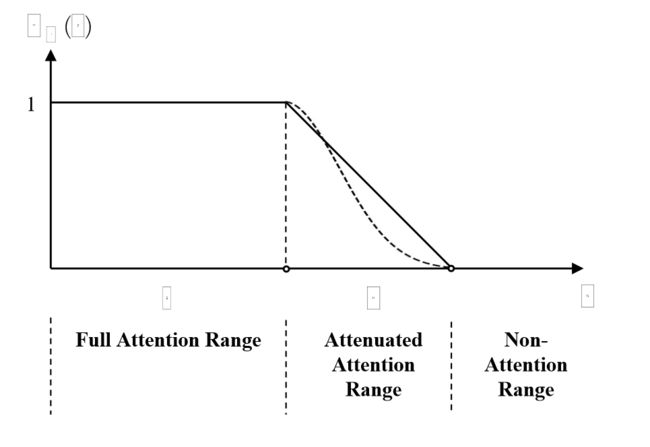
虚线表示$g_a$函数的备选项，例如：
$$\begin{array}{c}{g}_a^{\prime }(z)=\{\begin{array}{ll}1,& z\le l\\ 0,& z>l\end{array},\\ g_a^{\prime \prime }(z)=\{\begin{array}{ll}1,& z\le l\\ \frac{1}{\sqrt{2\pi }\cdot \frac{d}{3}}\exp \left(-\frac{(z-l{)}^2}{2{\left(\frac{d}{3}\right)}^2}\right),& z>l\end{array}\end{array}$$
实验发现线性的衰减函数表现最好。
通过调节$\delta$可以让模型学习对应任务的最优跨度长度。多头注意力可以独立学习注意力跨度长度，从而获得不同的最佳模糊跨度。模糊attention只使用了一层，因此只影响了跨度决策，对序列中的token没有任何影响。

3. Experiments

3.1 Setup

实验在NER、RE和ASTE三个任务上的四个数据集展开。指标选择上，NER实验采用F1-score，RE采用关系严格F1-score，ASTE采用情感三元组F1-score。
模型基于BERT-base和BERT-large，在FSUIE中，向模型中加入FSA层和跨度边界预测层。其它超参数设置见原文。

3.2 Results on NER tasks

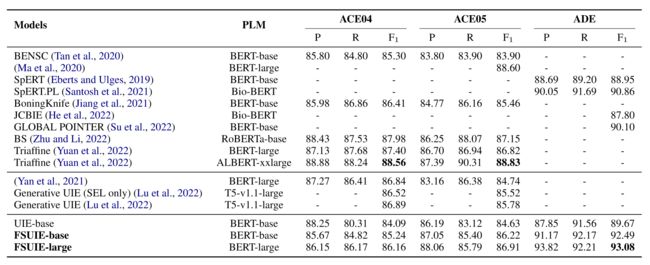
上图是NER实验的结果，可以看到与其他基于BERT架构的模型相比，FSUIE表现出不错的性能，并且在ADE数据集上有着最显著的提升，这是因为ADE数据集规模较小，更好学习到广义的模糊跨度感知表示。此外，FSUIE模型性能优于一些更大的模型，如T5模型。

3.3 Results on RE tasks

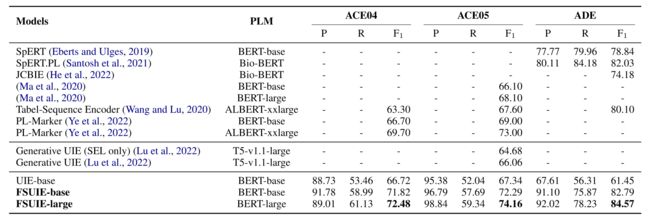
与基线UIE-base相比，FSUIE-base取得了显著的改进，尽管采用了更简单的结构和更小的主干，也能和一些更大的模型比较取得更有竞争的结果。
与一些基于跨度的抽取模型（如Bio-BERT）相比，FSUIE表现更好，说明引入的模糊跨度机制可以从数据中提取通用信息，赋予模型更强的信息抽取能力。
与生成式UIE模型相比，FSUIE不需要额外的序列生成结构，可以用更少的参数获得更高的结果。

3.4 Results on ASTE tasks

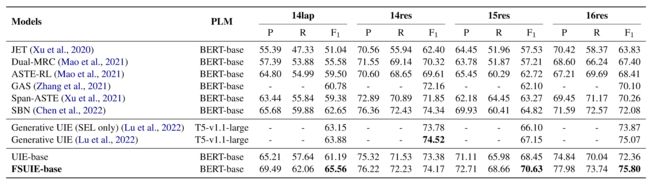
由于ASTE数据集较小，因此仅用FSUIE-base进行比较。通过引入模糊跨度机制，FSUIE模型与基线UIE-base相比显著提高了ASTE性能，在三个数据集上实现了最先进的结果。
UIE模型与其它模型之间的性能差距可以部分归因于UIE预训练的优势，并且与一些模型将一些任务分解为多个子任务相比，FSUIE模型使用统一的模型架构实现了更好的性能。
在ASTE任务上，基于跨度的UIE模型与基于生成的UIE模型相反，可以利用预测跨度的完整语义信息来协助提取观点和情感。此外，FSUIE是对抽取任务真实结构的反应，避免了生成结构带来的额外参数。

3.5 Results on Low-resource Settings

为了证明模型的鲁棒性，在低资源场景进行了实验，结果如下：

根据上表结果，进一步证明了FSUIE在低资源场景相对于UIE的优越性。

3.6 Ablation Study

本小节进行消融实验，测试UIE-base、UIE-base+FSL、UIE-base+FSA以及FSUIE在NER数据集ACE04上的表现，结果如下图所示：

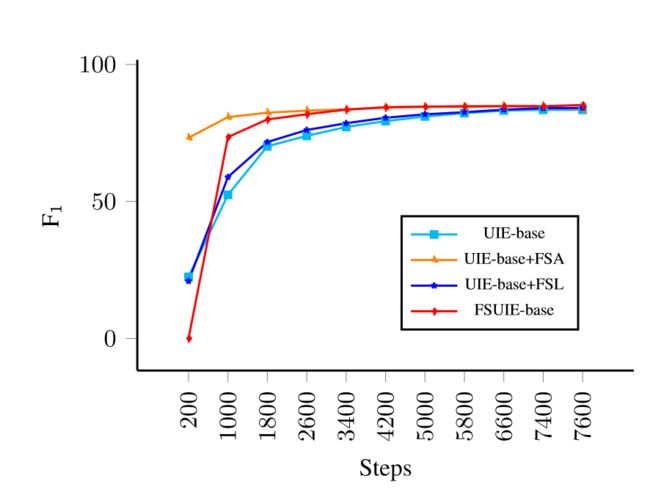
可以看到模型在FSA下能够更快收敛，对于FSA来说，模型将注意力集中在必要的位置上，并更好捕获序列跨度，而FSL对收敛速度并没有多大的提升。
为了进一步研究FSL和FSA对模型性能提升的贡献，使用了ADE数据集对NER任务进行消融实验。

可以发现，引入FSL可以提高模型性能，引入FSA模型性能略有下降。这是因为单独引入FSA让模型只关注特定部分，导致部分信息丢失。FSL的引入缓解了模型对标签跨度边界的依赖，允许模型提取更多信息，FSA引导模型从更丰富的信息中过滤出关键的信息，从而获得实质性改进。

3.7 Visualization of FSA

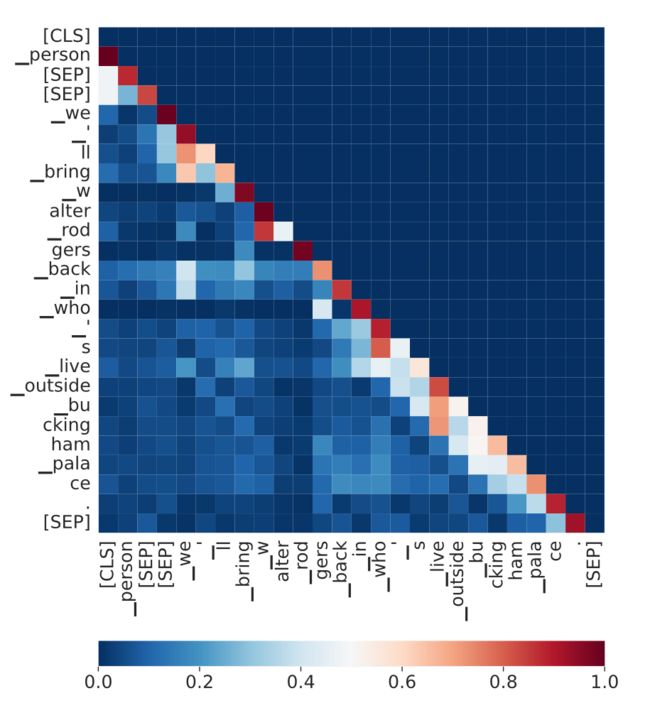
为了进一步检验模糊跨度机制的有效性，可视化了FSA层的注意力分布，可以发现最终编码序列中每个token倾向于关注先前标记的有限范围内的语义信息。

4. Related Work

略

5. Conclusion

本文提出FSUIE框架，可以提高通用信息抽取能力，具体来说，提出了模糊跨度损失和模糊注意力，实验证明了模型的性能，以及在低资源场景下的泛化性和快速收敛性。

6. Limitations

本文框架需要更复杂的注意力机制和额外的算力，此外探索的概率密度函数有限。

阅读总结

本文提出了一个很新颖的框架，针对特定的通用抽取任务，在损失函数上和模型结构上做文章，以让通用的Transformer架构的模型能够更好应用在特定领域任务上，文章的实验部分也很具有故事性，在消融实验部分，FSL提高模型性能，FSA虽加快了收敛速度但是降低了模型性能，但是二者结合却能有更大的提升。FSL允许模型提取更多信息，FSA引导模型从更丰富的信息中过滤出关键的信息这样的解释颇具说服力，也很好用实验进行了验证。但是文章还是存在一些不足：

1. 实验不充分，生成模型只和T5进行比较，而没有和ChatGPT、BART这样的大语言生成模型比较，无法从实验角度说明跨度检测模型在抽取上比生成模型要好。
2. 概率密度函数部分缺少理论的证明，选择高斯分布过于直接，缺乏说服力。
3. 低资源场景的性能证明没有和别的模型进行对比，无法说明其更好的泛化性能。

读完这篇文章其实对我也是有一定的启发，其实现在的通用信息抽取模型用的都是大语言模型，通过指令微调来达到信息抽取的目的，如果把本文提出的理念应用到大模型上，说不定真能进一步提高模型的性能，毕竟大模型本身就是通用大模型，在数据上可以通过指令微调让其能够更好做特定领域任务，那么在模型上，在算法上，就可以从attention机制和损失函数入手，让其做特定领域任务，说不定是个很好的idea。