数据结构与算法基础(青岛大学-王卓)(6)
啊呀呀,不小心又断更快一个月了,我还是认真每天学习滴,最近还是香瓜,菜瓜,西瓜,羊角蜜不能停口啊,哈哈,二叉树这一章真是硬茬,难啃啊。
文章目录
-
- @[toc]
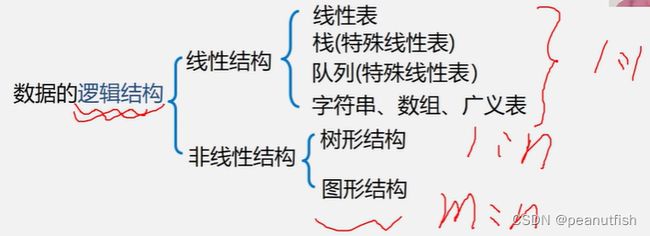
- 树和二叉树
-
- 树的定义
- 二叉树的定义
- 二叉树的性质
-
- 性质1
- 性质2
- 性质3
- 满二叉树
- 完全二叉树(complete binary tree)
- 性质4
- 性质5
- 二叉树的存储
-
- 顺序存储
- 二叉树链式存储
-
- 二叉链表
- 三叉链表
- 遍历二叉树
-
- 遍历方法
- 根据遍历序列确定二叉树
- 遍历的算法实现
-
- 先序遍历
- 中序遍历
- 后序遍历
- 遍历算法分析
- 中序遍历二叉树非递归算法
- 二叉树的层次遍历
- 二叉树遍历算法的应用
-
- 二叉树的建立
- 复制二叉树
- 计算二叉树深度
- 计算二叉树结点总数
- 计算二叉树叶子结点个数
- 线索二叉树
- 树和森林
-
- 定义
- 树的存储结构
-
- 双亲表示法
- 孩子链表
- 孩子兄弟表示法(二叉链表表示法)
- 树和二叉树的转换
-
- 将树转换为二叉树
- 将二叉树转化为树
- 森林和二叉树的转换
-
- 森林转二叉树(二叉树与多棵树之间的关系)
- 二叉树转森林
- 树的遍历
- 哈夫曼树
-
- 基本概念
- 哈夫曼算法过程(构造哈夫曼树的方法)
- 哈夫曼算法存储
- 哈夫曼算法实现
- 哈夫曼编码
-
- 什么是哈夫曼编码
- 哈夫曼编码算法
- 应用举例
文章目录
-
- @[toc]
- 树和二叉树
-
- 树的定义
- 二叉树的定义
- 二叉树的性质
-
- 性质1
- 性质2
- 性质3
- 满二叉树
- 完全二叉树(complete binary tree)
- 性质4
- 性质5
- 二叉树的存储
-
- 顺序存储
- 二叉树链式存储
-
- 二叉链表
- 三叉链表
- 遍历二叉树
-
- 遍历方法
- 根据遍历序列确定二叉树
- 遍历的算法实现
-
- 先序遍历
- 中序遍历
- 后序遍历
- 遍历算法分析
- 中序遍历二叉树非递归算法
- 二叉树的层次遍历
- 二叉树遍历算法的应用
-
- 二叉树的建立
- 复制二叉树
- 计算二叉树深度
- 计算二叉树结点总数
- 计算二叉树叶子结点个数
- 线索二叉树
- 树和森林
-
- 定义
- 树的存储结构
-
- 双亲表示法
- 孩子链表
- 孩子兄弟表示法(二叉链表表示法)
- 树和二叉树的转换
-
- 将树转换为二叉树
- 将二叉树转化为树
- 森林和二叉树的转换
-
- 森林转二叉树(二叉树与多棵树之间的关系)
- 二叉树转森林
- 树的遍历
- 哈夫曼树
-
- 基本概念
- 哈夫曼算法过程(构造哈夫曼树的方法)
- 哈夫曼算法存储
- 哈夫曼算法实现
- 哈夫曼编码
-
- 什么是哈夫曼编码
- 哈夫曼编码算法
- 应用举例
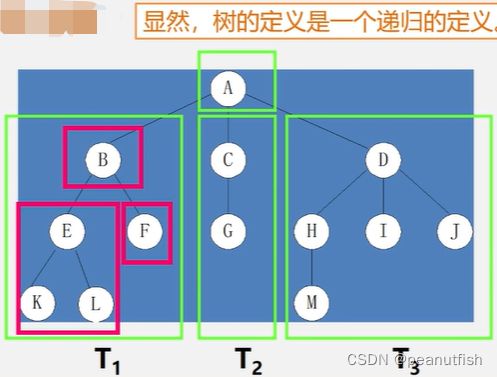
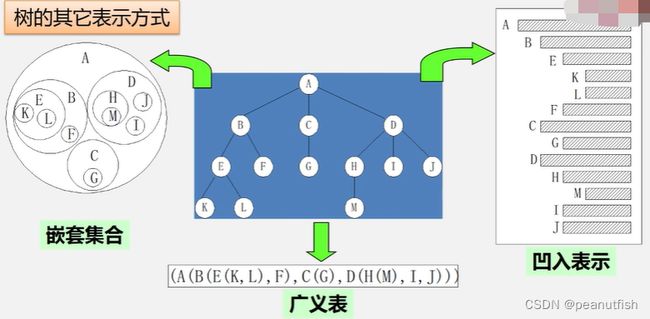
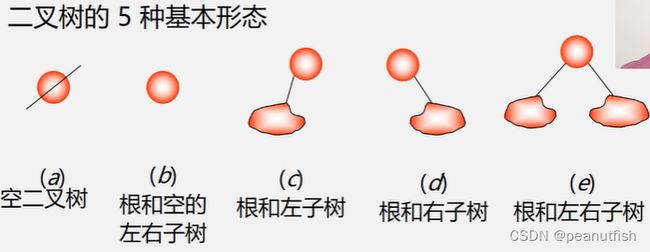
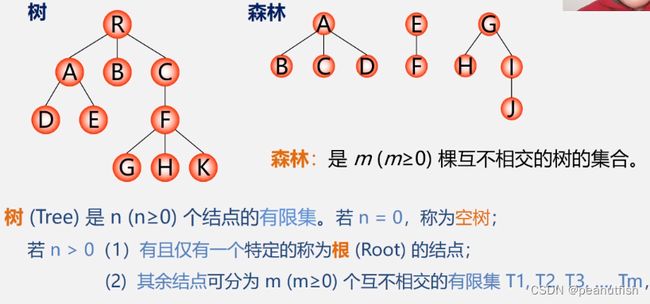
树和二叉树
树的定义
-
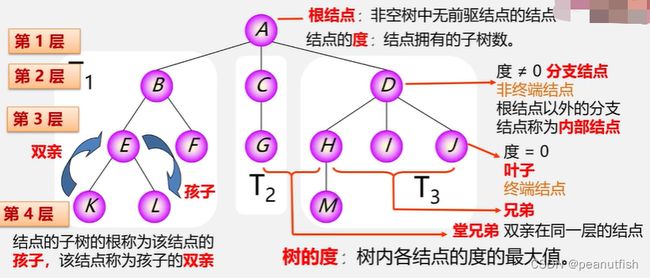
树的深度:树中节点的最大层次
-
有序树 : 树中结点的各子树从左至右有次序 ( 最左边的为第一个孩子 )
-
无序树 : 树中结点的各子树无次序 。
-
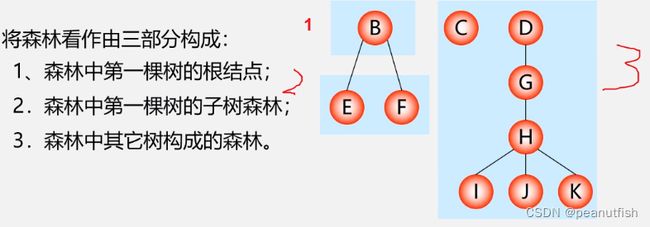
森林 : 是 m (m>=0) 棵互不相交的树的集合, 把根节点删除就变成了森林,一棵树可以看成是一个特殊的森林,给森林中的各子树加上一个双亲结点 , 森林就变成了树 。
-
树一定是森林,但是森林不一定是树。
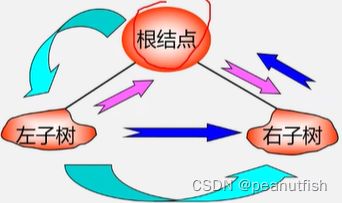
二叉树的定义
二叉树是n( n>=0 )个结点的有限集 , 它或者是空集 (n=0),
或者由一个根结点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成 。
特点:
-
每个结点最多有俩孩子 ( 二叉树中不存在度大于 2 的结点)
-
子树有左右之分,其次序不能颠倒
-
二叉树可以是空集合 ,根可以有空的左子树或空右子树 。
二叉树的性质
性质1
在二叉树的第i层上至多有2i-1个节点(i>=1),至少有1个结点

性质2
深度为k的二叉树至多有2k-1个节点(k>=1), 至少有k个结点(单支树)

性质3
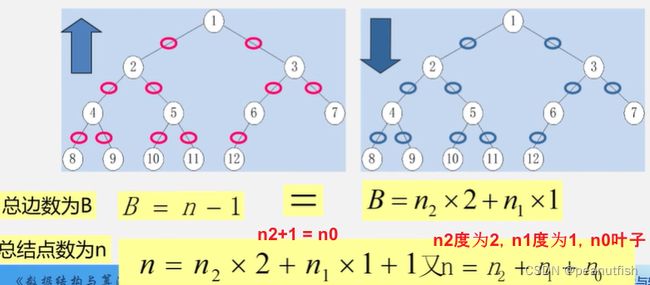
对任何一颗二叉树T,如果其叶子数为n0,度为2的结点数为n2,则n0=n2+1
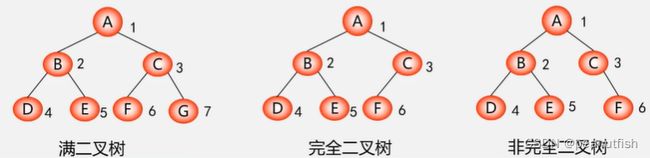
满二叉树
特点 :
- 每一层上的结点数都是最大结点数(即每层都满)
- 叶子节点全部在最底层
- 对满二叉树结点位置进行编号: 从根结点开始 , 自上而
下 , 自左而右,每一结点位置都有元素 。
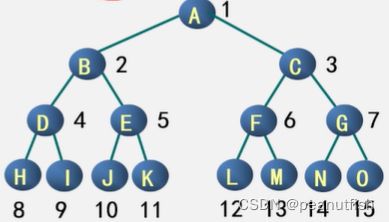
完全二叉树(complete binary tree)
定义:深度为k的具有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树。
注: 在满二叉树中 , 从最后一个结点开始 ,连续去掉任意个结点 , 即是一棵完全二叉树 .
一定是连续的去掉 ! ! !
特点:
- 叶子只可能分布在层次最大的两层上 。
- 对任一结点 , 如果其右子树的最大层次为 i,
则其左子树的最大层次必为 i 或 i + 1 。
性质4
具有n个结点的完全二叉树的深度为 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2n\rfloor + 1 ⌊log2n⌋+1
注: ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋称作x的底,表示不大于x的最大整数
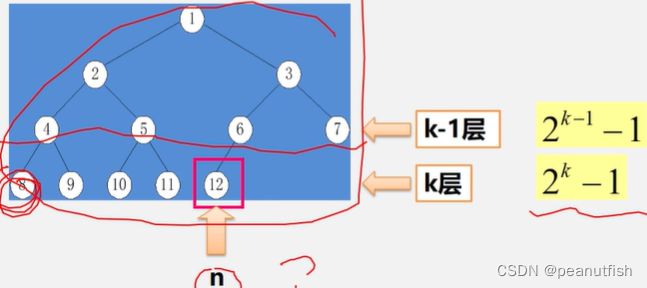
性质5
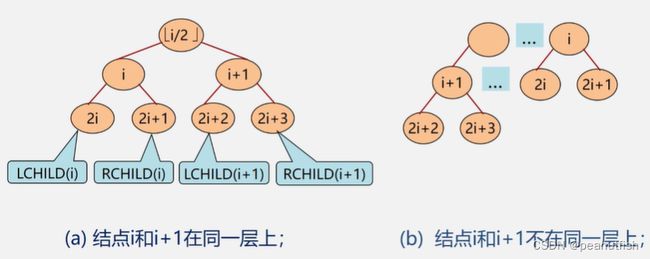
如果对一棵有n个结点的完全二叉树(深度为 ⌊ l o g 2 n ⌋ \lfloor log_2n \rfloor ⌊log2n⌋+ 1)的结点按层序编号(从第一层到 ⌊ l o g 2 n ⌋ \lfloor log_2n \rfloor ⌊log2n⌋+ 1层,每层从左到右),则对任一结点i(1 ≤ \leq ≤i ≤ \leq ≤n),有:
-
如果 i = 1, 则结点 i 是一叉树的根 , 无双亲 ; 如果 i > 1 , 则其双亲是结点 ⌊ i / 2 ⌋ \lfloor i/2 \rfloor ⌊i/2⌋
-
如果 2i > n 则结点i为叶子结点,无左孩子;否则,其左孩子是结点 2i.
-
如果 2i + 1 > n则结点 i 无右孩子;否则,其右孩 子是结点 2i + 1 。
性质5表明了完全二叉树中双亲结点编号和孩子结点编号之间的关系。
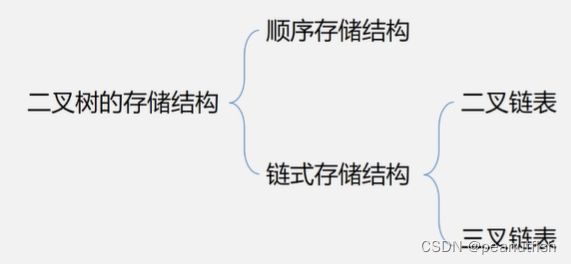
二叉树的存储
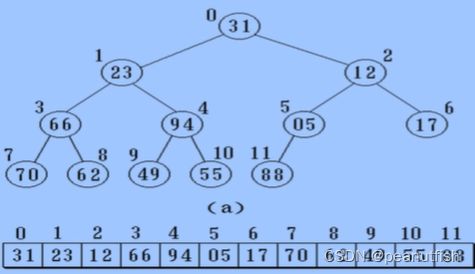
顺序存储
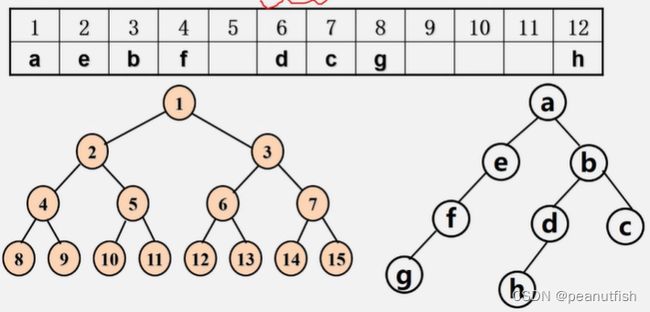
按照满二叉树的结点层次编号,依次存放二叉树中的数据元素
// 二叉树顺序存储表示
#define MAXSIZE 100
Typedef TElemType SqBiTree[MAXSIZE]
SqBiTree bt;
缺点:在右单支树情况下存储效率非常低
只适合满二叉树和完全二叉树(结点关系蕴含存储位置)
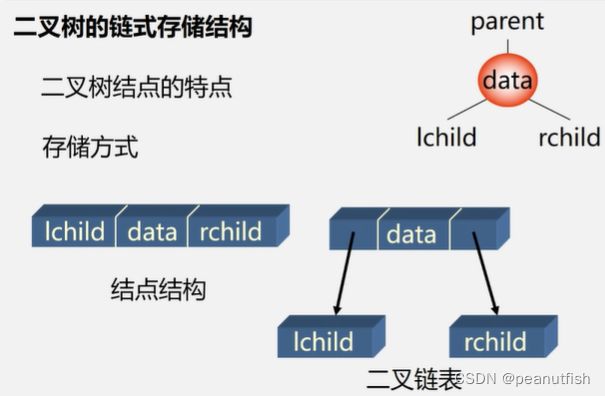
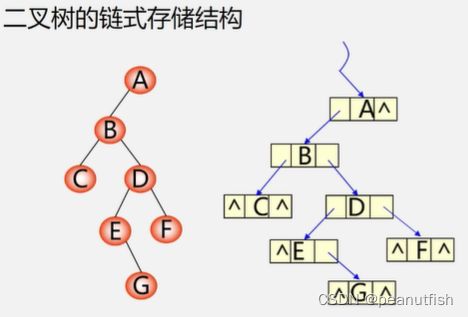
二叉树链式存储
二叉链表
// 二叉链表存储结构
typedef struct BiNode{
TElemType data;
struct BiNode *lchild,*rchild;
}BiNode, *BiTree;
在n个结点的二叉链表中,有n+1个空指针域
分析 : n个结点的二叉链表必有 2n 个链域 。 除根结点外,每个结点有且仅有一个双亲 ,所以只会有 n - 1 个结点的链域存放指针,指向非空子女结点 。
空指针数目 = 2n-(n-1)=n+1
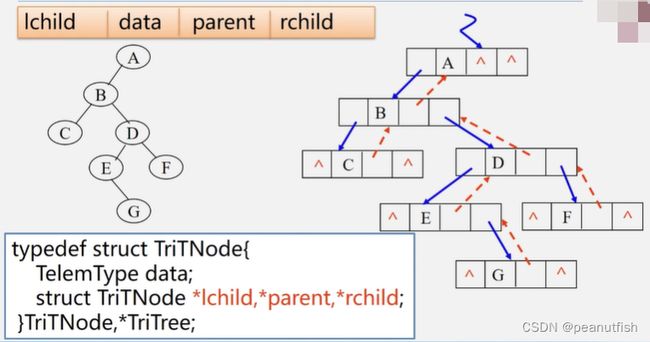
三叉链表
用于经常查找 前趋(双亲节点)
遍历二叉树
遍历是顺着某条路径巡防二叉树中的结点,每个节点都仅且访问一次,最后得到树中所有结点的一个线性排列,是树结构插删改查,排序的前提,是二叉树运算的基础和核心。
遍历方法
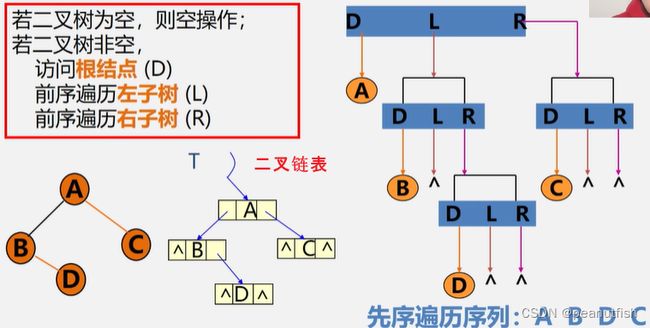
L:遍历左子树, D:访问根节点, R:遍历右子树
若规定先左后右,则有下面三种算法:(根据根被访问的顺序)
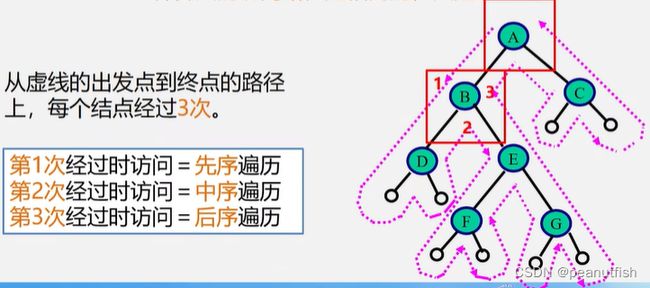
DLR - 先(根)序遍历
LDR - 中(根)序遍历
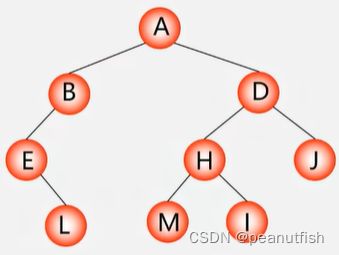
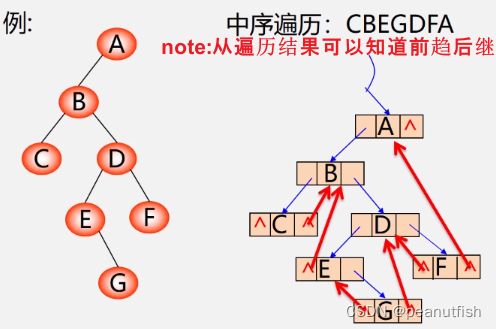
- 先序遍历 ABELDHMIJ
- 中序遍历 ELBAMHIDJ
- 后序遍历 LEBMIHJDA
小口诀:
先序有根写根,无根写左,无左写右
中序有左写左,无左写根,最后写右
后续有左写左,无左写右,最后写根
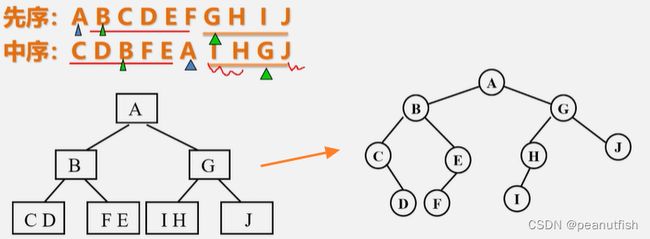
根据遍历序列确定二叉树
- 若二叉树中的各结点的值均不相同,则先序、中序,后序遍历的结果都是唯一的。
- 由二叉树的先序序列+中序序列,或者后续序列+中序序列 可以确定唯一一棵二叉树。
遍历的算法实现
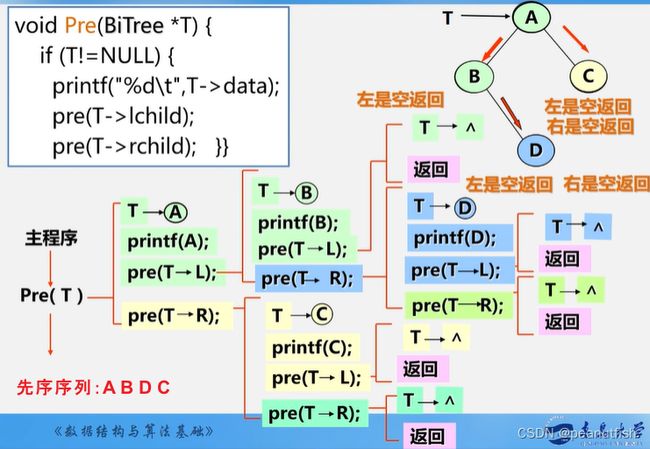
先序遍历
Status PreOrderTraverse(BiTree T){
if (T==None) return OK; //空树情况
else {
visit(T); //访问根节点
// printf("%d\t", T->data) 访问根节点数据
PreOrderTraverse(T->lchild); //递归遍历左子树
PreOrderTraverse(T->rchild); //递归遍历右子树
}
}
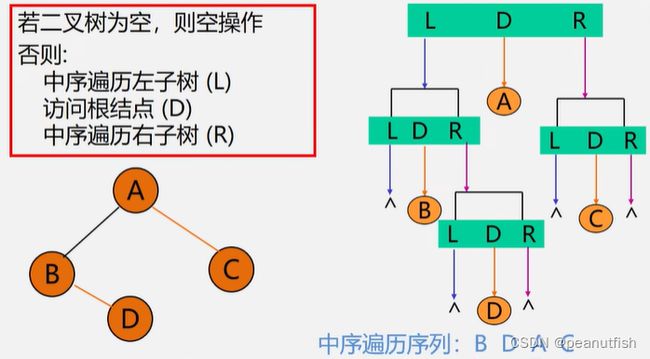
中序遍历
Stataus InOrderTraverse(BiTree T){
if (T==None) return OK; // 空二叉树
else {
InOrderTraverse(T->lchild); // 递归中序遍历左子树
visit(T); // 访问根节点
InOrderTraverse(T->rchild); // 递归中序遍历右子树
}
}
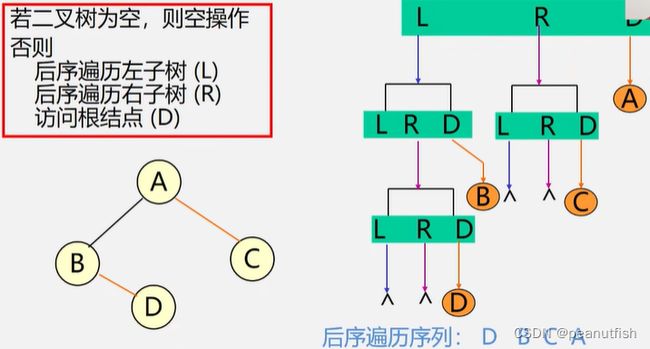
后序遍历
Stataus PostOrderTraverse(BiTree T){
if (T==None) return OK; // 空二叉树
else {
PostOrderTraverse(T->lchild); // 递归后序遍历左子树
PostOrderTraverse(T->rchild); // 递归后序遍历右子树
visit(T); // 访问根节点
}
}
遍历算法分析
如果上面三种算法去掉输出语句(visit(T)),那么从递归角度看三种算法是完全一样的,折算中算法访问路径是相同的,只是访问时机不同。
- 时间复杂度O(n), 每个结点只访问一次
- 空间复杂度O(n),栈占用的最大辅助空间
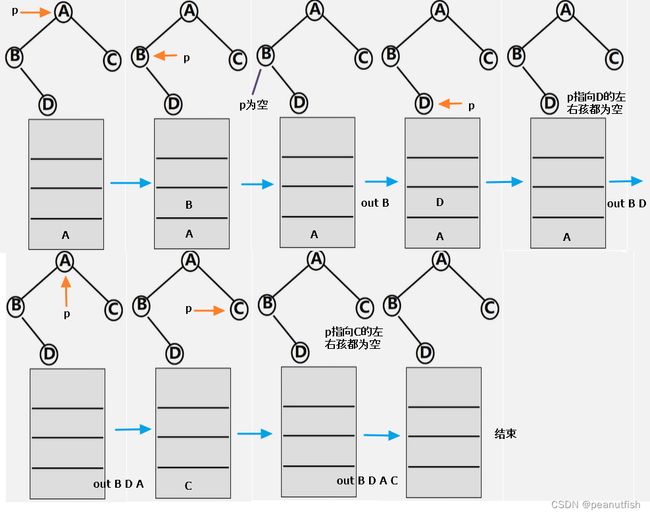
中序遍历二叉树非递归算法
中序遍历的非递归算法的关键:在中序遍历过某结点的整个左子树后,如何找到该结点的根以及右子树。
基本思想:
- 建立一个栈
- 根结点进栈,遍历左子树
- 根结点出栈,输出根结点,遍历右子树
// 中序遍历非递归算法
Status InOrderTraverse(BiTree T){
BiTree *p; // 初始化一个指针p
InitStack(S); // 初始化一个栈
p=T; // 初始是p指向二叉树根节点
if (T==None) return OK; // 空二叉树情况
else {
while (p || !StackEmpty(S)) { //指针p或者栈不为空时
if (p) { // 当p指向根节点
Push(S,p); // 入栈根节点
p=p->lchild; // p指向根的左孩子
}
else { // 当指针p为空,栈不为空时
Pop(S,q); // 弹出栈顶元素
printf("%c\t", q->data); // 输出根节点数据
p=q->rchild; // 指针p指向右孩子
}
}
return OK;
}
}
二叉树的层次遍历
对于一颗二叉树,从根结点开始,按从上到下、从左到右的顺序访问每一个结点 。每一个结点仅仅访问一次。

算法设计思路:使用一个队列
-
将根结点进队
-
队不空时循环:从队列中出列一个结点 *p,访问它;
a. 若它有左孩子结点,将左孩子结点进队,
b. 若它有右孩子结点,将右孩子结点进队。
定义顺序循环队列:
typedef struct SqQueue {
BTNode data[MAXSIZE]; // 存放对中元素
int front, rear; // 队头和队尾指针
}//SqQueue // 顺序循环队列类型
算法实现
void LevelOrder(BTNode *b) {
BTNode *p; SqQueue *qu; // 创建临时指针p和queue的指针qu
InitQueue(qu); // 初始化循环队列
enQueue(qu,b); // 将指向根节点的b元素入队
while (!QueueEmpty(qu)) { // 队列不空时
deQueue(qu, p); // 将队首元素出队并赋值给p
printf("%c", p->data)
if (p->lchild!=None) {enQueue(qu,p->lchild)}; // 有左孩子时将其入队
if (p->rchild!=None) {enQueue(qu,p->rchild)}; // 有右孩子时将其入队
}
}
二叉树遍历算法的应用
二叉树的建立
按先序遍历建立二叉树的二叉链表
- 从键盘输入二叉树结点信息,建立二叉树的存储结构
- 在建立过程中按照二叉树先序方法建立(DLR)
// 由先序序列创建二叉树
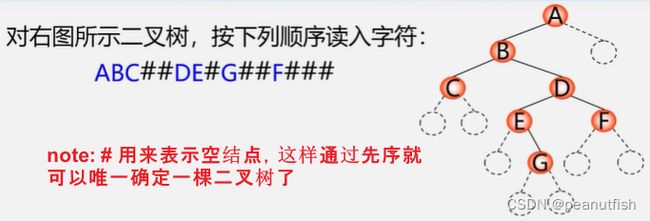
// 先序序列 例子:ABC##DE#G##F###
Status CreateBiTree(BiTree &T){
scanf(&ch); //cin>>ch(C++)
if (ch == '#') T == NULL;
else {
if (!(T=(BiTNode *)malloc(sizeof(BiTNode)))) exit(OVERFLOW); // T=new BiTNode(C++) 分配空间给根结点
T->data=ch; // 根结点赋值
CreateBiTree(T->lchild); // 构造左子树
CreateBiTree(T->rchild); // 构造右子树
}
return OK;
}
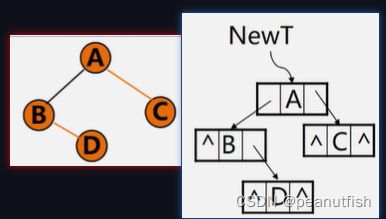
复制二叉树
思想:
- 如果是空树,递归结束,
- 否则,申请新结点空间,复制根结点
- 递归复制左子树
- 递归复制右子树
// 通过先序遍历的顺序复制一个二叉树
int Copy(BiTree T, BiTree &NewT){
if (T==NULL) { // 空树则返回0
NewT=NULL;
return 0
}
else {
NewT=new BiTNode; // 分配空间给NewT
NewT->data = T->data; // 根结点复制
Copy(T->lchild, NewT->lchild); // 左子树复制
Copy(T->rchild, NewT->rchild); // 右子树复制
}
}
计算二叉树深度
如果是空树,则深度为0,否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n, 二叉树的深度则为m与n的较大者加1。
// 计算二叉树的深度
int Depth(BiTree T){
if (T==NULL) return 0; // 空树情况
else {
m = Depth(T->lchild);
n = Depth(T->rchild);
if (m > n) return (m+1);
else return (n+1);
}
}
计算二叉树结点总数
如果是空树,则结点个数为0,否则,结点个数为左子树的结点个数 + 右子树的结点个数再 + 1
// 计算二叉树结点总数
int NodeCount(BiTree T){
if (T==NULL) return 0;
else {
return NodeCount(T->lchild) + NodeCount(T->rchild) + 1;
}
}
计算二叉树叶子结点个数
如果是空树,则叶子结点个数为 0 ,否则,为左子树的叶子结点个数 + 右子树的叶子结点个数
// 计算二叉树叶子结点个数
int LeafCount(BiTree T){
if (T==NULL) return 0; // 空树情况
if (T->lchild==NULL & T->rchild=NULL) return 1; // 无孩子的结点为叶子结点
else {
return LeafCount(T->lchild) + LeafCount(T->rchild);
}
}
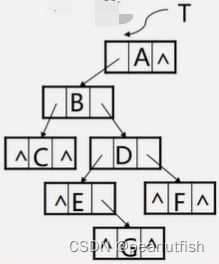
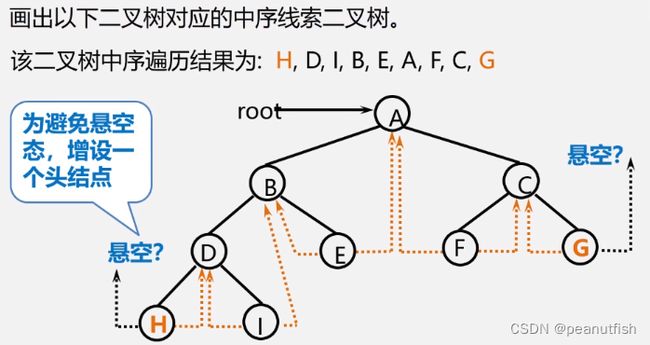
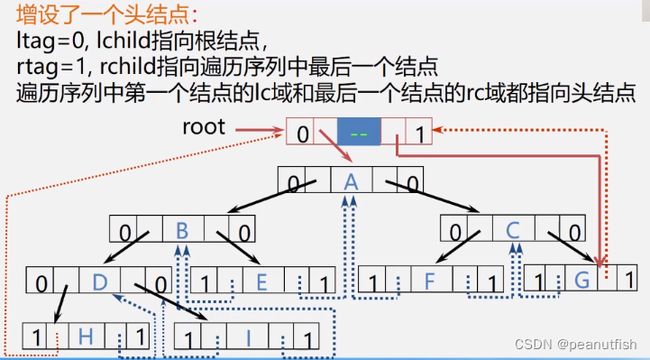
线索二叉树
利用二叉链表中的空指针域(无左/右孩子):
-
如果某个结点的左孩子为空,则将空的左孩子指针域改为指向其前驱,如果某结点的右孩子为空,则将空的右孩子指针域改为指向其后继这种改变指向的指针称为"线索".
-
加上了线索的二叉树称为线索二叉树 (Threaded Binary Tree)
-
对二叉树按某种遍历次序使其变为线索二叉树的过程叫线索化
为了区分lrchild和rchild指针到底指向孩子还是指向前趋后继的指针,对二叉链表每个结点新增两个标志域ltag,rtag,并约定:
结点结构:
![]()
typedef struct BiThrNode{
int data;
int ltag,rtag;
struct BiThrNode *lchild, *rchild;
} BiThrNode, *BiThrTree;
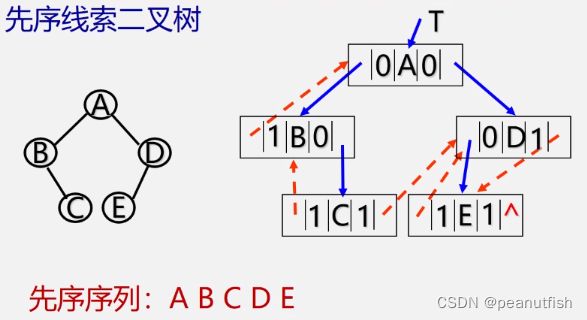
先序线索二叉树:
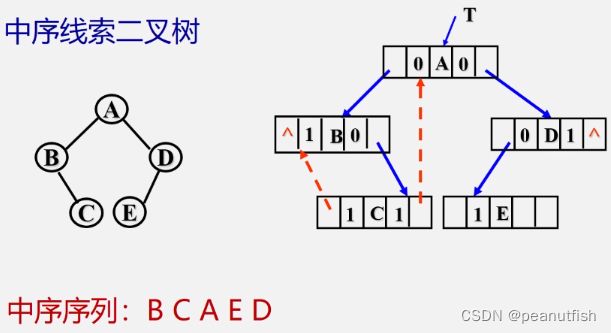
中序线索二叉树:
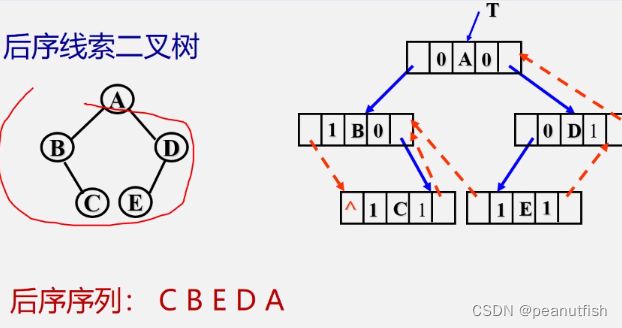
后序线索二叉树:
树和森林
定义
树的存储结构
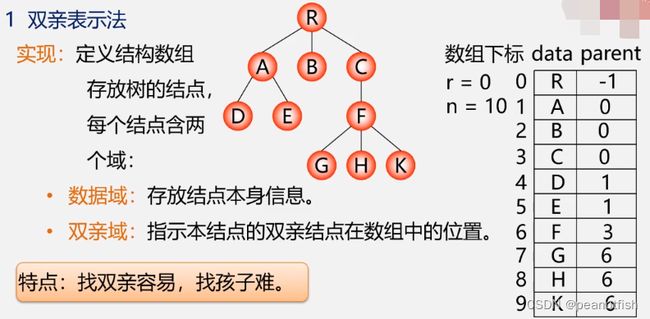
双亲表示法
特点:找双亲容易,找孩子难
C的类型描述:
-
结点结构:
typedef struct PTNode { TElemType data; int parent; // 双亲位置域 }PTNode; -
树结构:
# define MAX_TREE_SIZE 100 typedef struct { PTNode nodes[MAX_TREE_SIZE]; int r,n; // 根结点的位置和结点个数 }PTree;
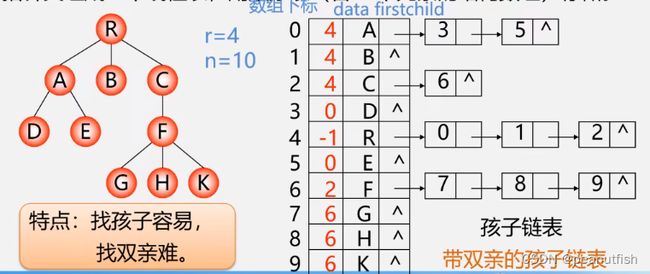
孩子链表
特点:找孩子容易,找双亲难
把每个结点的孩子结点排列起来,看成是一个线性表,用单链表存储,则n个结点有n个孩子链表(叶子的孩子链表为空表)。而n个头
指针又组成一个线性表,用顺序表(含n个元素的结构数组)存储。
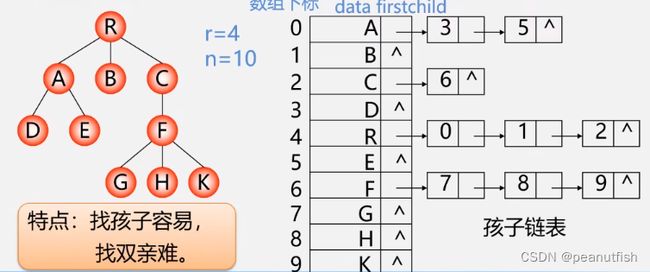
进化一下,加上双亲位置,变成带双亲的孩子链表
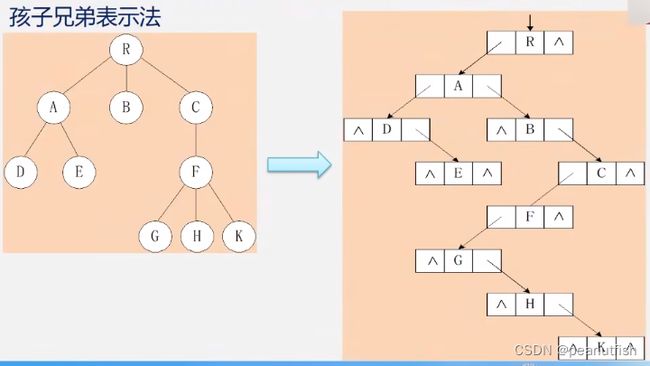
孩子兄弟表示法(二叉链表表示法)
实现 : 用二叉链表作树的存储结构,链表中每个结点的两个指针域分别指向其第一个孩子结点和下一个兄弟结点。
缺点:不好找双亲
typedef struct CSNode {
ElemType data;
struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;
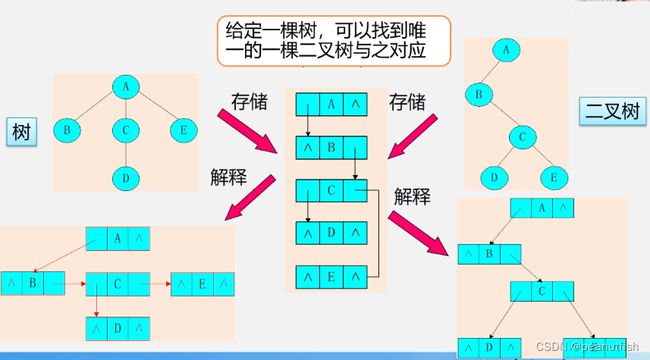
树和二叉树的转换
由于树和二叉树都可以用二叉链表作存储结构,则以二叉链表作媒介可以导出树与二叉树之间的一个对应关系。
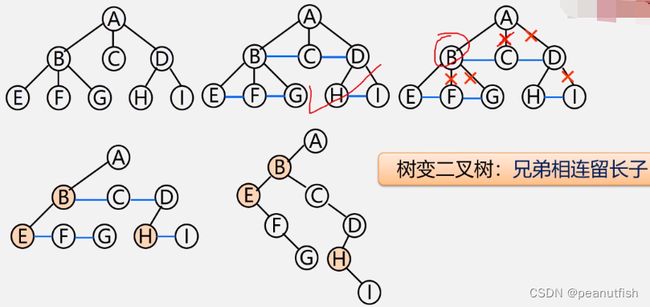
将树转换为二叉树
1. 加线:在兄弟之间加一连线
2. 抹线:对每个结点,除了其左孩子外,去除其根节点与其余孩子之间的关系
3. 旋转:以树的根结点为轴心,将整树顺时针转45度
==>树变二叉树:兄弟相连留长子
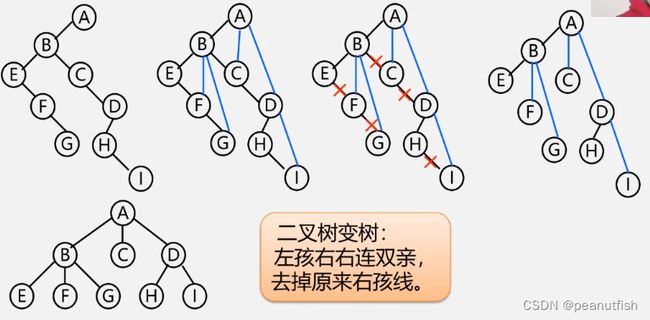
将二叉树转化为树
1. 加线:若p结点是双亲结点的左孩子,则将p的右孩子,右孩子
的右孩子。。。沿分支找到的所有右孩子,都与p的双亲用线连起来
2. 抹线:抹掉原二叉树中双亲与右孩子之间的连线.
3. 调整:将结点按层次排列,形成树结构
==>二叉树变树:左孩右右连双亲,去掉原来右孩线
森林和二叉树的转换
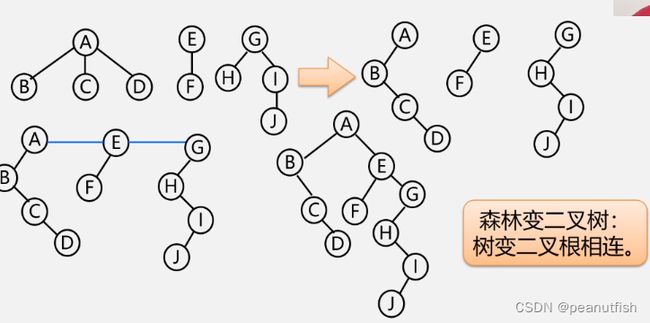
森林转二叉树(二叉树与多棵树之间的关系)
- 将各棵树分别换成二叉树
- 将每棵树的根结点用线相连
- 以第一棵树根结点为二叉树的根,再以根结点为轴心,顺时针旋转,构成二叉树型结构
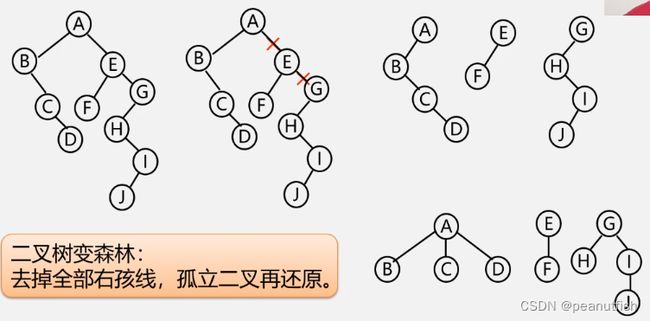
二叉树转森林
- 抹线:将二叉树中根结点与其右孩子连线,及沿右分支搜索到的所有右孩子间连线全部抹掉,使之变成孤立的二叉树
- 还原:将孤立的二叉树还原成树
树的遍历
-
三种遍历方式:
-
森林的遍历
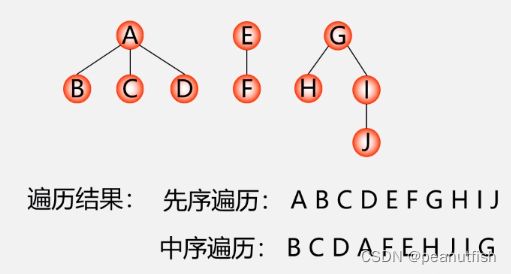
对森林的先序遍历可以看成依次对每棵子树的先序遍历然后拼在一起;
对森林的中序遍历可以看成依次对每棵子树的后序遍历然后拼在一起。
哈夫曼树
David Albert Huffman - 哈夫曼编码闻名
基本概念
-
路径:从树中一个结点到另一个结点之间的分支构成这两个结点间的路径。
-
结点的路径长度:两结点间路径上的分支数。
-
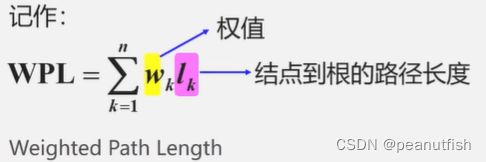
树的路径长度:从树根到每一个结点的路径长度之和。记作: TL
-
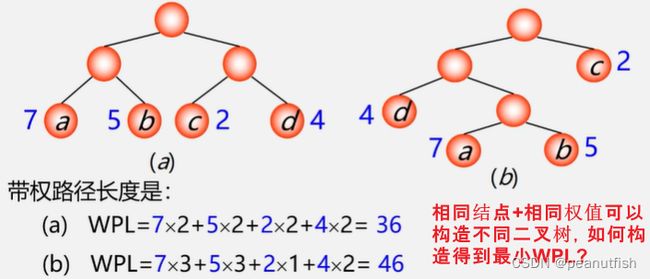
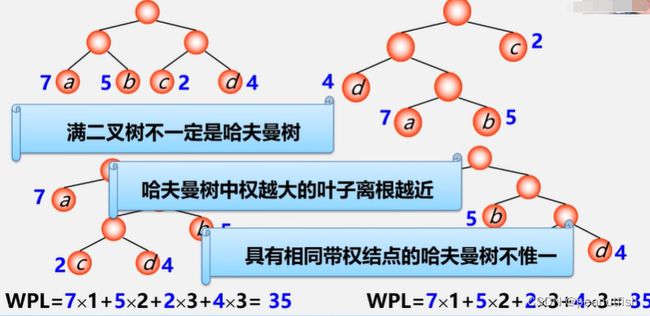
结点数目相同的二叉树中,完全二叉树是路径长度最短的二叉树。
-
权(weight):将树中结点赋给一个有着某种含义的数值(eg.占比),则这个数值称为该结点的权。
-
结点的带权路径长度:从根结点到该结点之间的路径长度与该结点的权的乘积。
-
树的带权路径长度:树中所有叶子结点的带权路径长度之和。
-
哈夫曼树:最优树 - 带权路径长度(WPL)最短的树
-
哈夫曼树:最优二叉树 - 带权路径长度(WPL)最短的二叉树
-
构造哈夫曼树算法在1952年提出,称为哈夫曼算法
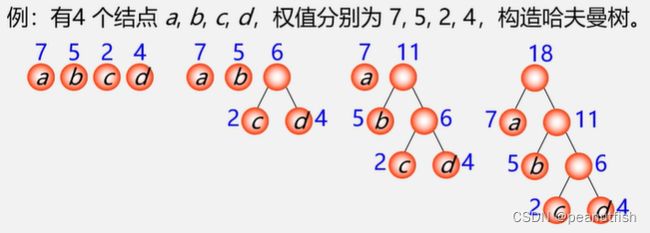
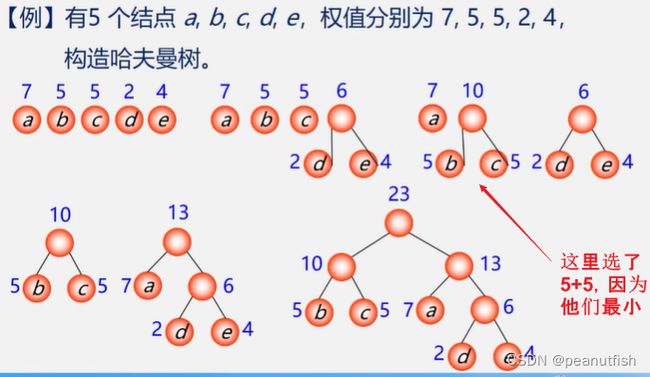
哈夫曼算法过程(构造哈夫曼树的方法)
- 根据n个给定的权值{w1,w2…,wn} 构成棵二叉树的森林 F={T1, T2, …,Tn},其中Ti只有一个带权为Wi的根结点。
- 在F中选取两棵根结点的权值最小的树作为左右子树,构造一棵新的
二叉树 ,且设置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。 - 在 F 中删除这两棵树,同时将新得到的二叉树加入森林中。
- 重复(2)和(3),直到森林中只有一棵树为止,这棵树即为哈夫曼树。
口诀:
构造森林全是根
选用两小造新树
删除两小添新人
重复2、3剩单根
-
包含 n 个叶子结点的哈夫曼树中共有 2n-1 个结点。
-
包含 n 棵树的森林要经过 n-1 次合并才能形成哈夫曼树,共产生 n-1 个新结点,且这 n-1 个新结点都是具有两个孩子的分支结点,所以总共产生 n+n-1=2n-1个结点
-
哈夫曼树的结点的度数为 0 或 2,没有度为 1 的结点。(两小造新人)
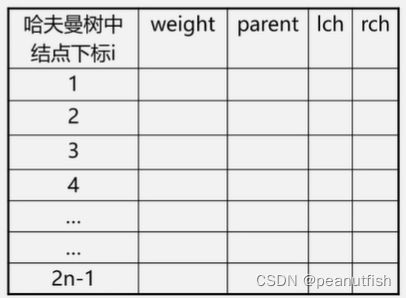
哈夫曼算法存储
-
顺序存储结构 – 一维结构数组 HuffmanTree H;
-
结点类型定义:
typedef struct { int weight; int parent, lch, rch; }HTNode, *HuffmanTree;Note: 哈夫曼树中共有 2n-1 个结点,不使用 0 下标,数组大小为2n
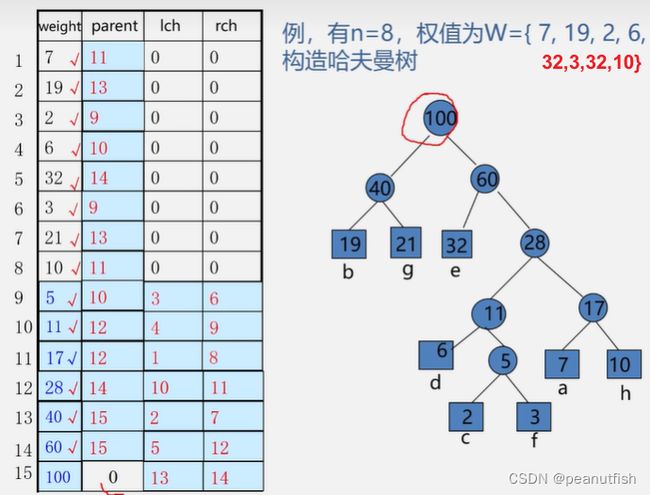
哈夫曼算法实现
-
初始化 HT[1…2n-1]:lch=rch=parent=O;
-
输入初始 n 个叶子结点:置 HT[1…n] 的 weight 值;
-
进行以下 n-1 次合并,依次产生 n-1 个结点 HT[i], i=n+1…2n-1:
- 在 HT[1…i-1] 中选两个未被选过( 从parent == 0 的结点中选 )的 weight 最小的两个结点 HT[s1]] 和 HT[s2], s1,s2为两个最小结点下标;
- 修改 HT[s1] 和 HT[s2] 的 parent 值: HT[s1].parent=i; HT[s2].parent=i;
- 修改新产生的 HT[i]:
- HT[i].weight=HT[s1].weight + HT[s2].weight
- HT[i].lch=s1; HT[i].rch=s2;
// 哈夫曼树的构造 算法5.10 void CreateHuffmanTree (HuffmanTree HT, int n) { if (n<=1) return; m=2*n-1; // 数组共2n-1个元素 HT=new HuffmanTree[m+1]; // 下标0不用,HT[m]表示根节点 for (i=1;i<=m;i++) { //初始化将所有元素的左右孩子及双亲置为0 HT[i].lch=0; HT[i].rch=0; HT[i].parent=0; } for (i=1;i<=n;i++) { // 输入前n个元素的weight值 cin>>HT[i].weight; } for (i=n+1;i<=m;i++) { // 合并产生n-1个结点 Select(HT, i-1, s1, s2); // 在HK[k](1<=k<=i-1)中选择两个其双亲域为0,且权值最小的点,并返回他们在HT中的序号s1,s2 HT[s1].parent=i; HT[s2].parent=i; // 给s1,s2加上parent,相当于从F表中删除s1,s2 HT[i].lch=s1; HT[i].rch=s2; // s1,s2设为左右孩子 HT[i].weight=HT[s1].weight+HT[s2].weight; // 新结点的权值为左右孩子之和 } }
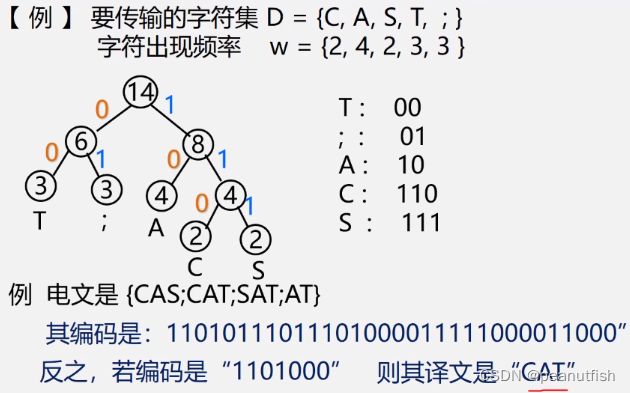
哈夫曼编码
什么是哈夫曼编码
将文字转换成0和1的电文进行发送,哈夫曼编码可以得到一种前缀码使得电文总长最短。
方法:
- 统字符集中每个字符在电文中出现的平均概率(概率越大,要求编码越短)。
- 利用哈夫曼树的特点:权越大的叶子离根越近;将每个字符的概率值作为权值,构造哈夫曼树。则概率越大的结点,路径越短。
- 在哈夫曼树的每个分支上标上 0 或 1:结点的左分支标 0 ,右分支标 1, 把从根到每个叶子的路径上的标号连接起来,作为该叶子代表的字符的编码。
自问自答:
-
为什么哈夫曼编码能够保证是前缀编码?
ANS: 因为没有一片树叶是另一片树叶的祖先,所以每个叶结点的编码就不可能是其它叶结点编码的前缀。
-
为什么哈夫曼编码能够保证字符编码总长最短 ?
ANS:因为哈夫曼树的带权路径长度最短,故字符编码的总长最短 。
性质 1 哈夫曼编码是前缀码
性质 2 哈夫曼编码是最优前缀码
哈夫曼编码算法
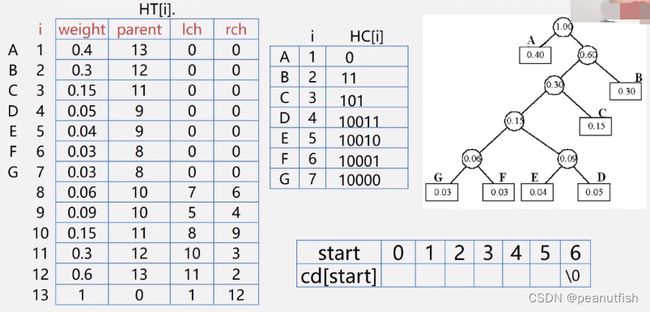
// 哈夫曼编码
void CreateHuffmanCode(HuffmanTree HT, HuffmanCode &HC, int n) {
// 从叶子到根逆向求每个字符的哈夫曼编码,存储到编码表HC中
HC = new char*[n+1]; // 分配n个字符编码的头指针矢量
cd = new char[n]; // 分配临时存放编码的动态数组空间
cd[n-1] = "\0"; // 临时表的最后一位不用设为结束符
for (i=1;i<=n;++i) { // 逐个字符求哈夫曼编码
start=n-1; c=i; f=HT[i].parent;
while (f!=0) { // 从叶子结点开始向上回溯,直到根节点
--start; // 每回溯一次 start的值向前指一个位置
if (HT[f].lch == c) cd[start]="0"; // 结点c是f的左孩子,生成代码0
else cd[start]="1"; // 结点c是f的右孩子,生成代码1
c=f; f=HT[f].parent; // 向上回溯(从parent节点继续找)
} // 求出了第i个字符的编码了
HC[i]=new char[n-start]; // 为第i个字符的编码分配空间
strcpy(HC[i], &cd[start]); // 将求得的编码从临时空间cd复制到HC当前行中
}
delete cd; // 释放临时空间
} // CreateHuffmanCode
应用举例
TO BE CONTINUED…