Dilated Convolution(空洞卷积)原理及实现

1. Dilated Convolution空洞卷积

1.1 Dilated Convolution基本原理

Dilated/Atrous Convolution(中文叫做空洞卷积或者膨胀卷积) 或者是 Convolution with holes 从字面上就很好理解，是在标准的 convolution map 里注入空洞，以此来增加 reception field。相比原来的正常convolution，dilated convolution 多了一个 hyper-parameter 称之为 dilation rate 指的是kernel的间隔数量(e.g. 正常的 convolution 是 dilatation rate 1)。

一个简单的例子，[动态图来源： https://github.com/vdumoulin/conv_arithmetic]
Standard Convolution with a 3 x 3 kernel (and padding)
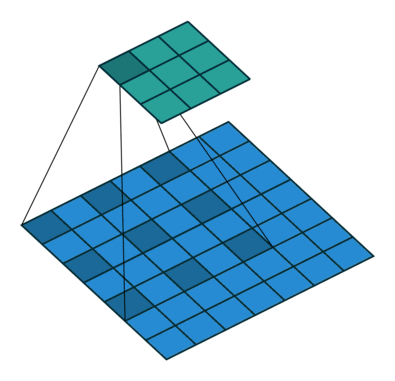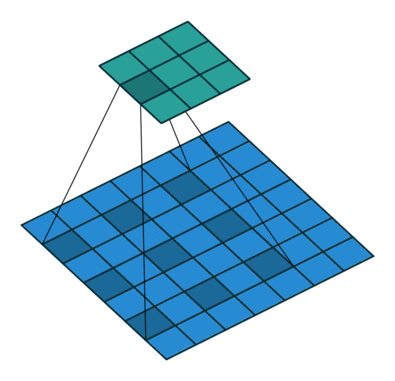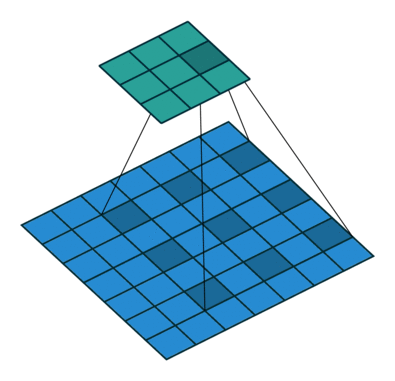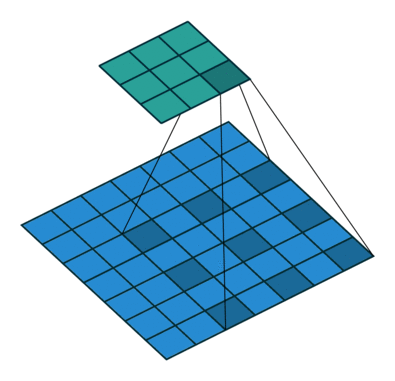Dilated Convolution with a 3 x 3 kernel and dilation rate 2

1.2 Deep CNN的缺陷

Deep CNN 对于其他任务还有一些致命性的缺陷。较为著名的是 up-sampling 和 pooling layer 的设计。主要问题有：

• Up-sampling / pooling layer (e.g. bilinear interpolation) is deterministic. (参数不可学习)
• 内部数据结构丢失；空间层级化信息丢失。
• 小物体信息无法重建 (假设有四个pooling layer 则 任何小于 2^4 = 16 pixel 的物体信息将理论上无法重建。)

在这样问题的存在下，语义分割问题一直处在瓶颈期无法再明显提高精度， 而 dilated convolution 的设计就良好的避免了这些问题。

在图像分割领域，图像输入到CNN（典型的网络比如FCN）中，FCN先像传统的CNN那样对图像做卷积再pooling，降低图像尺寸的同时增大感受野，但是由于图像分割预测是pixel-wise的输出，所以要将pooling后较小的图像尺寸upsampling到原始的图像尺寸进行预测（upsampling一般采用deconv反卷积操作，deconv可参见知乎答案 如何理解深度学习中的deconvolution networks？），之前的pooling操作使得每个pixel预测都能看到较大感受野信息。
因此, 图像分割FCN中有两个关键，一个是pooling减小图像尺寸增大感受野，另一个是upsampling扩大图像尺寸。在先减小再增大尺寸的过程中，肯定有一些信息损失掉了，那么能不能设计一种新的操作，不通过pooling也能有较大的感受野看到更多的信息呢？答案就是dilated conv。

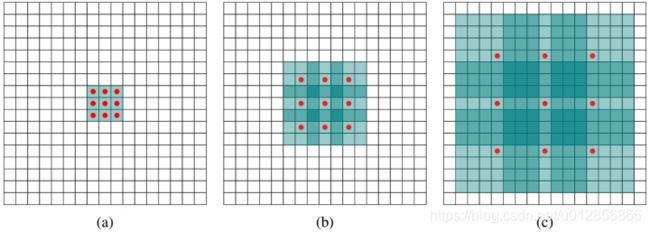
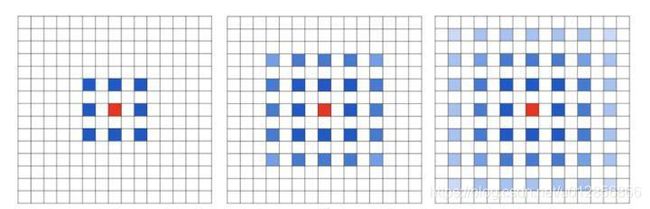
下面看一下dilated conv原始论文[4]中的示意图：

• (a)图对应3x3的1-dilated conv，和普通的卷积操作一样
• (b)图对应3x3的2-dilated conv，实际的卷积kernel size还是3x3，但是空洞为1，也就是对于一个7x7的图像patch，只有9个红色的点和3x3的kernel发生卷积操作，其余的点略过。也可以理解为kernel的size为7x7，但是只有图中的9个点的权重不为0，其余都为0。 可以看到虽然kernel size只有3x3，但是这个卷积的感受野已经增大到了7x7（如果考虑到这个2-dilated conv的前一层是一个1-dilated conv的话，那么每个红点就是1-dilated的卷积输出，所以感受野为3x3，所以1-dilated和2-dilated合起来就能达到7x7的conv）
• ©图是4-dilated conv操作，同理跟在两个1-dilated和2-dilated conv的后面，能达到15x15的感受野。对比传统的conv操作，3层3x3的卷积加起来，stride为1的话，只能达到(kernel-1)*layer+1=7的感受野，也就是和层数layer成线性关系，而dilated conv的感受野是指数级的增长。

dilated的好处是不做pooling损失信息的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。

1.3 空洞卷积存在的问题

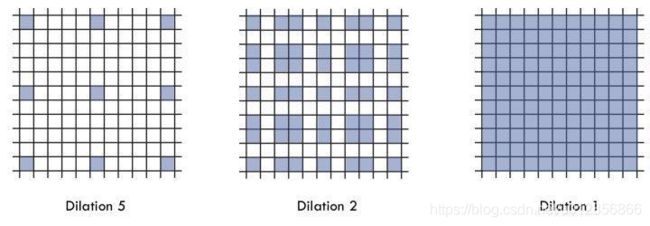
潜在问题 1：The Gridding Effect

假设我们仅仅多次叠加 dilation rate 2 的 3 x 3 kernel 的话，则会出现这个问题：

我们发现我们的 kernel 并不连续，也就是并不是所有的 pixel 都用来计算了，因此这里将信息看做 checker-board 的方式会损失信息的连续性。这对 pixel-level dense prediction 的任务来说是致命的。

潜在问题 2：Long-ranged information might be not relevant.

我们从 dilated convolution 的设计背景来看就能推测出这样的设计是用来获取 long-ranged information。然而光采用大 dilation rate 的信息或许只对一些大物体分割有效果，而对小物体来说可能则有弊无利了。如何同时处理不同大小的物体的关系，则是设计好 dilated convolution 网络的关键。

1.4 通向标准化设计：Hybrid Dilated Convolution (HDC)

对于上个 section 里提到的几个问题，图森组的文章对其提出了较好的解决的方法。他们设计了一个称之为 HDC 的设计结构。

• 第一个特性是，叠加卷积的 dilation rate 不能有大于1的公约数。比如 [2, 4, 6] 则不是一个好的三层卷积，依然会出现 gridding effect。
• 第二个特性是，我们将 dilation rate 设计成锯齿状结构，例如 [1, 2, 5, 1, 2, 5] 循环结构。
• 第三个特性是，我们需要满足一下这个式子：
  
  一个简单的例子: dilation rate [1, 2, 5] with 3 x 3 kernel (可行的方案)
  而这样的锯齿状本身的性质就比较好的来同时满足小物体大物体的分割要求(小 dilation rate 来关心近距离信息，大 dilation rate 来关心远距离信息)。

2. Dilated Convolution的tensorflow实现

2.1 tf.nn.atrous_conv2d函数解析

tf.nn.atrous_conv2d(value,filters,rate,padding,name=None）

与方法有关的一共四个主要参数：

• value：指需要做卷积的输入图像，要求是一个4维Tensor，具有[batch, height, width, channels]这样的shape，具体含义是[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数]
• filters：相当于CNN中的卷积核，要求是一个4维Tensor，具有[filter_height, filter_width, channels, out_channels]这样的shape，具体含义是[卷积核的高度，卷积核的宽度，图像通道数，卷积核个数]，同理这里第三维channels，就是参数value的第四维
• rate：要求是一个int型的正数，正常的卷积操作应该会有stride（即卷积核的滑动步长），但是空洞卷积是没有stride参数的，这一点尤其要注意。取而代之，它使用了新的rate参数，那么rate参数有什么用呢？它定义为我们在输入图像上卷积时的采样间隔，你可以理解为卷积核当中穿插了（rate-1）数量的“0”，把原来的卷积核插出了很多“洞洞”，这样做卷积时就相当于对原图像的采样间隔变大了。具体怎么插得，可以看后面更加详细的描述。此时我们很容易得出rate=1时，就没有0插入，此时这个函数就变成了普通卷积。
• padding：string类型的量，只能是”SAME”,”VALID”其中之一，这个值决定了不同边缘填充方式。

传统的tf.nn.conv2d函数中还包含有stride参数, 用于设置滑动步长的大小. 而在tf.nn.atrous_conv2d函数中已经默认了stride=1，也就是滑动步长无法改变，固定为1。

结果返回一个Tensor，填充方式为“VALID”时，返回[batch,height-2*(filter_width-1),width-2*(filter_height-1),out_channels]的Tensor，填充方式为“SAME”时，返回[batch, height, width, out_channels]的Tensor。

2.1 tf.nn.atrous_conv2d具体应用

首先创建一张2通道图

img = tf.constant(value=[[[[1],[2],[3],[4]],[[1],[2],[3],[4]],[[1],[2],[3],[4]],[[1],[2],[3],[4]]]],dtype=tf.float32)
img = tf.concat(values=[img,img],axis=3)

然后用一个3*3卷积核去做卷积

filter = tf.constant(value=1, shape=[3,3,2,5], dtype=tf.float32)
out_img = tf.nn.atrous_conv2d(value=img, filters=filter, rate=1)

建立好了img和filter，就可以做卷积了

out_img = tf.nn.conv2d(input=img, filter=filter, strides=[1,1,1,1], padding='VALID')

输出5个channel，我们设置rate=1，此时空洞卷积可以看做普通的卷积，分别在SAME和VALID模式下输出如下：

调整rate=2，继续运行程序

out_img = tf.nn.atrous_conv2d(value=img, filters=filter, rate=2, padding='SAME')

查看输出结果

[[[[ 16.  16.  16.  16.  16.]
   [ 24.  24.  24.  24.  24.]
   [ 16.  16.  16.  16.  16.]
   [ 24.  24.  24.  24.  24.]]

  [[ 16.  16.  16.  16.  16.]
   [ 24.  24.  24.  24.  24.]
   [ 16.  16.  16.  16.  16.]
   [ 24.  24.  24.  24.  24.]]

  [[ 16.  16.  16.  16.  16.]
   [ 24.  24.  24.  24.  24.]
   [ 16.  16.  16.  16.  16.]
   [ 24.  24.  24.  24.  24.]]

  [[ 16.  16.  16.  16.  16.]
   [ 24.  24.  24.  24.  24.]
   [ 16.  16.  16.  16.  16.]
   [ 24.  24.  24.  24.  24.]]]]

这个结果怎么出来的呢？再用一张图
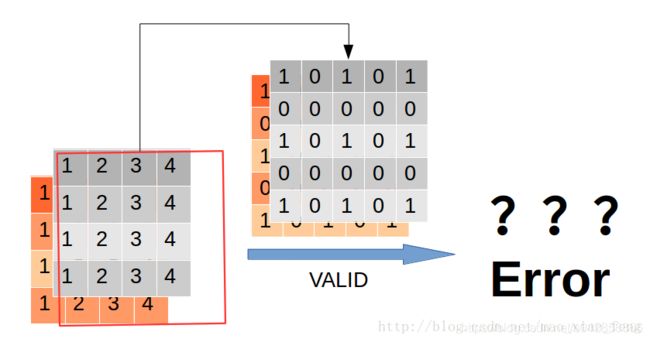
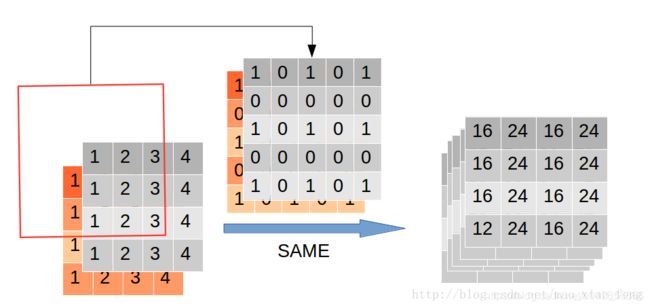这里我们看到rate=2时，通过穿插“0”，卷积核由33膨胀到了55。再看看“VALID”模式下，会发生什么？

直接报错了。因为卷积核的大小已经超过了原图大小

好了，看到这里相信大家对于空洞卷积有了基本的了解了。那么，填充方式为“VALID”时，返回[batch,height-2*(filter_width-1),width-2*(filter_height-1),out_channels]的Tensor，这个结果，相信大家就可以证明了。

完整代码如下:

import tensorflow as tf

img = tf.constant(value=[[[[1],[2],[3],[4]],[[1],[2],[3],[4]],[[1],[2],[3],[4]],[[1],[2],[3],[4]]]],dtype=tf.float32)
img = tf.concat(values=[img,img],axis=3)
filter = tf.constant(value=1, shape=[3,3,2,5], dtype=tf.float32)
out_img1 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=1, padding='SAME')
out_img2 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=1, padding='VALID')
out_img3 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=2, padding='SAME')

#error
#out_img4 = tf.nn.atrous_conv2d(value=img, filters=filter, rate=2, padding='VALID')

with tf.Session() as sess:
    print 'rate=1, SAME mode result:'
    print(sess.run(out_img1))

    print 'rate=1, VALID mode result:'
    print(sess.run(out_img2))

    print 'rate=2, SAME mode result:'
    print(sess.run(out_img3))

    # error
    #print 'rate=2, VALID mode result:'
    #print(sess.run(out_img4))

相关论文:

• Yu, Fisher, and Vladlen Koltun. “Multi-scale context aggregation by dilated convolutions.” arXiv preprint arXiv:1511.07122 (2015).
• Graph WaveNet for Deep Spatial-Temporal Graph Modeling. IJCAI 2019

参考博客:

• 空洞卷积(dilated convolution)理解
• 【Tensorflow】tf.nn.atrous_conv2d如何实现空洞卷积？