蓝桥杯 试题 算法训练 ALGO-4 结点选择 ---树形dp

资源限制
时间限制：1.0s 内存限制：256.0MB
问题描述

有一棵 n 个节点的树，树上每个节点都有一个正整数权值。如果一个点被选择了，那么在树上和它相邻的点都不能被选择。求选出的点的权值和最大是多少？
输入格式

第一行包含一个整数 n 。

接下来的一行包含 n 个正整数，第 i 个正整数代表点 i 的权值。

接下来一共 n-1 行，每行描述树上的一条边。
输出格式
输出一个整数，代表选出的点的权值和的最大值。
样例输入
5
1 2 3 4 5
1 2
1 3
2 4
2 5
样例输出
12
样例说明
选择3、4、5号点，权值和为 3+4+5 = 12 。
数据规模与约定

对于20%的数据， n <= 20。

对于50%的数据， n <= 1000。

对于100%的数据， n <= 100000。

权值均为不超过1000的正整数。

题解：
首先考虑这样一个事哈，因为树结构在处理时比较麻烦，能否根据题目的意思先简化一下，就是先让我们明白大体建立的动态规划方向，然后再考虑这个问题。题目要求树中相邻的两个节点不能同时选择，也就是说相邻的两个节点要么都不选，要么只能选择一个。
那么我们进行简化：
简化为给你一个一维数组，相邻的两个数字不能同时选择，从中选取一些数字求和，使得和最大。
这样是不是就简单多了，我们从下标1开始遍历到n，那么针对每个数字，只有两种操作：选取 or 不选取。
于是我们定义一个二维数组dp[maxn][2]
dp[i][0]表示此时不选取数字i时，1到i区间能得到的最大和
dp[i][1]表示此时选取数字i时，1到i区间能得到的最大和
于是动态规划转移方程为：

	dp[i][0]=max(dp[i-1][0],dp[i-1][1])
	/*
	说明，由题目要求可知道，当不选取数字i时，针对和数字i相邻的
	数字i-1，我们可以选取数字i-1,也可以不选取，所以返回选取和不选取时
	最大值
	*/
	dp[i][1]=dp[i-1][0]+val[i]
	/*
	这里很好理解了吧，当取数字i的时候，相邻的数字i-1不能选取，然后加上自己的权值val[i]
	*/
	//最后答案输出:
	max(dp[n][1],dp[n][0])

好了，当我们知道针对一维数组情况的动态规划转移方程时，我们大概对这个题目的动态规划方向有了大体了解，那么具体怎么结合呢？按题目给的样例做图说明（我们以1为根节点）。

我们可以发现，结合我们上述说的一维数组转移方程的情况，实际上树的每条支链，都是一个一维数组，比如1->2->4为一个一维数组，1->2->5为一个一维数组，1->3为一个一维度数组。
那么我们是不是就可以通过上述的动态转移方程，从根节点出发往子节点遍历呢?
答案是不行，因为很明显的错误是，存在分叉时，比如下图结构：

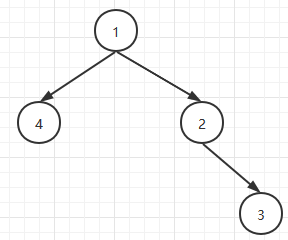
单独对两个一维数组:1->4和1->2->3进行动态规划操作，在1->4中，我们不会选取1，在1->2->3中，我们要选取1，如此就存在分歧，因为1所在节点是否选取只有一种情况。

我们的动态规划方程每个分支运算都是相互独立互不干扰的，而从根节点往下遍历，每个分支的转移都是相互干扰的，比如分支1需要选取父亲节点更好，而分支2不选取父亲节点更好。这样来就不符合我们的动态规划转移方程的要求，然后我们突然意识到，如果反过来，从叶子节点反向朝着根节点遍历，就符合了要求，因为每个子节点是否选取都是相互独立的，然后再转移到父亲节点。

而针对父亲节点的选取，利用我们的方程就可以做到：
如果父节点下标为i,子节点下标为x1,x2,…xn.
则：

dp[i][0]=max(dp[x1][0],dp[x1][1])+max(dp[x2][0],dp[x2][1])+…+max(dp[xn][0],dp[xn][1])

dp[i][1]=dp[x1][0]+dp[x2][0]+…+dp[xn][0]+val[i]

到这儿题目就解答结束了，是不是就巧妙的把一维数组的转移方程和树结构结合起来了，然后深度遍历找子节点吧。

PS：本人在算法学习过程中，主要学习图论知识，动态规划很少接触，包括比赛时也是把动态规划题目丢给队友处理，我所掌握的动态规划都是很基础的那种，比如求最长上升子序列这种入门知识，当看到这个题目的时候，我一开始想直接百度树形dp知识学习下再解决这个问题，但突然一瞬间想到树的每个支链不就相当于一个一维数组吗？而如果是一维数组的话，好像我所掌握的那点可怜的动态规划知识还是能勉强解决的，然后我又想到能否自己先考虑下一维数组的情况再想办法看看能不能和树结构结合一起，于是有了上述的整个分析过程。当时确定了一维数组的状态转移方程后，我很开心的马上和树结构结合，当发现从根节点往下遍历的时候是错误的，我一度怀疑自己的想法不能解决这个问题，于是又一直画图来找关系，最后理论上发现从子节点反过来推导就可以，然后花了几分钟把代码实现，确定样例没问题提交就直接通过了，这个研究推导过程还是挺开心的。但这是不是也说明我们学习算法或者其他东西，应该先从简单入手呢？即便这个东西很简单，因为一生万物吧，如果直接从树形dp看前人总结好的结论你不一定能有所收获，也很少能有自己推导验证的那种满足感。

最后希望我的题解分析能对你有所帮助，谢谢~

代码：

#include
using namespace std;
const int N=1e5+100;
typedef long long ll;
//dp[x][0]表示不选择这个节点，dp[x][1]表示选择该节点 
ll dp[N][2];
ll val[N];
vector<int>edge[N];
void dfs(int u,int pre)
{
	//先给所有子节点进行dp操作 
	for(int i=0;i<edge[u].size();i++)
	{
		int v=edge[u][i];
		//这棵树没有方向，要注意判别父节点和子节点 
		if(v==pre)continue;
		dfs(v,u);
	}
	for(int i=0;i<edge[u].size();i++)
	{
		int v=edge[u][i];
		if(v==pre)continue;
		//为0表示不选取u结点，那么可选择选取了子节点v和不选取子节点v两种情况
		//取最大 
		dp[u][0]+=max(dp[v][0],dp[v][1]);
	}
	for(int i=0;i<edge[u].size();i++)
	{
		int v=edge[u][i];
		if(v==pre)continue;
		//为1表示选取了u节点，那么只能选择不选取子节点v的情况 
		dp[u][1]+=dp[v][0];
	}
	dp[u][1]+=val[u];
}
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&val[i]);
		edge[i].clear();
	}
	for(int i=1;i<n;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		edge[u].push_back(v);
		edge[v].push_back(u);
	}
	memset(dp,0,sizeof(dp));
	dfs(1,-1);
	cout<<max(dp[1][0],dp[1][1])<<endl; 
	return 0;
}