python与深度学习(一):ANN和手写数字识别

1. 神经网络

神经网络是学者通过对生物神经元的研究，提出了模拟生物神经元机制的人工神经网络的数学模型，生物神经元的模型抽象为如图所示的数学结构。

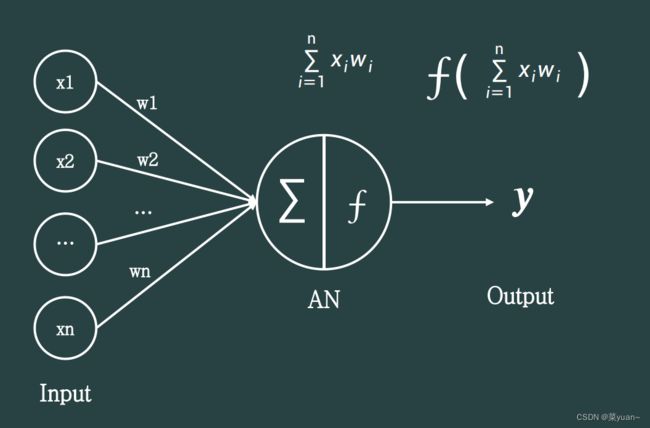
神经元输入向量 = [1,   2, 3, … , ]T，经过函数映射：: → 后得到输出。
考虑一种简化的情况，即线性变换：() = 11 + 22 + 33 + ⋯ + + b。
参数 = {1, 2, 3, . . . , , }确定了神经元的状态，通过固定参数即可确定此神经元的处理逻辑。当神经元输入节点数 = 1(单输入)时，神经元数学模型可进一步简化为： = + 。

2. 线性回归

在这里，我们通过一个线性回归的例子了解神经网络的基本思想。
线性回归问题简单来说就是找到一条曲线使得该曲线到图中各点的距离之和最短，即求出当前模型的所有采样点上的预测值() + 与真实值()之间的差的平方和作为总误差ℒ的值最小的和。

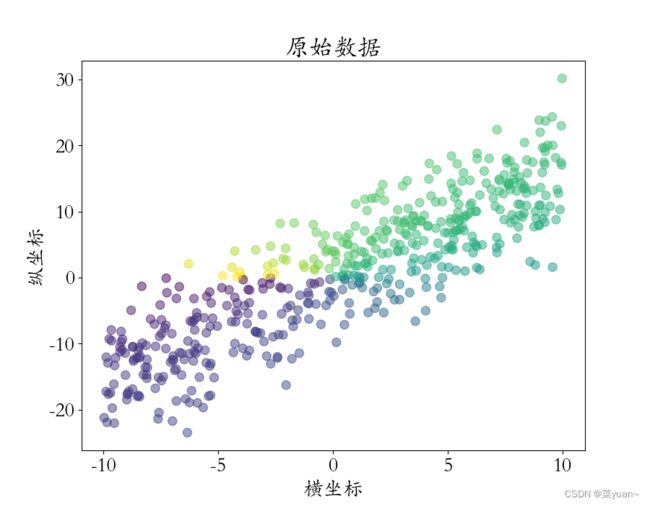
而每次寻找最优值和的过程就是训练的过程，其中寻找最优值的方法叫做优化方法，常用优化方法是梯度下降法。也就是在每次训练时让参数和按照下列式子进行更新，直到找到最优解，最终结果如下图。

其中η是学习率。

3. 激活函数

以上的例子是线性的，但是实际中有很多问题是非线性的。针对于非线性问题，可以在线性模型的基础上嵌套非线性函数，就是激活函数。

这里的代表了某个具体的非线性激活函数。

3.1 Sigmoid函数

它的一个优良特性就是能够把 ∈ 的输入“压缩”到 ∈ (0,1)区间，这个区间的数值在深度学习常用来表示以下意义：
(1) 概率分布 (0,1)区间的输出和概率的分布范围[0,1]契合，可以通过 Sigmoid 函数将输出转译为概率输出。
(2) 信号强度 一般可以将 0~1 理解为某种信号的强度，如像素的颜色强度，1 代表当前通道颜色最强，0 代表当前通道无颜色；抑或代表门控值(Gate)的强度，1 代表当前门控全部开放，0 代表门控关闭。

3.2 Relu函数

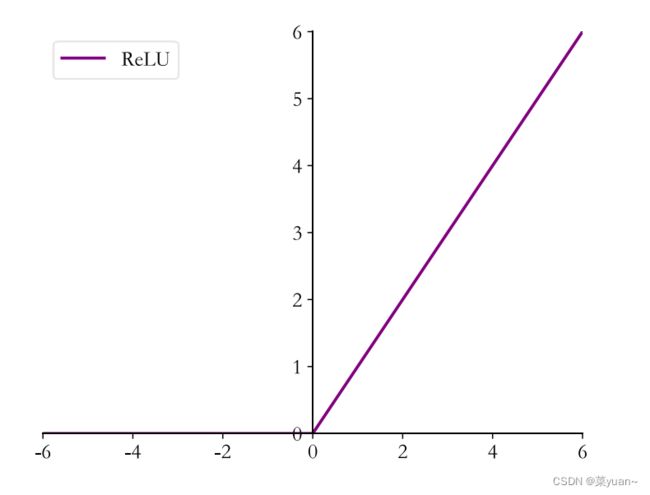
在 ReLU激活函数提出之前，Sigmoid 函数通常是神经网络的激活函数首选。但是 Sigmoid 函数在输入值较大或较小时容易出现梯度值接近于 0 的现象，称为梯度弥散现象。出现梯度弥散现象时，网络参数长时间得不到更新，导致训练不收敛或停滞不动的现象发生，较深层次的网络模型中更容易出现梯度弥散现象。因此为了解决梯度弥散问题，提出了Relu激活函数。

可以看到，ReLU 对小于 0 的值全部抑制为 0；对于正数则直接输出。

3.3 Softmax函数

Softmax 函数不仅可以将输出值映射到[0,1]区间，还满足所有的输出值之和为 1 的特性。
如图的例子，输出层的输出为[2.0,1.0,0.1]，经过 Softmax 函数计算后，得到输出为[0.7,0.2,0.1]，每个值代表了当前样本属于每个类别的概率，概率值之和为 1。通过 Softmax函数可以将输出层的输出转译为类别概率，在分类问题中使用的非常频繁。

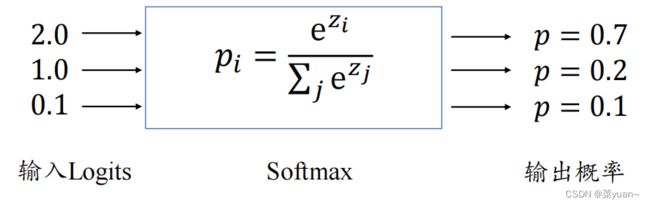
4. ANN(全连接网络)模型结构

由每个输出节点与全部的输入节点相连接，这种网络层称为全连接层。

通过层层堆叠上图中的全连接层，保证前一层的输出节点数与当前层的输入节点数匹配，即可堆叠出任意层数的网络。我们把这种由神经元相互连接而成的网络叫做神经网络。如下图所示，通过堆叠 4 个全连接层，可以获得层数为 4 的神经网络，由于每层均为全连接层，称为全连接网络。其中第 1~3 个全连接层在网络中间，称之为隐藏层 1、2、3，最后一个全连接层的输出作为网络的输出，称为输出层。隐藏层 1、2、3 的输出节点数分别为[256,128,64]，输出层的输出节点数为 10。
在设计全连接网络时，网络的结构配置等超参数可以按着经验法则自由设置。

5. 误差函数

在搭建完模型结构后，下一步就是选择合适的误差函数来计算误差。常见的误差函数有均方差、交叉熵、KL 散度、Hinge Loss 函数等，其中均方差函数和交叉熵函数在深度学习中比较常见，均方差函数主要用于回归问题，交叉熵函数主要用于分类问题。

5.1 均方差误差函数

均方差(Mean Squared Error，简称 MSE)误差函数通过计算这两个点之间的欧式距离的平方来衡量两个向量之间的差距。

MSE 误差函数的值总是大于等于 0，当 MSE 函数达到最小值 0 时，输出等于真实标签，此时神经网络的参数达到最优状态。均方差误差函数广泛应用在回归问题中，实际上，分类问题中也可以应用均方差误差函数。

5.2 交叉熵误差函数

交叉熵误差函数常用于分类问题中。

6. 手写数字识别实战

6.1 工具说明

该代码是基于TensorFlow框架书写，需要下载相关库。

6.2 导入相关库

以下第三方库是python专门用于深度学习的库

# 导入tensorflow
import tensorflow as tf
# 导入keras
from tensorflow import keras
# 引入内置手写体数据集mnist
from keras.datasets import mnist
# 引入绘制acc和loss曲线的库
import matplotlib.pyplot as plt
# 引入ANN的必要的类
from keras.layers import Dense
from keras.models import Sequential
from keras import optimizers, losses

6.3 加载数据

把MNIST数据集进行加载

"1.加载数据"
"""
x_train是mnist训练集图片,大小的28*28的,y_train是对应的标签是数字
x_test是mnist测试集图片,大小的28*28的,y_test是对应的标签是数字
"""
(x_train, y_train), (x_test, y_test) = mnist.load_data()  # 加载mnist数据集
print('mnist_data:', x_train.shape, y_train.shape, x_test.shape, y_test.shape)  # 打印训练数据和测试数据的形状

6.4 数据预处理

(1) 将输入的图片进行归一化，从0-255变换到0-1；
(2) 将输入图片的形状(60000,28,28)转换成(60000,28*28),相当于将图片拉直,便于输入给神经网络；
(3) 将标签y进行独热编码,因为神经网络的输出是10个概率值,而y是1个数， 计算loss时无法对应计算,因此将y进行独立编码成为10个数的行向量，然后进行loss的计算 独热编码:例如数值1的10分类的独热编码是[0 1 0 0 0 0 0 0 0 0,即1的位置为1，其余位置为0。

"2.数据预处理"


def preprocess(x, y):  # 数据预处理函数
    x = tf.cast(x, dtype=tf.float32) / 255.  # 将输入的图片进行归一化，从0-255变换到0-1
    x = tf.reshape(x, [28 * 28])
    """
    # 将输入图片的形状(60000,28,28)转换成(60000,28*28),
    相当于将图片拉直,便于输入给神经网络
    """
    y = tf.cast(y, dtype=tf.int32)  # 将输入图片的标签转换为int32类型
    y = tf.one_hot(y, depth=10)
    """
    # 将标签y进行独热编码,因为神经网络的输出是10个概率值,而y是1个数，
    计算loss时无法对应计算,因此将y进行独立编码成为10个数的行向量，然后进行loss的计算
    独热编码:例如数值1的10分类的独热编码是[0 1 0 0 0 0 0 0 0 0,即1的位置为1，其余位置为0
    """
    return x, y

6.5 数据处理

数据加载进入内存后，需要转换成 Dataset 对象，才能利用 TensorFlow 提供的各种便捷功能。
通过 Dataset.from_tensor_slices 可以将训练部分的数据图片 x 和标签 y 都转换成Dataset 对象

batchsz = 128  # 每次输入给神经网络的图片数
"""
数据加载进入内存后，需要转换成 Dataset 对象，才能利用 TensorFlow 提供的各种便捷功能。
通过 Dataset.from_tensor_slices 可以将训练部分的数据图片 x 和标签 y 都转换成Dataset 对象
"""
db = tf.data.Dataset.from_tensor_slices((x_train, y_train))  # 构建训练集对象
db = db.map(preprocess).shuffle(60000).batch(batchsz)  # 将数据进行预处理，随机打散和批量处理
ds_val = tf.data.Dataset.from_tensor_slices((x_test, y_test))  # 构建测试集对象
ds_val = ds_val.map(preprocess).batch(batchsz)  # 将数据进行预处理，随机打散和批量处理

6.6 构建网络模型

构建了5层ANN网络,每层的神经元个数分别是256,128,64,32,10,隐藏层的激活函数是relu,输出层的激活函数是sortmax

"3.构建网络模型"
model = Sequential([Dense(256, activation='relu'),
                      Dense(128, activation='relu'),
                      Dense(64, activation='relu'),
                      Dense(32, activation='relu'),
                      Dense(10,activation='softmax')])
"""
构建了5层ANN网络,每层的神经元个数分别是256,128,64,32,10,
隐藏层的激活函数是relu,输出层的激活函数是sortmax
"""
model.build(input_shape=(None, 28 * 28))  # 模型的输入大小
model.summary()  # 打印网络结构

6.7 模型编译

模型的优化器是Adam,学习率是0.01,
损失函数是losses.CategoricalCrossentropy,
性能指标是正确率accuracy

"4.模型编译"
model.compile(optimizer=optimizers.Adam(lr=0.01),
                loss=tf.losses.CategoricalCrossentropy(from_logits=False),
                metrics=['accuracy']
                )
"""
模型的优化器是Adam,一种优化方法，学习率是0.01,
损失函数是losses.CategoricalCrossentropy,多分类交叉熵损失函数
性能指标是正确率accuracy
"""

6.8 模型训练

模型训练的次数是5,每1次循环进行测试

"5.模型训练"
history = model.fit(db, epochs=5, validation_data=ds_val, validation_freq=1)
"""
模型训练的次数是5,每1次循环进行测试
"""

6.9 模型保存

以.h5文件格式保存模型

"6.模型保存"
model.save('ann_mnist.h5')  # 以.h5文件格式保存模型

6.10 模型评价

得到测试集的正确率

"7.模型评价"
model.evaluate(ds_val)  # 得到测试集的正确率

6.11 模型测试

对模型进行测试

"8.模型测试"
sample = next(iter(ds_val))  # 取一个batchsz的测试集数据
x = sample[0]  # 测试集数据
y = sample[1]  # 测试集的标签
pred = model.predict(x)  # 将一个batchsz的测试集数据输入神经网络的结果
pred = tf.argmax(pred, axis=1)  # 每个预测的结果的概率最大值的下标,也就是预测的数字
y = tf.argmax(y, axis=1)  # 每个标签的最大值对应的下标,也就是标签对应的数字
print(pred)  # 打印预测结果
print(y)  # 打印标签数字

6.12 模型训练结果的可视化

对模型的训练结果进行可视化

"9.模型训练时的可视化"
# 显示训练集和验证集的acc和loss曲线
acc = history.history['accuracy']  # 获取模型训练中的accuracy
val_acc = history.history['val_accuracy']  # 获取模型训练中的val_accuracy
loss = history.history['loss']  # 获取模型训练中的loss
val_loss = history.history['val_loss']  # 获取模型训练中的val_loss
# 绘值acc曲线
plt.figure(1)
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.legend()
# 绘制loss曲线
plt.figure(2)
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()  # 将结果显示出来

7. 手写数字识别的ANN模型可视化结果图

Epoch 1/5
469/469 [==============================] - 5s 6ms/step - loss: 0.2726 - accuracy: 0.9186 - val_loss: 0.1712 - val_accuracy: 0.9542
Epoch 2/5
469/469 [==============================] - 3s 5ms/step - loss: 0.1341 - accuracy: 0.9632 - val_loss: 0.1232 - val_accuracy: 0.9654
Epoch 3/5
469/469 [==============================] - 3s 5ms/step - loss: 0.1126 - accuracy: 0.9691 - val_loss: 0.1032 - val_accuracy: 0.9702
Epoch 4/5
469/469 [==============================] - 3s 5ms/step - loss: 0.0926 - accuracy: 0.9750 - val_loss: 0.1217 - val_accuracy: 0.9690
Epoch 5/5
469/469 [==============================] - 3s 5ms/step - loss: 0.0900 - accuracy: 0.9759 - val_loss: 0.1246 - val_accuracy: 0.9676

从以上结果可知，模型的准确率达到了96%。

8. 完整代码

# 导入tensorflow
import tensorflow as tf
# 导入keras
from tensorflow import keras
# 引入内置手写体数据集mnist
from keras.datasets import mnist
# 引入绘制acc和loss曲线的库
import matplotlib.pyplot as plt
# 引入ANN的必要的类
from keras.layers import Dense
from keras.models import Sequential
from keras import optimizers, losses

"1.加载数据"
"""
x_train是mnist训练集图片,大小的28*28的,y_train是对应的标签是数字
x_test是mnist测试集图片,大小的28*28的,y_test是对应的标签是数字
"""
(x_train, y_train), (x_test, y_test) = mnist.load_data()  # 加载mnist数据集
print('mnist_data:', x_train.shape, y_train.shape, x_test.shape, y_test.shape)  # 打印训练数据和测试数据的形状

"2.数据预处理"


def preprocess(x, y):  # 数据预处理函数
    x = tf.cast(x, dtype=tf.float32) / 255.  # 将输入的图片进行归一化，从0-255变换到0-1
    x = tf.reshape(x, [28 * 28])
    """
    # 将输入图片的形状(60000,28,28)转换成(60000,28*28),
    相当于将图片拉直,便于输入给神经网络
    """
    y = tf.cast(y, dtype=tf.int32)  # 将输入图片的标签转换为int32类型
    y = tf.one_hot(y, depth=10)
    """
    # 将标签y进行独热编码,因为神经网络的输出是10个概率值,而y是1个数，
    计算loss时无法对应计算,因此将y进行独立编码成为10个数的行向量，然后进行loss的计算
    独热编码:例如数值1的10分类的独热编码是[0 1 0 0 0 0 0 0 0 0,即1的位置为1，其余位置为0
    """
    return x, y


batchsz = 128  # 每次输入给神经网络的图片数
"""
数据加载进入内存后，需要转换成 Dataset 对象，才能利用 TensorFlow 提供的各种便捷功能。
通过 Dataset.from_tensor_slices 可以将训练部分的数据图片 x 和标签 y 都转换成Dataset 对象
"""
db = tf.data.Dataset.from_tensor_slices((x_train, y_train))  # 构建训练集对象
db = db.map(preprocess).shuffle(60000).batch(batchsz)  # 将数据进行预处理，随机打散和批量处理
ds_val = tf.data.Dataset.from_tensor_slices((x_test, y_test))  # 构建测试集对象
ds_val = ds_val.map(preprocess).batch(batchsz)  # 将数据进行预处理，随机打散和批量处理

"3.构建网络模型"
model = Sequential([Dense(256, activation='relu'),
                      Dense(128, activation='relu'),
                      Dense(64, activation='relu'),
                      Dense(32, activation='relu'),
                      Dense(10,activation='softmax')])
"""
构建了5层ANN网络,每层的神经元个数分别是256,128,64,32,10,
隐藏层的激活函数是relu,输出层的激活函数是sortmax
"""
model.build(input_shape=(None, 28 * 28))  # 模型的输入大小
model.summary()  # 打印网络结构

"4.模型编译"
model.compile(optimizer=optimizers.Adam(lr=0.01),
                loss=tf.losses.CategoricalCrossentropy(from_logits=False),
                metrics=['accuracy']
                )
"""
模型的优化器是Adam,学习率是0.01,
损失函数是losses.CategoricalCrossentropy,
性能指标是正确率accuracy
"""

"5.模型训练"
history = model.fit(db, epochs=5, validation_data=ds_val, validation_freq=1)
"""
模型训练的次数是5,每1次循环进行测试
"""
"6.模型保存"
model.save('ann_mnist.h5')  # 以.h5文件格式保存模型

"7.模型评价"
model.evaluate(ds_val)  # 得到测试集的正确率

"8.模型测试"
sample = next(iter(ds_val))  # 取一个batchsz的测试集数据
x = sample[0]  # 测试集数据
y = sample[1]  # 测试集的标签
pred = model.predict(x)  # 将一个batchsz的测试集数据输入神经网络的结果
pred = tf.argmax(pred, axis=1)  # 每个预测的结果的概率最大值的下标,也就是预测的数字
y = tf.argmax(y, axis=1)  # 每个标签的最大值对应的下标,也就是标签对应的数字
print(pred)  # 打印预测结果
print(y)  # 打印标签数字

"9.模型训练时的可视化"
# 显示训练集和验证集的acc和loss曲线
acc = history.history['accuracy']  # 获取模型训练中的accuracy
val_acc = history.history['val_accuracy']  # 获取模型训练中的val_accuracy
loss = history.history['loss']  # 获取模型训练中的loss
val_loss = history.history['val_loss']  # 获取模型训练中的val_loss
# 绘值acc曲线
plt.figure(1)
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.legend()
# 绘制loss曲线
plt.figure(2)
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()  # 将结果显示出来