二叉树 — 返回最大的二叉搜索子树大小

题目：
给定一棵二叉树的head节点，返回这颗二叉树中最大的二叉搜索子树的大小。
一颗二叉树来讲，可能整棵树不是搜索二叉树，但子树是一颗搜索二叉树。如下图所示，这时要返回这颗子搜索二叉树的最大节点个数。下图中，最大的二叉搜索子树大小为：3（5 -> 1 -> 7）。

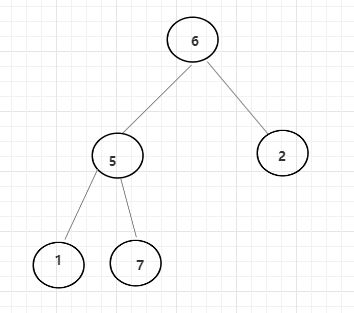
子树的概念是：每个单独节点算一棵子树， 5 -> 1 -> 7三个节点算一棵子树（不可以舍弃任何一个）
1 -> 5 -> 7 -> 6 -> 2同样也算一棵子树，同样不可以舍弃任何一个节点。

递归方式

1. 只有左树满足二叉搜索树的情况
2. 只有右树满足二叉搜索树的情况
3. 整棵树都是二叉搜索树的情况
4. 判断是否是二叉搜索树需要左右子树max、min的值和当前值节点值进行比较，如果左树最大值小于当前值，右树最小值大于当前值，则说明是一颗二叉搜索树
5. 需要整棵树的节点数变量（allSize）和满足子树最大二叉搜索树节点数变量（maxBSTSubtreeSize），如果两个值相等，说明是二叉搜索树，如果不相等，则说明不是（用这两个值在构建Info信息类时，可省略一个bollean isBST的变量）。
6. 根据4、5的要求构建Info对象，递归调用并收集左右子节点的Info信息进行判断。

代码：
Info类用于收集树的信息，并通过递归返回给上层，供上层调用进行分析。

public static class Info{
        int max;
        int min;
        int allSize;
        //满足子树是二叉搜索树最大节点个数
        int maxBSTSubtreeSize;

        public Info(int maxBSTSubtreeSize,int allSize,int max,int min){
            this.maxBSTSubtreeSize = maxBSTSubtreeSize;
            this.allSize = allSize;
            this.max = max;
            this.min = min;
        }
    }

public static int largestBSTSubtree(Node head){
        if(head == null){
            return 0;
        }

        return process(head).maxBSTSubtreeSize;
    }

     //       6
    //    2      7
    // 1    5
    public static Info process(Node head){
        //如果节点为null，不方便构建Info对象信息，所以返回null，下面要对Info对象进行非null判断。
        if (head == null){
            return null;
        }

        Info leftInfo = process(head.left);
        Info rightInfo = process(head.right);

        int max = head.val;
        int min = head.val;
        int allSize = 1;

        if (leftInfo != null){
            max = Math.max(max,leftInfo.max);
            min = Math.min(min,leftInfo.min);
            allSize += leftInfo.allSize;
        }

        if (rightInfo != null){
            max = Math.max(max,rightInfo.max);
            min = Math.min(min,rightInfo.min);
            allSize += rightInfo.allSize;
        }
        //p为每棵树的满足二叉搜索树的节点个数。
        
        //如果左子树不为null，则修改 p1 为 左子树的最大二叉搜索树的个数
        int p1 = -1;
        if (leftInfo != null){
            p1 = leftInfo.maxBSTSubtreeSize;
        }

        //如果右树不为null， 则修改 p2 为 右子树的最大二叉搜索树的个数
        int p2 = -1;
        if (rightInfo != null){
            p2 = rightInfo.maxBSTSubtreeSize;
        }
        
        //只有在左右子树都满足是二叉搜索树的情况下，才更新p3。
        int p3 = -1;
        //左右子树的最大二叉搜索树的个数 = 左右子树整棵树的个数，则说明为二叉搜索树。
        //如果maxBSTSubtreeSize ！= allSize 则说明之前遍历左右树过程中，出现了 左树最大值 > 当前节点 或 右树最小值 < 当前节点的情况
        boolean isBSTLeft = leftInfo == null ? true : (leftInfo.maxBSTSubtreeSize == leftInfo.allSize);
        boolean isSBTRight = rightInfo == null ? true : (rightInfo.maxBSTSubtreeSize == rightInfo.allSize);

        if (isBSTLeft && isSBTRight){
            //看左子树的最大值 是否小于当前树的值
            //看右子树的最小值 是否小于当前数的值
            boolean leftMaxLessX = leftInfo == null ? true : (leftInfo.max < head.val);
            boolean rightMinMoreX = rightInfo == null ? true : (rightInfo.min > head.val);
			//只有在左右子节点都是二叉搜索树的情况下，更新p3.
            if (leftMaxLessX &&  rightMinMoreX){
                int leftSize = leftInfo == null ? 0 : leftInfo.allSize;
                int rightSize = rightInfo == null ? 0 : rightInfo.allSize;
                p3 = leftSize + rightSize + 1;
            }
        }
        return new Info(Math.max(p3,Math.max(p1,p2)),allSize,max,min);
    }

暴力方式

1. 将生成的二叉树进行中序遍历（左、头、右）并放进List或Array中
2. 遍历集合，如果集合中的元素依次都是有小到大的顺序，那说明整棵树都是二叉搜索树（左节点最大值 < 头节点 < 右节点最小值），那直接return 集合的大小。
3. 如果不满足依次由小到大的顺序，则递归，左右子树找到满足条件的二叉搜索树，并通过Max.math选择较大的一个。

代码

 private static void in(Node head, List<Node> list) {
        if (head == null) {
            return;
        }
        in(head.left, list);
        list.add(head);
        in(head.right, list);
    }
    
private static int largestBSTSubtree1(Node head) {
        if (head == null) {
            return 0;
        }
        List<Node> list = new ArrayList<>();
        //中序遍历
        in(head, list);
        for (int i = 1; i < list.size(); i++) {
            if (list.get(i).val <= list.get(i - 1).val) {
               int leftRes =  largestBSTSubtree1(head.left);
               int rightRes =  largestBSTSubtree1(head.right);
               return Math.max(leftRes,rightRes);
            }
        }
        return list.size();
    }

对数器
递归生成随机二叉树

public static Node generateRandomNode(int maxLength, int maxValue) {
        return generateNode(1, maxLength, maxValue);
    }

    public static Node generateNode(int level, int maxLength, int maxValue) {
        if (level > maxLength || Math.random() < 0.5) {
            return null;
        }
        Node head = new Node((int) (Math.random() * maxValue));
        head.left = generateNode(level + 1, maxLength, maxValue);
        head.right = generateNode(level + 1, maxLength, maxValue);
        return head;
    }

测试

 public static void main(String[] args) {
 		//通过大样本数据量进行测试，如果i1 ！= i2说明有问题，
        int maxValue = 100;
        int maxLength = 50;
        int testNum = 100000;
        for (int i = 0; i < testNum; i++) {
            Node head = generateRandomNode(maxLength, maxValue);
            int i1 = largestBSTSubtree1(head);
            int i2 = largestBSTSubtree2(head);
            if (i1 != i2){
                System.out.println("Fucking Fuck!!!");
                break;
            }
        }
        System.out.println("finish");
    }