C/C++数据在计算机内存中的存储形式详解

目录：

        一，基础的数据存储形式

        二，整型提升的数据形式

        三，浮点型的存储形式

---

一，基础的数据存储形式

1，整数存储的基础介绍

        为什么要介绍整型数据呢？因为整型类数据的存储形式比较简单，是所有数据中的存储形式最简单的一个，也是最为基础的一个，所有的数据存储基本都要以次为基础。

        首先，要明白的是，计算机存储数据都是以二进制存储的，。整数分为正数，负数和0。正数和0的存储形式是直接转为二进制形式存储，而最高位要为0，代表正数，即为符号位，而负数的存储形式是先将其转为二进制，最高位为1，代表负数，即符号位，然后加一，最后符号位不变，其它位取反，即补码。其他数据类型也是以此为基础的，只是有些数据在形式复杂了一点

（因为这一原理比较简单，在这里我就不做过多解释了）

2，大小端的存储形式

        在介绍大端和小端前，我们先认识一下高字节位和低字节位，高地址和低地址。

        我们以32位平台的机器为例：

 高字节和低字节：

        以上我们是以十六进制为例，其他进制原理也是一样，高字节和低字节的方式都是占据在“高位”上，低字节在“低位”上。

高地址和低地址：

        根据上次讲解的指针知识，可得出，内存中一个地址所蕴含的空间为1字节，而当向内存申请一个空间时，一系列数据是从上面往下面填充的，即上面的内存叫做低地址，下面的叫做高地址。

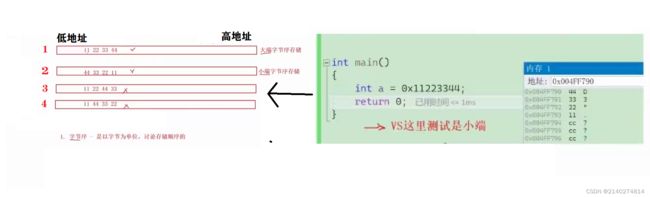
大端和小端

        大端和小端是一种字节序存储方式：

        大端字节序存储：把一个数据的高位字节的内容放到低地址处，把一个数据的低位字节内容放到高地址处

        小端字节序存储：把一个数据的低位字节的内容放到低地址处，把一个数据的高位字节内容放到高地址处

注意：没有图上的3和4字节序的存储方式，基本都已大端字节序和小端字节序来存储

---

二，整型提升的数据形式

        整型提升可很好的解释当数据类型存储不下数据的时候打印出的莫名其妙的数据，下面，我以char类型来进行讲解整型提升

        char类型最多存储为1字节，即8个比特位，经过上面整型的讲解可知，存储数据的最高二进制位为符号位，但若用无符号存储时，就没有符号位了，即所有的位都会被计算机算进去。由此可知，当有符号存储时数据的范围是[-128,127]，无符号存储的范围是[0,255]。

        以32位机器为例，当一个数据被存储时，机器是先将数据放入内存中存储或运算，而存储的形式位补码，当机器对其运算或存储结束后，因char类型只能存储8位，所以会将二进制进行截断，从截断低字节位开始，截断8位放到char类型中存储，最后在放入机器中进行整型提升，即若是有符号类型，在高字节位补上与符号位相同的数字，若是无符号类型，则补0，一共32位。

下面我代码的形式进行详细的讲述：

#include
int main()
{
    char a = 5;
    //00000000000000000000000000000101 原码==补码==反码
    //00000101  机器给予char，让char存储，发生截断，截断8位
    //00000101  原码==补码==反码，为最终结果，数值为5
    char b = 127;
    //00000000000000000000000001111111 原码==补码==反码
    //01111111    机器给予char，让char存储，发生截断，截断8位
    //01111111    原码==补码==反码，为最终结果，数值为127
    char c = a + b;
    //00000000000000000000000010000100 同理
    //10000100 同理
    //11111111111111111111111110000100  整型提升，有符号位，往高字节位补符号位
    // 可看出，最高位位1，为负数，将其转化为原码后输出
    //11111111111111111111111110000011 反码
    //10000000000000000000000001111100 原码，数值为-124
    printf("%d %d %d", a, b, c);
    return 0;
}

输出结果：

 其他类型或数据与之同理。

        接下来稍微深入一下，如果当我们无符号输出的时候会怎么样？其中方法类似，只不过此时没有符号位，即默认位正数，再整型提升的时候和输出的时候原理与正数整型提升的情况一样，著不过需注意的是，刚开始存储的时候，数据是先放入32位机器的内部形式存储，此时机器仍然按照负数的形式存储，当放入存储类型的时候，才按照类型数据自己的存储方式进行存放，最后在由32位机器的内部形式输出。

下面是我还以代码的形式跟读者们演示一下：

#include
int main()
{
    char a = -1;//此形式默认为有符号形式
    //10000000000000000000000000000001 原码
    //11111111111111111111111111111110 反码
    //11111111111111111111111111111111 补码
    //11111111 截断，放到char类型中存储
    //11111111111111111111111111111111 整型提升
    //11111111111111111111111111111110 反码
    //10000000000000000000000000000001 原码
    //此时原码为最终数据，值为-1
    signed char b = -1;//有符号类型存储，与上述情况一样
    unsigned char c = -1;//无符号类型存储，默认最高位为符号位
    //注意：数据是先放入32位机器的内部形式存储，此时机器仍然按照负数的形式存储
    //10000000000000000000000000000001 原码
    //11111111111111111111111111111110 反码
    //11111111111111111111111111111111 补码
    //11111111 截断，放到unsigned char类型中存储,此时为无符号形式存储
    //00000000000000000000000011111111 整型提升，高字节位补0
    //因为是无符号形式，放入32位机器内部中以无符号形式输出结果
    //00000000000000000000000011111111 此时，原码==补码==反码，数值为255
    printf("%d %d %d", a, b, c);
    //最后补充一点：%d为有符号输出，%u为无符号输出
    return 0;
}

运行图：

         有了以上的知识，无符号的输出（%u）就简单多了，形式上与上面一样，最后只不过将数据的二进制位全部算入进去为最终结果。

        根据上面：我们很容易证明出，当数据类型可以存储的下时，有符号操作将会正常输出，无 符号操作的非负数将正常输出。（可以在纸上证明一下，因为这一点知识会用即可，我就不做过多证明）

 以下是用代码进行的规律总结：

//对于char的整型提升的规律
#include
int main()
{
    char a = 128, b = 129, c = 130;
//char类型在[-128,127]之间，若在127往后增大会在-128，-127..0..127..-128循环
//若在-128往后减小，即-129时a=127,126..0,-1..-128,127循环
    printf("%d %d %d", a, b, c);//输出-128， -127， -126
    return 0;
}

---

三，浮点型的存储形式   

        整型与浮点型在内存中的存储方式是有差异的。对于内存，浮点数V=(-1)^S*M*2^E，其中：S=0或1(0代表这个数是正数，1代表这个数是负数)，1<=M<2，E为指数(注意：E可正可负)，计算机在存储浮点数时只存储S,M,E。例如：5.5(d)=101.1(b)=(-1)^0*1.011*2^2，其中S=0，M=1.011，E=2。0.5(d)=(-1)^0*1.0*2^(-1)，其中S=0,M=1.0,E=-1。而对于S,M,E的存储形式如下图：

 M的存储方式：

        其中，IEEE 754对有效M和N还有一些特别规定。在计算机的内部保存M时，默认这个数的第一位为1，因此可以被舍去，只保留后面的部分，等到读取的时候，再把第一位的1加上去，这样做的目的是节省1位有效数字。以32位机器为例，留给M的只有23位，而将1舍去后，等于可以保存24位有效数字。

E的存储方式：

        首先，当E为正数的时，若E的存储为8位，它的取值范围为[0,255]，若E的存储为11位，它的取值范围为[0,2047]。当E为负数时，若E的存储为8位，要先加上127，若E的存储为11位，要先加上1023，随后再往机器中存储。例如：当为32位机器时，2^10中的E为10，127+10=137，即机器中存储的是137的二进制序列：10001001。

        当从内存中取出E时，分三种情况：

        1，当E不全为0或不全为1

                此时，E按照正常思维，将其值减去127或1023，而M正常加1

        2，当E全为0

                这时，指数E等于1-127=-126或1-1023=-1022，此时，M不在加上1。因为当E全为                  0 时，即此时存入内存中的E真实值为-127，可得出，这个浮点数几乎为0，因此，计算机              这样做是为了表示无限接近于0

        3，当E全为1

                这是，刚开始存入内存中的E的数值非常大，此时的浮点数表无穷大或无穷小

        我们只需明白第一种情况即可，全为1或0的情况只需了解就行，这种情况不做为重点，这里我就不做过多解释了

下面，我以代码的形式跟大家详细解释一下

//在32位平台上存储浮点型数据的情况
#include
int main()
{
    float a = 5.5;
    //5.5的二进制形式为101.1=(-1)^0+1.011*2^2
    //M = 1.011, E = 2, S = 0;
    //存储形式为0 10000001 01100000000000000000000
    //即：01000000101100000000000000000000==0x40b00000
    return 0;
}
 

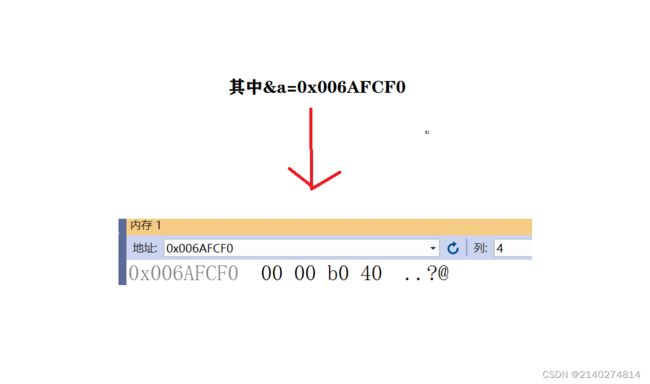
在vs上调试的内存监视上看如下：

        最后序需提醒的是，有些浮点数在内存中以二进制的形似比较难以准确表达，只能无限的接近于这个数，而在内存中有只存储S，M，E，所以，当表示有些浮点数时，会出现小小的误差。 

下面，我们运用这一原理来解释一个代码

#include
int main()
{
    int n = 9;
    float* p = (float*)&n;//在内存中将会运用浮点型的存储方式

// n的存储为0 00000000 00000000000000000001001==9

//此时的浮点型*p存储数据S=0       E=-126       M=0.00000000000000000001001

//即此时的*p==(-1)^0*0.00000000000000000001001*2^-126
    printf("n=%d\n", n);
    //因为p是用浮点型进行存储的，所以打印的数值将不再是9
    printf("*p=%f\n", *p);//%f默认保留小数点后六位，所以为0.000000
    *p = 9.0;

//此时对应存储地址对应的空间已经完全发生了变化，将会按照浮点型方式来存储的，所以当用整形方式来输出的时候将会有差异

//9.0(d)==1001.0(b)==1.001*2^3==(-1)^0*1.001*2^3

//S=0       E=3      M=1.001

//0     10000010   00100000000000000000000

//即存储形式为：01000001000100000000000000000000  原码=反码=补码

//即数值上等于1091567616为最终结果
    printf("n=%d\n", n);//输出1091567616
    printf("*p=%f\n", *p);//按照浮点型存储，正常打印9.000000
    return 0;
}

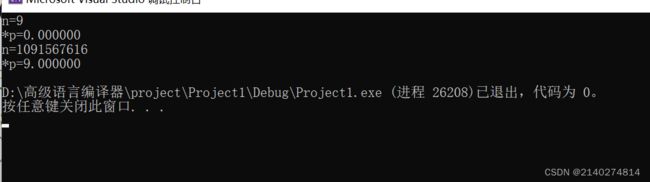
输出结果如图：

       注意：当我们运用强制类型转换时，数据是先转化后在放入数据类型中给予内存中储存，如以下代码。

#include
int main()
{
    int b = 9;
    float* a = (float*)&b;//将其地址用浮点型存储，将会运用浮点型的存储方式
    float c = b;
    float d = (float)b;
    //注意：其实浮点数不等于0，因为纸打印小数点后六位，所以为0
    printf("%d %f\n", b, *a);//输出9 0.000000
    //都将输出9，属于强制转化，将其转化后直接在存储9，不属于在浮点型存储的存储形式
    printf("%.0f %.0f", c, d);//输出9 9
    return 0;
}

本次的介绍已完毕，感谢大家支持，欢迎随时留言评论