快排(非递归)

简介

在我们学习排序的时候一定接触过快排这个较优的排序,那么既然已经有这个排序了为什么还要去学习一个非递归的快速排序呢,设想一下,快排是利用了递归的思想,所以在排序的时候会占用大量的栈帧空间,如果处理不妥可能会造成数据溢出等一些情况,那么改为非递归就完全不用担心这个问题,这里我们要学习的不仅仅是快排的非递归,更多的是一种非递归的思想,假设你去某个公司上班,发现某段程序在一些特定的情况下会有溢出的情况,那么如何去优化就显得很重要。

非递归思想

在这里，我们先对比一下快排，快排的思想是找出一个数作为基数，然后以这个基数来划分，把小于基数的数放左边，大于基数的数放右边，那么在非递归的时候我们同样可以利用这个特性，但是在利用这个特性的时候就会用到空间，我们不可能去开辟一大堆空间来事前做准备吧。那么这里就可以利用到我们的栈来模拟递归的过程。

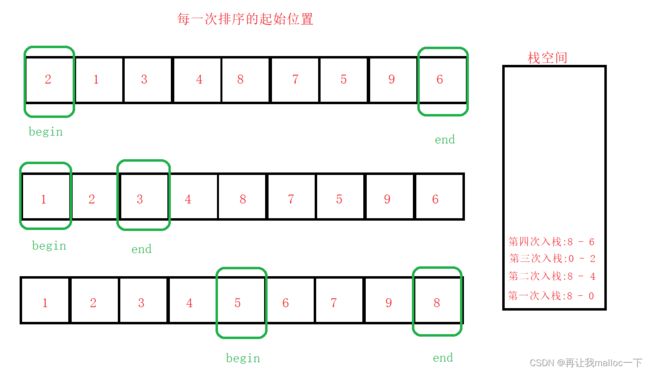
设想一下，我们当前有一块栈的空间，我们去模拟快排在排序过程中的划分区域的动作，先把right和left依次入栈

 入栈之后我们开始划分，利用快排里面的前后指针排序的方法进行单趟排序。

前后指针单趟排序

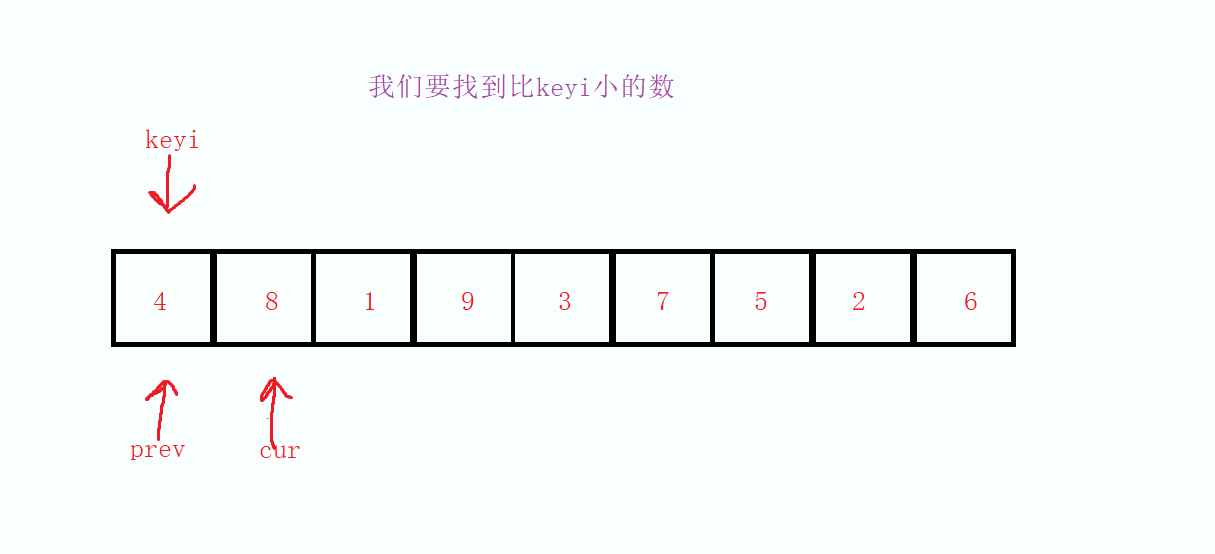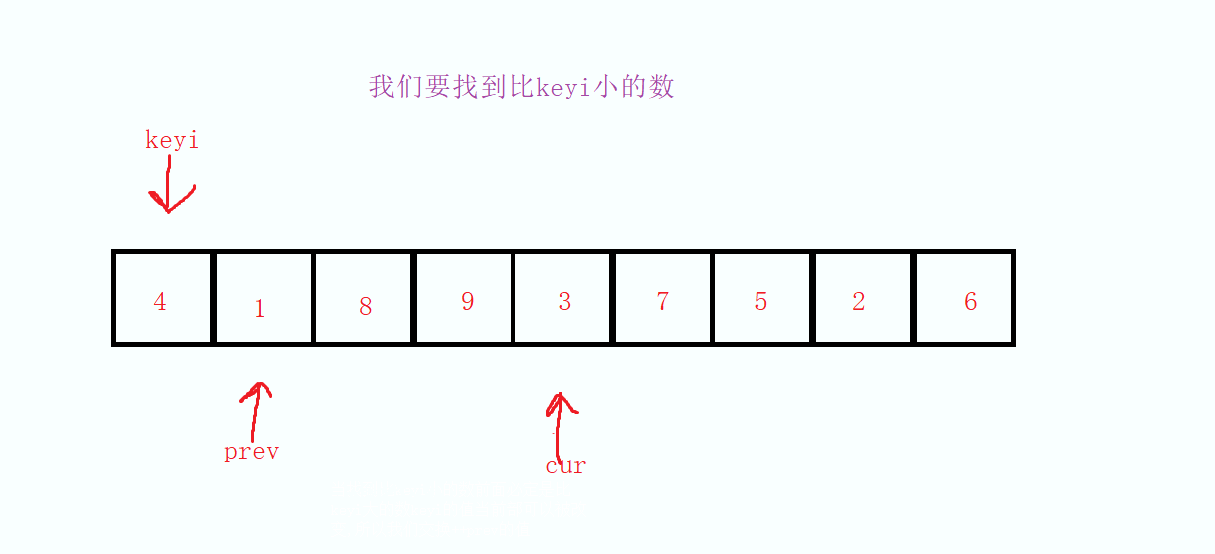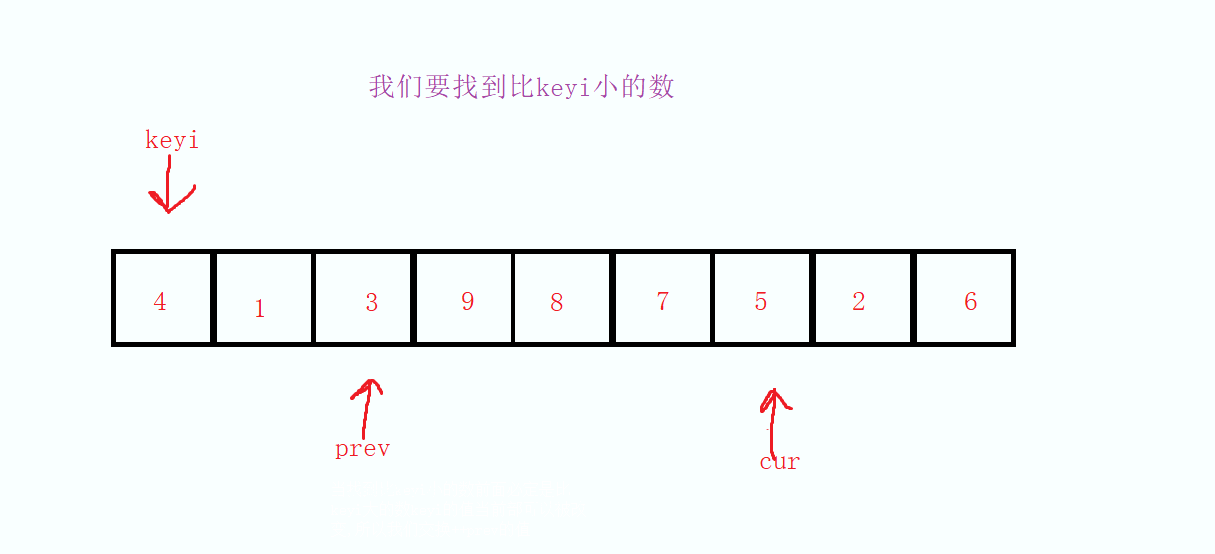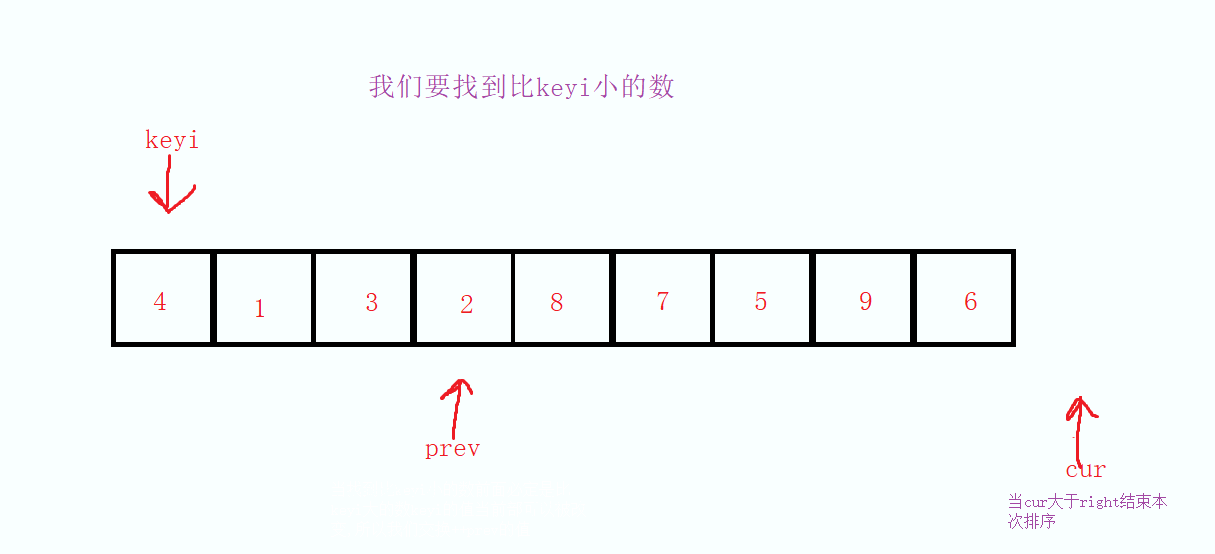
我们定义三个变量为keyi，prev和cur，keyi，prev从起始位置开始，cur从起始位置的下一个位置开始，当cur指向的值小于keyi的时候，因为cur走过的值是一定比keyi大的，所以当我们找到了比keyi小的数的时候先对prev进项自增操作，然后把cur的值和prev的值进行交换

 然后依次重复这样的操作，直到最后cur大于right 的时候结束本次循环，最后因为prev的值必定是比keyi的值大的，所以在将keyi的值和prev的值进行交换，在将keyi和prev的下标交换，最后返回keyi，这样就达成第一次的分割数据。

当第一次数据分割完成之后我们就可以开始第二次分割，以keyi作为分界点，因为左边必定

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
#include

typedef int STDataType;

typedef struct Stack
{
	STDataType* n;
	STDataType top;
	STDataType capacity; 
}ST;

void STInit(ST* ps);

void STDestroy(ST* ps);

void STPush(ST* n,STDataType x);

void STPop(ST* n);

int STSize(ST* n);

bool STEmpty(ST* n);

int STTOP(ST* n);

void QucikSortR(int* a, int left, int right);



#define _CRT_SECURE_NO_WARNINGS 1
#include"Stack.h"

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void STInit(ST* ps)
{
	ps->n = (STDataType*)malloc(sizeof(STDataType) * 4);
	if (ps->n == NULL)
	{
		perror("malloc:>");
		return;
	}
	ps->capacity = 4;
	ps->top = 0;
}

void STPush(ST* ps, STDataType x)
{
	assert(ps);
	ST* tmp = ps;
	if (ps->top == ps->capacity)
	{
		tmp->n = (STDataType*)realloc(ps->n, sizeof(STDataType) * ps->capacity*2);
		if (tmp->n == NULL)
		{
			perror("realloc:>");
			return;
		}
		ps = tmp;
		ps->capacity *= 2;
	}
	ps->n[ps->top] = x;
	ps->top++;
}

void STPop(ST* ps)
{
	assert(ps);
	assert(!STEmpty(ps));
	ps->top--;
}

int STSize(ST* ps)
{
	assert(ps);
	return ps->top;
}


bool STEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

int STTOP(ST* ps)
{
	assert(ps);
	assert(!STEmpty(ps));
	return ps->n[ps->top-1];
}

void STDestroy(ST* ps)
{
	free(ps->n);
	ps->n = NULL;
	ps->capacity = 0;
	ps->top = 0;
}


int GetMidNumi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

//单趟排序
int PartSort3(int* a, int left, int right)
{
	// 三数取中
	int midi = GetMidNumi(a, left, right);
	if (midi != left)
		Swap(&a[midi], &a[left]);

	int keyi = left;

	int prev = left;
	int cur = left + 1;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && ++prev != cur)//如果cur的值小于prev并且++prev不能等于cur就交换两个值,因为相等的话交换之后是无意义
			Swap(&a[cur], &a[prev]);

		++cur;//如果cur大于prev的话cur继续++直到找到或者不满足条件
	}

	Swap(&a[prev], &a[keyi]);//数据最后分割到之后两个并且++prev的值是等于cur的所以就交换他们两个的值
	keyi = prev;//让prev作为keyi继续分割

	return keyi;
}


void QucikSortR(int* a, int left, int right)
{
	ST st;
	STInit(&st);
	STPush(&st, right);
	STPush(&st, left);

	while (!STEmpty(&st))
	{
		int begin = STTOP(&st);
		STPop(&st);
		int end = STTOP(&st);
		STPop(&st);
		int keyi = PartSort3(a, begin, end);//第一趟把小于keyi的放左边,大于keyi的放右边

		if (keyi + 1 < end) //当分割到最后keyi+1大于等于end的时候就说明只有一个数据所以是不需要进行排序的
		{
			STPush(&st, end);
			STPush(&st, keyi+1);
		}
		if (begin < keyi-1)//当分割到最后keyi+1小于等于begin的时候就说明只有一个数据所以是不需要进行排序的
		{
			STPush(&st, keyi-1);
			STPush(&st, begin);
		}
	}
	STDestroy(&st);
}


#define _CRT_SECURE_NO_WARNINGS 1
#include"Stack.h"
int main()
{
	int arr[] = { 4,8,1,9,3,7,5,2,6};
	int sz = sizeof(arr) / sizeof(arr[0]);
	QucikSortR(arr, 0, sz - 1);
	for (int i = 0; i < sz; i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

小于keyi右边必定大于keyi，继续刚才的操作，每次排序好一个，最后结合起来的时候所有数都是有序的。