数据结构——栈与队列
目录
一、栈
1.栈的定义
2.栈的分类与基本操作
1. 顺序栈
2.链栈
3.栈与递归的实现
1.递归的简单描述
2.递归过程及与栈的关联
3.递归过程示意图
二.队列
1.队列的定义
2.队列的分类与基本操作
1.顺序队列
2.链队列
3.循环队列
1.假溢出
2.循环队列
3.循环队列相关操作实现:
栈和队列是两种重要的线性结构。从数据结构的角度来看,栈与队列均属于线性表,其特殊性在于栈与队列的基本操作为线性表基本操作的子集,栈与队列为操作受限的线性表,故,栈与队列可称为限定性的数据结构,
一、栈
1.栈的定义
栈,是限定仅在表尾进行插入与删除操作的线性表。对于栈来说,表尾端具有特殊的含义,称为栈顶,相应地将表头段成为栈底。不含元素的空表称为空栈。
栈的修改是按照后进先出的原则进行的,因此将栈成为后进先出的线性表。
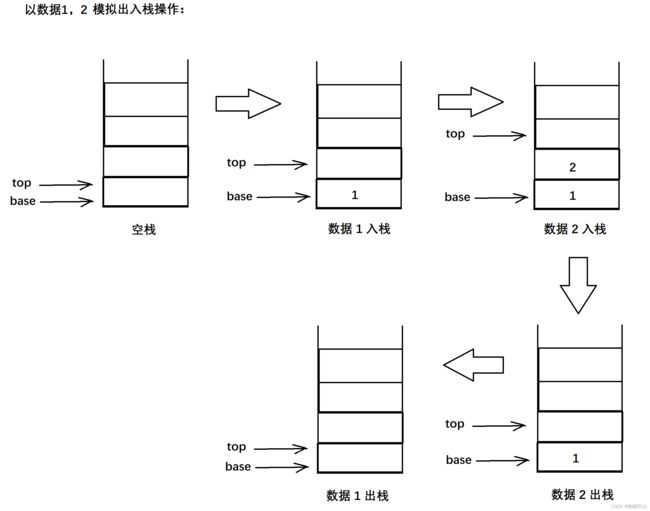
栈的示意图:
模拟实现出栈与入栈操作:(以顺序栈为例)
2.栈的分类与基本操作
栈有两种存储表示方式:顺序存储方式与链式存储方式
1. 顺序栈
栈的顺序存储结构是利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素,同时附设指针top指示栈顶元素在顺序栈中的位置(位置应与数据在顺序表中的下标区分理解)。
一种定义顺序栈的常用方法:先为栈分配一个初始容量,在实际应用过程中,当栈的存储空间不够时再逐段扩容。
以下为顺序栈的相关基本操作:
方法1:
#include
#include
#include
#include
#define Stack_Init_Size 10
#define Stack_Add_Size 5
//定义顺序栈的结构体
typedef int ElemType;
typedef struct Stack
{
ElemType* base; //定义栈底指针
ElemType* top; //定义栈顶指针
int capacity; //指明当前栈的容量
}Stack;
//栈的初始化操作
void StackInit(Stack* ps)
{
ps->base = (ElemType*)malloc(sizeof(ElemType) * Stack_Init_Size);
if (NULL == ps->base) //空间申请失败处理
{
printf("空间申请失败\n");
exit(0);
}
ps->top = ps->base;
ps->capacity = Stack_Init_Size;
}
//栈的判空操作
bool StackIsEmpty(Stack* ps)
{
return ps->base == ps->top ? true : false;
}
//当前栈内元素数量
int StackNum(Stack* ps)
{
return ps->top - ps->base;
}
//获取栈顶元素
void GetTop(Stack* ps, ElemType* e)
{
assert(ps);
if (ps->base == ps->top)
{
printf("当前栈中无元素\n");
return;
}
*e = *(ps->top - 1);
}
//出栈
void StackPop(Stack* ps, ElemType* e)
{
assert(ps);
if (ps->base == ps->top)
{
printf("当前栈中无元素\n");
exit(0);
}
*e = *(--ps->top);
}
//检查栈是否需要扩容
void StackCheckCapacity(Stack* ps)
{
assert(ps);
if (ps->top - ps->base >= ps->capacity)
{
ps->base = (ElemType*)realloc(ps->base, sizeof(ElemType) * (ps->capacity + Stack_Add_Size));
if (NULL == ps->base)
{
printf("空间申请失败\n");
exit(0);
}
ps->top = ps->base + ps->capacity;
ps->capacity += Stack_Add_Size;
}
}
//入栈
void StackPush(Stack* ps, ElemType e)
{
assert(ps);
StackCheckCapacity(ps);
*(ps->top++) = e;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
if (ps->base)
{
free(ps->base);
ps->base = NULL;
ps->capacity = 0;
}
} 方法2:
#include
#include
#include
#define Stack_Init_Size 10
#define Stack_Add_Size 5
typedef int ElemType;
typedef struct Stack
{
ElemType* data;
int top; // 栈顶
int capacity; // 容量
}Stack;
// 初始化栈
void StackInit(Stack* ps)
{
ps->data = (ElemType*)malloc(sizeof(ElemType) * Stack_Init_Size);
if (NULL == ps->data)
{
printf("空间申请失败\n");
exit(0);
}
ps->capacity = Stack_Init_Size;
ps->top = 0;
}
//扩容判断
void CapacityCheck(Stack* ps)
{
assert(ps);
if (ps->top >= ps->capacity)
{
ps->data = (ElemType*)realloc(sizeof(ElemType) * (ps->capacity + Stack_Add_Size));
if (NULL == ps->data)
{
printf("空间申请失败\n");
exit(0);
}
ps->capacity += Stack_Add_Size;
}
}
// 入栈
void StackPush(Stack* ps, ElemType data)
{
assert(ps);
CapacityCheck(ps);
ps->data[ps->top++] = data;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
if (ps->top == 0)
{
printf("当前栈中无元素\n");
return;
}
ps->top--;
}
// 获取栈顶元素
ElemType StackTop(Stack* ps)
{
assert(ps);
if (ps->top == 0)
{
printf("当前栈中无元素\n");
return;
}
return ps->data[ps->top - 1];
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
return ps->top;
}
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
int StackEmpty(Stack* ps)
{
return ps->top == 0 ? 1 : 0;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
if (ps->data)
{
free(ps->data);
ps->data = NULL;
ps->capacity = 0;
ps->top = 0;
}
} 2.链栈
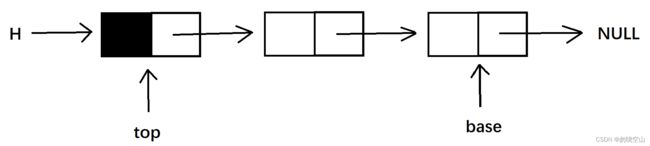
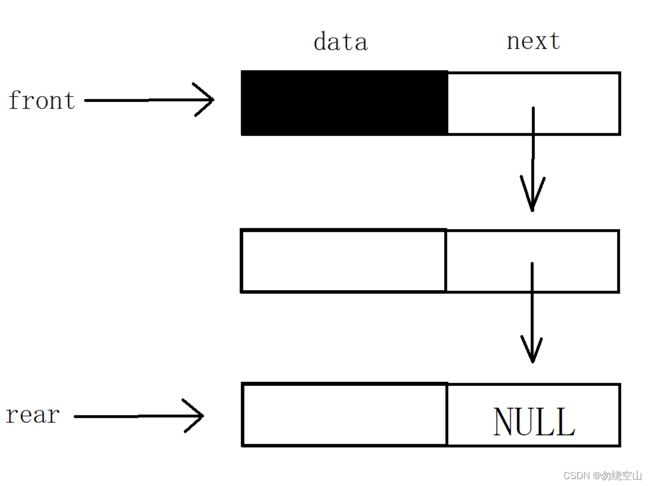
栈的链式存储结构是利用若干结点存储数据元素并组成链表,同时附设top和base指针指示栈顶与栈底的位置。
链栈的逻辑结构示意图:
以下为链栈的相关基本操作:
#include
#include
#include
typedef int ElemType;
typedef struct StackNode
{
ElemType data;
struct StackNode* next;
}StackNode;
typedef struct Stack
{
StackNode* base;
StackNode* top;
}Stack;
//创建结点
StackNode* BuyNewNode()
{
StackNode* newNode = (StackNode*)malloc(sizeof(StackNode));
if (NULL == newNode)
{
printf("空间申请失败\n");
exit(0);
}
newNode->next = NULL;
return newNode;
}
// 初始化栈
void StackInit(Stack* ps)
{
ps->base = BuyNewNode();
ps->top = ps->base;
}
// 入栈
void StackPush(Stack* ps, ElemType data)
{
assert(ps);
StackNode* newNode = BuyNewNode();
newNode->data = data;
newNode->next = ps->top->next;
ps->top = BuyNewNode();
ps->top->next = newNode;
}
// 出栈
void StackPop(Stack* ps)
{
assert(ps);
if (ps->top == ps->base)
{
printf("现在栈中无元素\n");
return;
}
StackNode* temp = ps->top->next;
ps->top->next = temp->next;
free(temp);
temp = NULL;
}
// 获取栈顶元素
ElemType StackTop(Stack* ps)
{
return ps->top->next->data;
}
// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
int count = 0;
StackNode* temp = ps->top->next;
while (temp != NULL)
{
count++;
temp = temp->next;
}
return count;
}
// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
int StackEmpty(Stack* ps)
{
return ps->top == ps->base ? 1 : 0;
}
// 销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
while (ps->top)
{
StackNode* temp = ps->top;
ps->top = temp->next;
free(temp);
}
free(ps->base);
ps->base = NULL;
ps->top = NULL;
} 3.栈与递归的实现
1.递归的简单描述
栈的一个重要应用是在程序设计语言中实现递归。一个直接调用自己或通过一系列的调用语言间接地调用自己地函数,称之为递归函数。
递归是在程序设计中一个强有力地工具。第一,存在许多数学函数是递归定义的,如阶乘函数,斐波那契数列等;第二,有的数据结构,如二叉树,广义表等,他们地结构本身固有递归特性,故他们地操作可递归地描述;第三,某类型的问题,虽然问题本身并没有明显的递归结构,但采用递归求解比迭代求解更方便,如汉诺塔问题。
2.递归过程及与栈的关联
当在一个函数运行期间调用另一个函数时,在运行被调函数之前,系统需要完成三件事:
1.将所有的实参,返回地址等信息传递给被调用函数保存;
2.为被调用函数的局部变量分配存储空间;
3.将控制转移到被调函数的入口。
而从被调函数返回调用函数之前,系统同样完成三项工作:
1.保存被调函数的计算结果;
2.释放被调用函数的数据区;
3.依照被调用函数保存的返回地址将控制转移到调用函数。
多个函数嵌套调用时,按照“后调用先返回”的原则,调用与被调用函数之间的信息传递与控制转移都需要通过栈来实现。
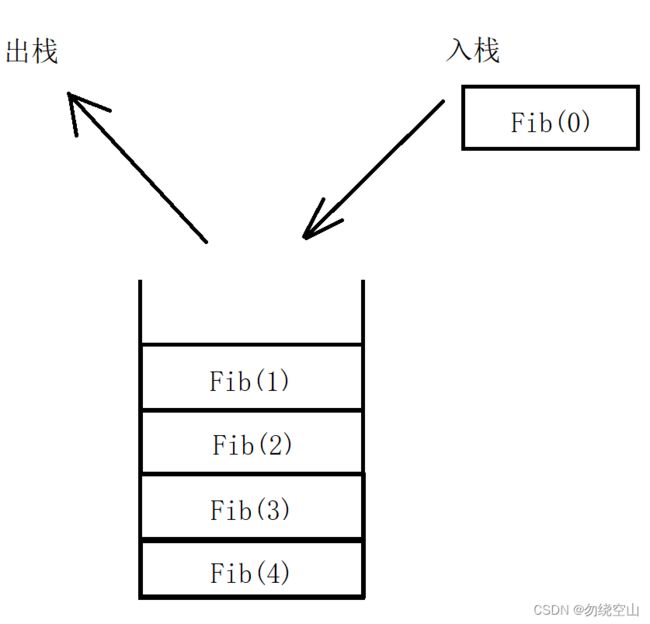
系统将整个程序运行过程中所需的数据空间安排在一个栈中,即“递归工作栈”,每当调用一个函数时,就在栈顶给他分配一个存储区,将当前层递归所需信息构成一个“工作记录”,其中包含调用函数的所有实参,局部变量以及返回地址,将该条工作记录压入栈顶;每当一个函数退出时,就释放他的存储区,从栈顶弹出一个工作记录。当前运行的程序的数据区必须在栈顶。
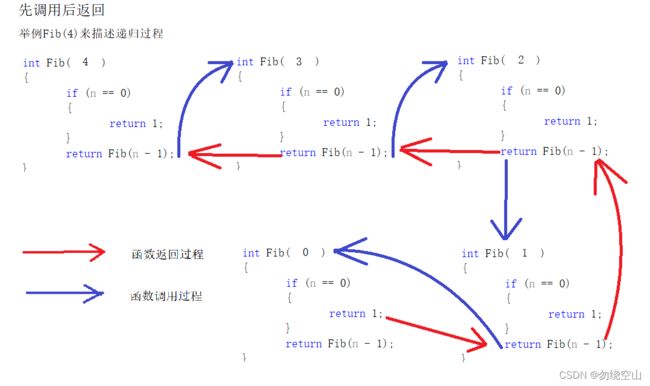
3.递归过程示意图
为了更加具体地描述递归过程及递归过程中栈地应用,方便读者理解,这里给出一个具体递归函数,通过具体案例描述递归过程:
int Fib(int n)
{
if (n == 0)
{
return 1;
}
return Fib(n - 1);
}递归实现过程:
上述递归函数的函数调用栈示意图:
二.队列
1.队列的定义
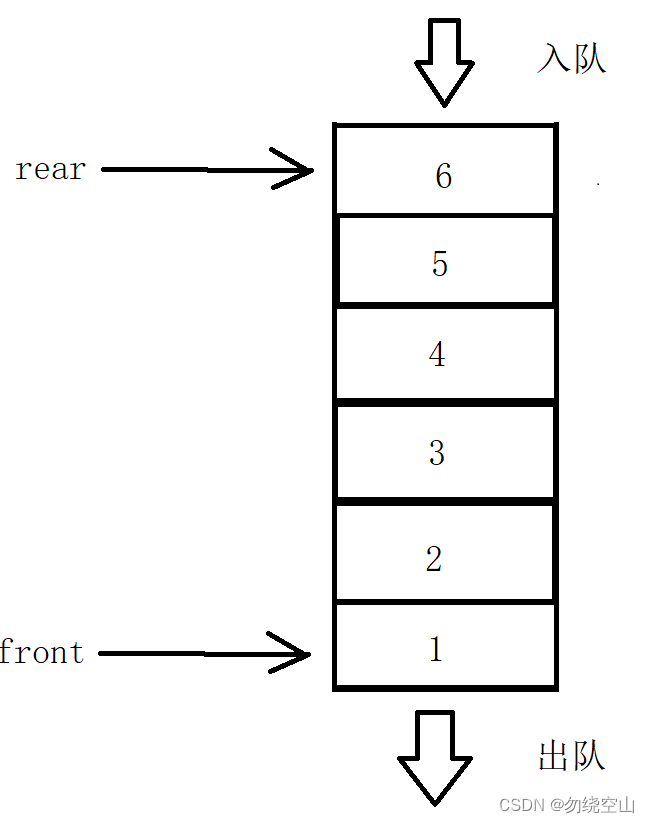
队列是一种先进先出的线性表。它只允许在表的一端进行插入,而在另一端删除元素。在队列中允许插入的一端叫做队尾,允许删除的一端则称为队头。
队列的逻辑示意图:
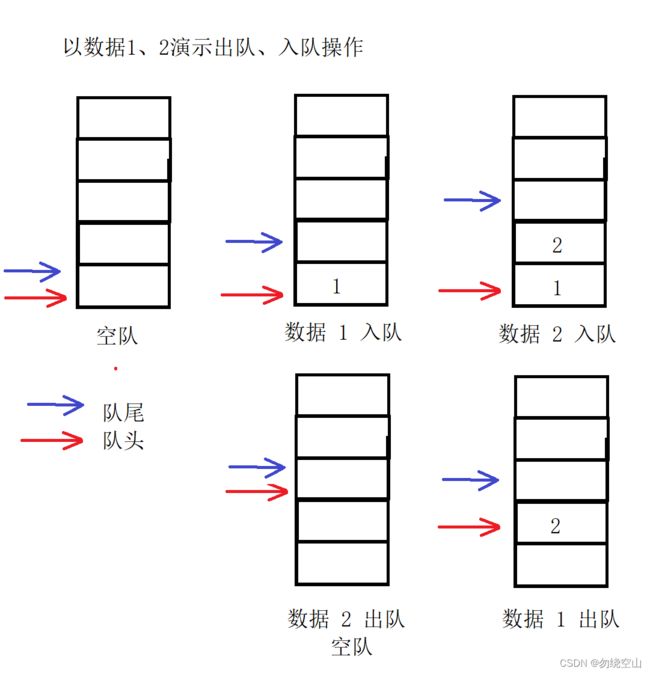
队列的出队、入队操作示意图:(此处只做逻辑解释,不涉及具体存储结构)
2.队列的分类与基本操作
和线性表类似,队列根据存储结构的不同可以分为两类:顺序队列与链式队列。
1.顺序队列
由于顺序队列采用一组地址空间连续的存储空间依次存放队列中的数据元素,在多次出队、入队操作中可能会造成假溢出的现象,使得存储空间利用率不高,为解决假溢出的现象,大佬们引入了循环队列的概念,由于假溢出现象的存在,使得单一线性存储结构不适用于队列,所以此处不多阐述顺序队,详情在下文循环队列中解决。
2.链队列
用链表表示的队列称为链队列。一个链队列需要两个分别指示队头与队尾的指针才能唯一确定。
给出链队列的逻辑示意图:
以下为链队列的相关基本操作:
1.方法一:实现带有头结点的链队列
#include
#include
#include
//定义队列的结构体
typedef int ElemType;
typedef struct QueueNode
{
ElemType data;
struct QueueNode* next;
}QueueNode;
typedef struct Queue
{
QueueNode* front;
QueueNode* rear;
}Queue;
//创建队列的结点
QueueNode* BuyNewNode(ElemType e)
{
QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
if (NULL == newNode)
{
printf("空间申请失败\n");
system("pause");
return;
}
newNode->next = NULL;
newNode->data = e;
return newNode;
}
// 初始化队列
void QueueInit(Queue* q)
{
//定义具有头结点的队列
q->front = (QueueNode*)malloc(sizeof(QueueNode));
if (NULL == q->front)
{
printf("空间申请失败\n");
system("pause");
return;
}
q->front->next = NULL;
q->rear = q->front;
}
// 队尾入队列
void QueuePush(Queue* q, ElemType data)
{
assert(q);
QueueNode* newNode = BuyNewNode(data);
q->rear->next = newNode;
q->rear = newNode;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
if (q->rear == q->front) //当前队列无元素
{
printf("当前队列中为空\n");
return;
}
else if (q->front->next == q->rear) //当前队列仅有一个元素
{
QueueNode* newNode = q->rear;
q->front->next = NULL;
q->rear = q->front;
free(newNode);
newNode = NULL;
}
else //当前队列有多个元素
{
QueueNode* newNode = q->front->next;
q->front->next = newNode->next;
free(newNode);
newNode = NULL;
}
}
// 获取队列头部元素
ElemType QueueFront(Queue* q)
{
assert(q);
if (q->rear == q->front) //当前队列无元素
{
printf("当前队列中为空\n");
return;
}
return q->front->next->data;
}
// 获取队列队尾元素
ElemType QueueBack(Queue* q)
{
assert(q);
if (q->rear == q->front) //当前队列无元素
{
printf("当前队列中为空\n");
return;
}
return q->rear->data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
if (q->rear == q->front) //当前队列无元素
{
printf("当前队列中为空\n");
return;
}
int count = 0;
QueueNode* cur = q->front->next;
while (cur)
{
count++;
cur = cur->next;
}
return count;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
return q->front == q->rear;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
if (QueueEmpty(q))
{
free(q->front);
q->front = NULL;
q->rear = NULL;
}
else{
QueueNode* cur = q->front->next;
while (cur)
{
QueueNode* temp = cur->next;
free(cur);
cur = temp;
}
free(q->front);
q->front = NULL;
q->rear = NULL;
}
} 2.方法二:实现不带头结点的链队列
#include
#include
#include
//定义队列的结构体
typedef int ElemType;
typedef struct QueueNode
{
ElemType data;
struct QueueNode* next;
}QueueNode;
typedef struct Queue
{
QueueNode* front;
QueueNode* rear;
}Queue;
//创建队列的结点
QueueNode* BuyNewNode(ElemType e)
{
QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
if (NULL == newNode)
{
printf("空间申请失败\n");
system("pause");
return;
}
newNode->next = NULL;
newNode->data = e;
return newNode;
}
// 初始化队列
void QueueInit(Queue* q)
{
q->front = NULL;
q->rear = q->front;
}
// 队尾入队列
void QueuePush(Queue* q, ElemType data)
{
assert(q);
QueueNode* newNode = BuyNewNode(data);
if (q->front == NULL) //此时队列为空
{
q->front = q->rear = newNode;
}
{
q->rear->next = newNode;
q->rear = newNode;
}
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
if (q->front == NULL) //当前队列无元素
{
printf("当前队列中为空\n");
return;
}
else if (q->front == q->rear) //当前队列仅有一个元素
{
QueueNode* newNode = q->rear;
q->front = NULL;
q->rear = q->front;
free(newNode);
newNode = NULL;
}
else //当前队列有多个元素
{
QueueNode* newNode = q->front;
q->front = newNode->next;
free(newNode);
newNode = NULL;
}
}
// 获取队列头部元素
ElemType QueueFront(Queue* q)
{
assert(q);
if (NULL == q->front) //当前队列无元素
{
printf("当前队列中为空\n");
return;
}
return q->front->data;
}
// 获取队列队尾元素
ElemType QueueBack(Queue* q)
{
assert(q);
if (NULL == q->front) //当前队列无元素
{
printf("当前队列中为空\n");
return;
}
return q->rear->data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
if (NULL == q->front) //当前队列无元素
{
printf("当前队列中为空\n");
return;
}
int count = 0;
QueueNode* cur = q->front;
while (cur)
{
count++;
cur = cur->next;
}
return count;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
return q->front == NULL;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
if (QueueEmpty(q))
{
free(q->front);
q->front = NULL;
q->rear = NULL;
}
else{
QueueNode* cur = q->front;
while (cur)
{
QueueNode* temp = cur->next;
free(cur);
cur = temp;
}
q->front = NULL;
q->rear = NULL;
}
} 3.循环队列
1.假溢出
队列由于受到“队尾入队,队头出队”这种操作的影响,会在某些状态下不可在插入新的队尾元素,否则会出现溢出现象,即因数组越界而导致程序的非法操作错误。但事实上,此时队列的实际可用空间并未占满,所以这种现象称为假溢出。
示意图:
2.循环队列
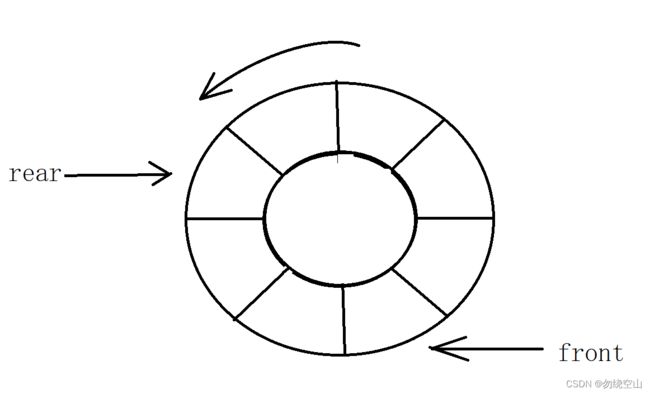
为解决“假溢出”问题,大佬们提出了循环队列,即将顺序队列在逻辑上抽象为一个环状的空间,称为循环队列。
在循环队列中,头、尾指针以及队列元素之间的关系不变,头、尾指针“依环状增1”的操作可通过“模”运算来实现,通过取模,头、尾指针可以在顺序空间内以头尾衔接的方式“循环”移动。
循环队列的判空、判满方法通常有以下两种处理方法:
(1)少使用一个元素空间,即队列大小为m时,有m-1个元素即认为队满,判空条件不变;
队空条件:front == rear
队满条件:(rear+1)%size = front
(2) 另设一个标志位来区别是“空”还是“满”。
3.循环队列相关操作实现:
1.方法 1 :少使用一个存储空间
#include
#include
#include
#define Queue_Init_Size 10
//设计循环队列结构体
typedef int ElemType;
typedef struct Queue
{
ElemType* data;
int front; //队头元素的下标
int rear; //队尾元素的下标
}Queue;
// 初始化队列
void QueueInit(Queue* q)
{
q->data = (ElemType*)malloc(sizeof(ElemType) * Queue_Init_Size);
if (NULL == q->data)
{
printf("空间申请失败\n");
system("pause");
exit(0);
}
q->front = 0;
q->rear = 0;
}
// 队尾入队列
void QueuePush(Queue* q, ElemType data)
{
assert(q);
if ((q->rear + 1) % Queue_Init_Size == q->front)
{
printf("当前队列已满\n");
return;
}
q->data[q->rear] = data;
q->rear = (q->rear + 1) % Queue_Init_Size;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
if (QueueEmpty(q))
{
printf("当前队列为空\n");
return;
}
q->front = (q->front + 1) % Queue_Init_Size;
}
// 获取队列头部元素
ElemType QueueFront(Queue* q)
{
if (!QueueEmpty(q))
{
return q->data[q->front];
}
}
// 获取队列队尾元素
ElemType QueueBack(Queue* q)
{
if (!QueueEmpty(q))
{
return q->data[(q->rear - 1 + Queue_Init_Size) % Queue_Init_Size];
}
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
return (q->rear - q->front + Queue_Init_Size) % Queue_Init_Size;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
return q->front == q->rear;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
if (q->data != NULL)
{
free(q->data);
q->data = NULL;
}
q->front = 0;
q->rear = 0;
} 2.方法 2:另设一个标志位
#include
#include
#include
#define Max_Size 10
//设计循环队列结构体
typedef int ElemType;
typedef struct QArray
{
ElemType data;
int flag;//标志位 0-表示为非空 1-表示为空
}QArray;
typedef struct Queue
{
QArray* task;
int front;
int rear;
}Queue;
// 初始化队列
void QueueInit(Queue* q)
{
q->task = (QArray*)malloc(sizeof(QArray) * Max_Size);
if (NULL == q->task)
{
printf("空间申请失败\n");
exit(0);
}
for (int i = 0; i < Max_Size; ++i)
{
q->task[i].flag = 1;
}
q->front = 0;
q->rear = 0;
}
// 队尾入队列
void QueuePush(Queue* q, ElemType data)
{
assert(q);
if (q->rear == q->front && q->task[q->rear].flag == 0)
{
printf("当前队列空间已满\n");
return;
}
q->task[q->rear].data = data;
q->task[q->rear].flag = 0;
q->rear = (q->rear + 1) % Max_Size;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
if (QueueEmpty(q))
{
printf("当前队列为空\n");
return;
}
q->task[q->front].flag = 1;
q->front = (q->front + 1) % Max_Size;
}
// 获取队列头部元素
ElemType QueueFront(Queue* q)
{
assert(q);
if (!QueueEmpty(q))
{
return q->task[q->front].data;
}
}
// 获取队列队尾元素
ElemType QueueBack(Queue* q)
{
assert(q);
if (!QueueEmpty(q))
{
return q->task[(q->rear - 1 + Max_Size) % Max_Size].data;
}
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
return q->rear == q->front && q->task[q->rear].flag == 1;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
if (QueueEmpty(q))
{
return 0;
}
else if (q->rear == q->front && q->task[q->rear].flag == 0)
{
return Max_Size;
}
else
{
return (q->rear - q->front + Max_Size) % Max_Size;
}
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
if (NULL != q->task)
{
free(q->task);
q->task = NULL;
}
q->front = 0;
q->rear = 0;
}