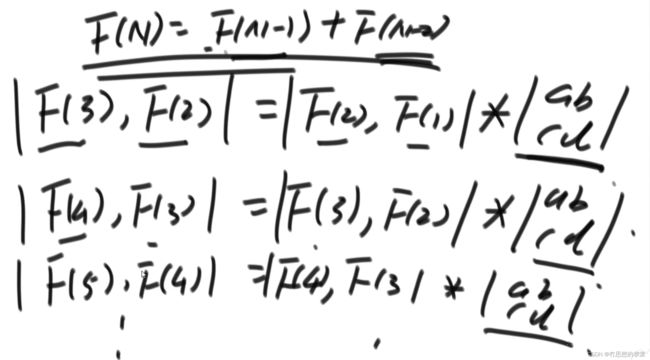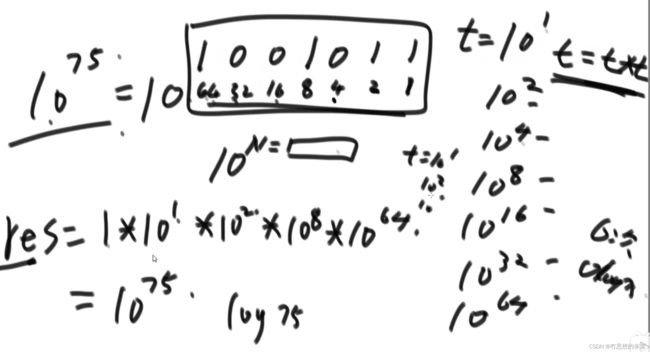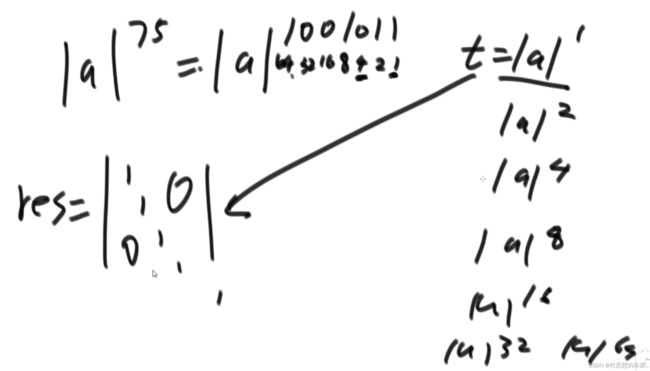左神算法与数据结构——中级提升班-5

中级提升班-5

斐波那契数列套路

• O(N)方法，前两项和为第三项，时间复杂度过高

套路：O（logN），除了初始项，后续每一项都有严格递归式，即递归中不根据条件转移

1. 根据线性代数原理，每个有严格递归形式的递归项，均可表示成以下形式，后向可由前项乘相应的矩阵形式，若后向需要前n项，则矩阵为n阶方阵

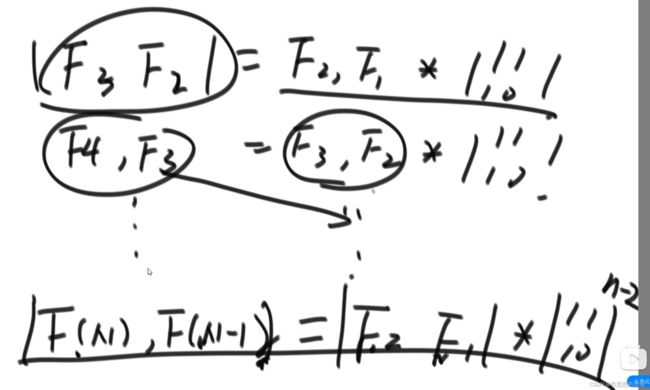
2. 最后一项可以由下图表示，问题转换为求系数矩阵的n次方的最佳方法，可以实现O(logN)

3. 如同求10⁷⁵，将次数75转换成2进制，t表示10¹并不断和自己相乘，得到10¹,10²,10⁴,10⁸···，若进制的第i位为1，则结果乘上t

4. 系数矩阵的求法与求数的n次方相同

vector<vector<int>> matrixMul(vector<vector<int>> a, vector<vector<int>> b) {
    int size = a.size();
    vector<vector<int>> res(size, vector<int>(size));
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            int count = 0;
            for (int k = 0; k < size; k++) {
                count += a[i][k] * b[k][j];
            }
            res[i][j] = count;
        }
    }
    return res;
}

void Fibonacci(int n) {
    vector<vector<int>> t = { {1,1}, {1,0} };
    vector<vector<int>> res(2, vector<int>(2));
    for (int i = 0; i < 2; i++) {
        res[i][i] = 1;
    }
    n -= 2;
    for (; n > 0; n >>= 1) {// 次数不断右移
        if ((n & 1) != 0) {
            res = matrixMul(res, t);
        }
        t = matrixMul(t, t);
    }
    cout << res[0][0] + res[1][0] << endl;
}

• 例子：兔子一年生两只，两岁才到达生育年龄，五年寿命（死亡感觉左神讲的有问题，个人感觉应该是F(N) = F(N-1) + 2(F(N-2) - F(N-5))）

题目一 达标01字符串

斐波那契、打表法

字符串只由’0’和’1’两种字符构成，
当字符串长度为1时，所有可能的字符串为"0"、“1”；
当字符串长度为2时，所有可能的字符串为"00"、“01”、“10”、“11”；
当字符串长度为3时，所有可能的字符串为"000"、“001”、“010”、“011”、“100”、
“101”、“110”、“111”
…
如果某一个字符串中，只要是出现’0’的位置，左边就靠着’1’，这样的字符串叫作达
标字符串。
给定一个正数N，返回所有长度为N的字符串中，达标字符串的数量。
比如，N=3，返回3，因为只有"101"、“110”、"111"达标。

• 打表法可以做，略

斐波那契递归的证明：

• F(i)表示，在第i个位置时候，可以随便分配i及其之后的字符，这就需要i - 1位置为1
• 当第i位固定为1之后，剩余i - 1个字符，若后续为1，则可以调用F(i - 1)，若后续为0，则后续的后续只能填1，再条用F(i - 2)，因此为斐波那契数列形式，但初始值有所改变

代码略

题目二 拼三角形

斐波那契数列

在迷迷糊糊的大草原上，小红捡到了n根木棍，第i根木棍的长度为i，
小红现在很开心。想选出其中的三根木棍组成美丽的三角形。
但是小明想捉弄小红，想去掉一些木棍，使得小红任意选三根木棍都不能组成
三角形。
请问小明最少去掉多少根木棍呢？
给定N，返回至少去掉多少根？

解法：最少去掉多少根和最多保留多少根为相同题目。要使其组成不了三角形，将木棍长度从小到大排列，当前位置木棍长度大于等于前两根木棍长度之和。经证明，只需要等于前面两根木棍之和，就无法形成三角形。

• 例如有17跟木棍，答案为去掉开头的1的小于17的斐波那契数之和

题目三 相邻数字乘积4的倍数

分类讨论

给定一个数组arr，如果通过调整可以做到arr中任意两个相邻的数字相乘是4的倍数，
返回true；如果不能返回false

分情况讨论：

• 分成奇数a个，偶数中含有一个2因子b个，含有不止一个2因子（即4的倍数）c个
• 若没有只有一个2因子的，则排序为“奇4奇4奇4奇···”，c >= a - 1
• 若有2因子
• 1. 1个2因子数：2必须与4放在一起，其余“奇4奇4奇4奇···”，c >= a
  2. 不止1个2因子数：也是c >= a

代码创新点 ：验证奇数新方法，注意比较优先级大于位运算

bool isMuti4(vector<int> arr) {
    if (arr.size() < 1) {
        return false;
    }
    int odd = 0;//奇数
    int even2 = 0;// 偶数2的倍数，但仅有一个2
    int even4 = 0;// 偶数4的倍数
    for (int i : arr) {
        if ((i & 1) != 0) { // 验证奇数新方法，注意比较优先级大于位运算
            odd++;
        }
        else {
            if (i % 4 == 0) {
                even4++;
            }
            else {
                even2++;
            }
        }
    }
    int i = 0;
    return even2 > 0 ? (even4 >= odd) : (even4 >= odd) - 1;
}

题目四日常书写

整型数据的越界判断

给定一个字符串，如果该字符串符合人们日常书写一个整数的形式，返回int类
型的这个数；如果不符合或者越界返回-1或者报错。

例如，以下不符合

要求：

1. 数字之外只能有“-”
2. 如果有-，只能在开头出现一次，且后面数字不能是0
3. 若开头为0，后续不得有数字

要点：

• INT32_MIN比INT32_MAX的范围大1，因此需要用负数来进行数据存储
• 如果数据超过负数范围，则越界
• 若数据刚好等于INT32_MIN，且其为正数，说明也越界

bool isValid(string str) {
    if (str[0] != '-' && (str[0] < '0' || str[0] > '9')) {
        return false;
    }
    if (str[0] == '-' && (str.length() == 1 || str[1] == '0')) {
        return false;
    }
    if (str[0] == '0' && str.length() > 1) {
        return false;
    }
    for (char c : str) {
        if (c < '-' || c > '9') {
            return false;
        }
    }
    return true;
}

int ConvertStringToInteger(string str) {
    if (!isValid(str)) {
        cout << "不合法" << endl;
        return -1;
    }
    bool neg = str[0] == '-' ? true : false;
    int minq = INT32_MIN / 10;
    int minr = INT32_MIN % 10;
    int res = 0;
    int cur = 0;
    for (int i = neg ? 1 : 0; i < str.length(); i++) {
        cur = '0' - str[i]; // 由于负数范围比正数范围大，因此利用负数来进行转换
        if (res < minq || (res == minq && cur < minr)) { // 如果接下来res*10或者加上cur后会超过负数最大值，说明越界
            cout << "不合法" << endl;
            return -1;
        }
        res = res * 10 + cur;
    }
    if (neg && res == INT32_MIN) {// 达到2147483648，超过2147483647int类型最大正整数
        cout << "不合法" << endl;
        return -1;
    }
    res = neg ? -res : res;
    cout << res << endl;
    return res;
}

题目六 牛牛春游背包放零食

动态规划、递归

牛牛准备参加学校组织的春游, 出发前牛牛准备往背包里装入一些零食, 牛牛的背包容
量为w。
牛牛家里一共有n袋零食, 第i袋零食体积为v[i]。
牛牛想知道在总体积不超过背包容量的情况下，他一共有多少种零食放法(总体积为0也
算一种放法)。

dp数组中，表示若任意使用[0…i]中的零食，所要达成不超过w重量的个数，由取第i个零食和不取第i个零食组成

// 递归版本
int process1(vector<int> arr, int i, int weight) {
    if (i == arr.size()) {
        return weight >= 0 ? 1 : 0;
    }
    return process1(arr, i + 1, weight) + process1(arr, i + 1, weight - arr[i]);
}

// 动态规划版本
int process2(vector<int> arr, int w) {
    vector<vector<int>> dp(arr.size(), vector<int>(w + 1));
    for (int i = 0; i < dp.size(); i++) {
        dp[i][0] = 1;
    }
    for (int i = 1; i < dp[0].size(); i++) {
        dp[0][i] = i >= arr[0] ? 2 : 1;
    }
    for (int i = 1; i < dp.size(); i++) {
        for (int j = 1; j <= w; j++) {
            dp[i][j] = dp[i - 1][j] + (j - arr[i] >= 0 ? dp[i - 1][j - arr[i]] : 0);
        }
    }
    return dp[arr.size() - 1][w];
}

题目七 找工作

有序表，自定义排序

为了找到自己满意的工作，牛牛收集了每种工作的难度和报酬。牛牛选工作的标准是在难度不超过自身能力
值的情况下，牛牛选择报酬最高的工作。在牛牛选定了自己的工作后，牛牛的小伙伴们来找牛牛帮忙选工作，
牛牛依然使用自己的标准来帮助小伙伴们。牛牛的小伙伴太多了，于是他只好把这个任务交给了你。
class Job {
public int money;// 该工作的报酬
public int hard; // 该工作的难度
public Job(int money, int hard) {
this.money = money;
this.hard = hard;
}
}
给定一个Job类型的数组jobarr，表示所有的工作。给定一个int类型的数组arr，表示所有小伙伴的能力。
返回int类型的数组，表示每一个小伙伴按照牛牛的标准选工作后所能获得的报酬。

• 按照难度进行排序，相同难度按照待遇进行排序，排序完成删除相同难度所有待遇较低的工作，形成有序表，最终查找难度小于等于个人能力的工作，返回其待遇值

class job {
public:
    int money;
    int hard;
    job(int money, int hard) : money(money), hard(hard) {}
};

bool cmp(const job& a, const job& b) {
    if (a.hard != b.hard) {
        return a.hard > b.hard; // 难度低的放前面
    }
    else {
        return a.money < b.money; // 难度相同，报酬高的放前面
    }
}

vector<int> getPaid(vector<job>& jobs, vector<int>& cap) {
    sort(jobs.begin(), jobs.end(), cmp);
    map<int, int>mp; // 有序表，分别代表难度和报酬
    mp.insert({ jobs[0].hard, jobs[0].money });
    job pre = jobs[0];
    for (int i = 1; i < jobs.size(); i++) {// 将难度递增且待遇递增的工作头部放入mp有序表中
        if (jobs[i].hard > pre.hard && jobs[i].money > pre.money) {
            mp.insert({ jobs[i].hard, jobs[i].money });
            pre = jobs[i];
        }
    }
    vector<int> res(cap.size());
    for (int i = 0; i < res.size(); i++) {
        auto iter = mp.lower_bound(cap[i]);
        if (iter != mp.end()) { // 找到了大于等于能力最近的一个工作
            if (iter->first == cap[i]) { // 该工作能力刚刚好相配
                res[i] = iter->second;
            }
            else if (iter != mp.begin()){ // 该工作不是第一个，若是第一个表示所有工作都比他hard，他是废物
                res[i] = (--iter)->second;
            }
        }
    }
    return res;
}