C++---区间DP---棋盘分割（每日一道算法2023.5.2）

注意事项：
涉及到"矩阵/二维前缀和"的一些知识，建议先理解那篇文章。

题目：
将一个 8×8 的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了 (n−1) 次后，连同最后剩下的矩形棋盘共有 n 块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

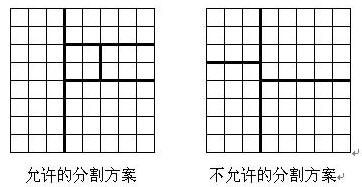
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。
现在需要把棋盘按上述规则分割成 n 块矩形棋盘，并使各矩形棋盘总分的均方差最小。

均方差 ，其中平均值 ，xi 为第 i 块矩形棋盘的总分。

请编程对给出的棋盘及 n，求出均方差的最小值。

输入格式
第 1 行为一个整数 n。
第 2 行至第 9 行每行为 8 个小于 100 的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式
输出最小均方差值（四舍五入精确到小数点后三位）。

数据范围
1

输入:
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

输出：
1.633

#include 
#include 
#include 
#include 
using namespace std;

const int N = 15, M = 9, INF = 1e9;
int n, m = 8;                   //n为最多分割的次数，m固定为棋盘的长宽8*8
int s[M][M];                    //s数组是棋盘的二维前缀和，用来快捷的求出一个区域内的值的总和
double f[M][M][M][M][N];        //f[x1][y1][x2][y2][k]
double X;                       //大写X表示均方差公式中的X拔

double get(int x1, int y1, int x2, int y2) {        //得到(x1, y1)为左上点，(x2, y2)为右下点的区间内的值
    double sum = (s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]) - X;
    return sum*sum / n;
}

double dp(int x1, int y1, int x2, int y2, int k) {  //区间dp
    double &v = f[x1][y1][x2][y2][k];
    if (v >= 0) return v;                       //记忆化搜索，如果当前区间已被计算，直接返回值即可
    if (k == 1) return get(x1, y1, x2, y2);     //如果当前k为1说明是最后一刀，那么就直接返回(x1, y1)(x2, y2)这个区间内的值即可

    //v设为正无穷，因为要取min
    v = INF;
    for (int i = x1; i<x2; i++) {   //枚举x1到x2之间的每一个分割线
        v = min(v, dp(x1, y1, i, y2, k-1) + get(i+1, y1, x2, y2));
        v = min(v, dp(i+1, y1, x2, y2, k-1) + get(x1, y1, i, y2));
    }
    for (int i = y1; i<y2; i++) {   //枚举y1到y2之间的每一个分割线
        v = min(v, dp(x1, y1, x2, i, k-1) + get(x1, i+1, x2, y2));
        v = min(v, dp(x1, i+1, x2, y2, k-1) + get(x1, y1, x2, i));
    }
    return v;
}

int main() {
    //读入，处理二维前缀和
    cin >> n;
    for (int i = 1; i<=m; i++) {
        for (int j = 1; j<=m; j++) {
            cin >> s[i][j];
            s[i][j] = s[i][j] + s[i-1][j] + s[i][j-1] - s[i-1][j-1];
        }
    }

    //f初始化为负数
    memset(f, -1, sizeof f);
    X = (double)s[m][m] / n;
    
    //输出小数点3位，并把算出的最小值开方
    printf("%.3lf", sqrt(dp(1, 1, 8, 8, n)));
    return 0;
}

思路：
思路很简单，其实就是枚举棋盘的所有分割方式，
具体为每次对棋盘进行一次横切或竖切，将棋盘分成两块矩形的子棋盘，
分割完一次后，我们可以选择两个子棋盘中的一个再继续递归操作，
直到分割次数k用完或已经不能再切割为止。

还是经典的y式dp分析法
1.状态表示
f[x1][y1][x2][y2][k]:
以(x1, y1)为左上角，(x2, y2)为右下角的区域，分割k次的所有方案，
属性为Min(最小均方差)。

2.状态计算
枚举所有当前选取的区间的切分可能性：

1.横切，y1到y2间的所有分界线k(切y轴)
上区间值：top = value(x1, y1, x2, k)
下区间值：bot = value(x1, k+1, x2, y2)

2.竖切，x1到x2间的所有分界线k(切x轴)
左区间值：left = value(x1, y1, k, y2)
右区间值：right = value(k+1, y1, x2, y2)

注意这里横切和竖切是并列的关系而不是嵌套，因为横切了就不能竖切，竖切了就不能横切，只能取一种，Min(top, bot, left, right) 即为当前区间最小均方差。

如果有所帮助请给个免费的赞吧~有人看才是支撑我写下去的动力！

声明：
算法思路来源为y总，详细请见https://www.acwing.com/
本文仅用作学习记录和交流