GloVe模型理解
GloVe模型
GloVe(Global Vectors)模型认为语料库中单词出现的统计(共现矩阵)是学习词向量表示的无监督学习算法的重要资料。
问题在于如何基于这些统计生成单词向量表示。
GloVe模型给出了一个答案,它利用了全局(整个)语料库的统计信息。
共现矩阵的例子:
不管语料库有多少篇文档,矩阵的表示考虑的是整个语料库的信息。
为了得到词向量表示,首先定义一些标记符号。记 X X X为单词-单词的词频共现矩阵。
其中的元素 X i j X_{ij} Xij表示单词 j j j 出现在单词 i i i上下文(context)的次数;
并且令 X i = ∑ k X i k X_i = \sum_k X_{ik} Xi=∑kXik为任意单词出现在单词 i i i上下文的次数之和;
令 P i j = P ( j ∣ i ) = X i j X i P_{ij}=P(j|i)=\frac{X_{ij}}{X_i} Pij=P(j∣i)=XiXij为单词 j j j出现在单词 i i i上下文的概率。
通过一个简单的例子来展示是如何从共现概率抽取出某种语义的。考虑两个单词 i i i和 j j j之间的某种特殊兴趣。具体地,假设我们对热力学感兴趣,然后我们令 i = ice i=\text{ice} i=ice(冰)和 j = steam j=\text{steam} j=steam(蒸汽)。这两个单词之间的关系能通过研究它们基于不同单词 k k k得到的共现矩阵概率之比。对于与ice有关但与steam无关的单词,比如说 k = solid k=\text{solid} k=solid(固体),我们期望比值 P i k / P j k P_{ik}/P_{jk} Pik/Pjk会很大;类似地,对于与steam有关但与ice无关的单词,比如 k = gas k=\text{gas} k=gas(气体),该比值应该很小; 而对于那些与两者都相关或都不相关的单词,比如water(水)或fashion(时尚),比值应该接近于 1 1 1。
![]()
上表显示了在大语料库中的这些概率值,以及它们的比值,这些比值肯定了我们的期望。与原始概率相比,比值更能区分相关的单词(比如solid与gas)和不相关的单词(water与fashion),并且也能更好地区分这两个相关的单词。
上面的论述说明词向量学习的好的开端是从共现矩阵概率的比值开始,而不是从共现矩阵概率本身。接下来我们来设计模型,注意,下面很长一部分都是模型的设计阶段,没有严格的论证。
注意到比值 P i k / P j k P_{ik}/P_{jk} Pik/Pjk依赖于三个单词 i , j i,j i,j和 k k k,那么最常见的模型应该是如下形式:
F ( w i , w j , w ∼ k ) = P i k P j k (1) F(w_i,w_j,\overset{\sim}{w}_k) = \frac{P_{ik}}{P_{jk}} \tag{1} F(wi,wj,w∼k)=PjkPik(1)
其中 w ∈ R d w \in R^d w∈Rd是词向量, w ∼ ∈ R d \overset{\sim}{w} \in R^d w∼∈Rd是区分上下文词向量。然后 F F F可能依赖于现在还未指定的参数。
可能的 F F F还是很广,但只要加入一些想法进去我们就能得到唯一的 F F F。
首先,我们希望 F F F能编码信息在词向量空间中表示比值 P i k / P j k P_{ik}/P_{jk} Pik/Pjk。因为向量空间是天然的线性结构,进行向量差计算是很自然的。基于此,我们可以限制函数 F F F只依赖于两个目标词的向量差,将 ( 1 ) (1) (1)式改写为
F ( w i − w j , w ∼ k ) = P i k P j k (2) F(w_i -w_j, \overset{\sim}{w}_k) = \frac{P_{ik}}{P_{jk}} \tag{2} F(wi−wj,w∼k)=PjkPik(2)
现在,我们注意到上式中 F F F的参数是向量,而等式右边是标量。那么 F F F可以由一个复杂的函数,比如,神经网络表示,这样做会我们想要捕获的线性结构冲突。为了避免这个问题,我们让左边也变成标量,可以尝试取这些参数的点积。
F ( ( w i − w j ) T w ∼ k ) = P i k P j k (3) F((w_i-w_j)^T \overset{\sim}{w}_k) = \frac{P_{ik}}{P_{jk}} \tag{3} F((wi−wj)Tw∼k)=PjkPik(3)
这样可以防止 F F F 以不想要的方式混合向量维度。
接下来,注意到单词-单词的共现矩阵是对称的,即改变单词和上下文词位置得到的值是一样的。我们的最终模型应该在这转换下保持不变。要满足这种对称性,需要做以下几步。
第一步,把减法的函数变成函数的除法。
F ( ( w i − w j ) T w ∼ k ) = F ( w i T w ∼ k − w j T w ∼ k ) = F ( w i T w ∼ k ) F ( w j T w ∼ k ) (4) F((w_i-w_j)^T \overset{\sim}{w}_k) = F(w^T_i \overset{\sim}{w}_k - w_j^T \overset{\sim}{w}_k)=\frac{F(w^T_i \overset{\sim}{w}_k)}{F(w^T_j \overset{\sim}{w}_k)} \tag{4} F((wi−wj)Tw∼k)=F(wiTw∼k−wjTw∼k)=F(wjTw∼k)F(wiTw∼k)(4)
联立(3)式,可得
F ( w i T w ∼ k ) = P i k = X i k X i (5) F(w_i^T\overset{\sim}{w}_k) = P_{ik} = \frac{X_{ik}}{X_i} \tag{5} F(wiTw∼k)=Pik=XiXik(5)
要想让 ( 4 ) (4) (4)式成立,可以让 F F F为指数函数,然后取 l o g log log。
w i T w ∼ k = log ( P i k ) = log ( X i k ) − log ( X i ) (6) w_i^T\overset{\sim}{w}_k = \log(P_{ik}) = \log(X_{ik}) - \log(X_i) \tag{6} wiTw∼k=log(Pik)=log(Xik)−log(Xi)(6)
下面,我们注意到等式 ( 6 ) (6) (6) 如 果 没 有 如果没有 如果没有 log ( X i ) \log(X_i) log(Xi) ,就会满足对称的可交换性。然而,该项是与 k k k独立的,所以它可以吸收到 w i w_i wi的偏差 b i b_i bi中。最终,增加 w ∼ k \overset{\sim}{w}_k w∼k的偏差 b ∼ k \overset{\sim}{b}_k b∼k以保证可交换性。得到下面的等式:
w i T w ∼ k + b i + b ∼ k = log ( X i k ) (7) w_i^T\overset{\sim}{w}_k +b_i + \overset{\sim}{b}_k = \log(X_{ik}) \tag{7} wiTw∼k+bi+b∼k=log(Xik)(7)
此时如果把 i i i和 k k k对调,那么上式也成立。等式 ( 7 ) (7) (7)是等式 ( 1 ) (1) (1)的极大简化,但它实际上是有问题的,因为当它的参数为零时,对数就没发散了( log 0 \log 0 log0)。一种解决方案类似拉普拉斯平滑,即增加一个小偏移, log ( X i k ) → log ( 1 + X i k ) \log(X_{ik}) \rightarrow \log(1+X_{ik}) log(Xik)→log(1+Xik),这样既维持了 X X X的稀疏性,又避免对数发散。
这样我们用词向量和偏差项表达了两个词共现的词频的对数。但是该模型的一个缺点是,它将所有的共现概率看成平等的,即使那些很少共现的情况。这些稀有的共现情形可能是噪音或者携带的信息不多。
同时我们希望等式 ( 7 ) (7) (7)两边越接近越好,因此我们利用均方误差(最小二乘法)计算损失,并引入了权重函数 f ( X i j ) f(X_{ij}) f(Xij)。
J = ∑ i , j = 1 V f ( X i j ) ( w i T w ∼ j + b i + b ∼ j − log X i j ) 2 (8) J = \sum^{V}_{i,j=1} f(X_{ij})(w_i^T\overset{\sim}{w}_j +b_i + \overset{\sim}{b}_j - \log X_{ij} )^2 \tag{8} J=i,j=1∑Vf(Xij)(wiTw∼j+bi+b∼j−logXij)2(8)
其中 V V V是词典大小,权重函数应该满足下面条件:
- f ( 0 ) = 0 f(0)=0 f(0)=0,也就是说如果两个词如果没有共同出现过,权重就是0。
- f ( x ) f(x) f(x)应该是非递减函数,所以经常出现的单词权重要大于很少一起出现的单词。
- f ( x ) f(x) f(x)对于较大的 x x x不能取太大的值,所以一些经常出现的词权重不会太大,比如一些停止词。
满足以上条件的函数很多,作者采用了下面的分段函数:
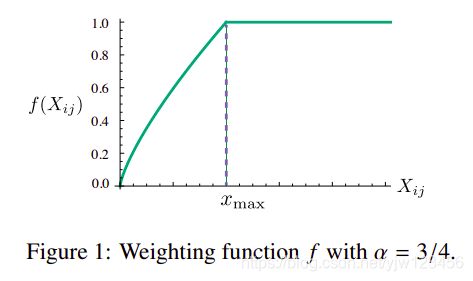
f ( x ) = { ( x / x m a x ) α if x < x m a x 1 otherwise . (9) f(x) = \begin{cases} (x/x_{max})^\alpha & \text{if } x < x_{max} \\ 1 & \text{otherwise } . \end{cases} \tag{9} f(x)={(x/xmax)α1if x<xmaxotherwise .(9)
当 α \alpha α取 3 / 4 3/4 3/4时,函数图像如下:
模型的表现有一点点依赖于 x m a x x_{max} xmax的取值,在作者的实验中都取 x m a x = 100 x_{max}=100 xmax=100。作者发现 α \alpha α取 3 / 4 3/4 3/4要优于取 1 1 1时的线性函数。
该模型生成两组词向量, W W W和 W ∼ \overset{\sim}{W} W∼。当 X X X是对称的时候,这两组词向量是等价的,唯一不同的是它们随机初始化的结果;另一方面,有证据表明,对于某些类型的神经网络,训练神经网络的多个实例,然后组合训练结果能有助于减少过拟合和噪声,通常也会改善结果。因此,作者采用 W + W ∼ W + \overset{\sim}{W} W+W∼之和作为词向量。
参考
- GloVe: Global Vectors for Word Representation