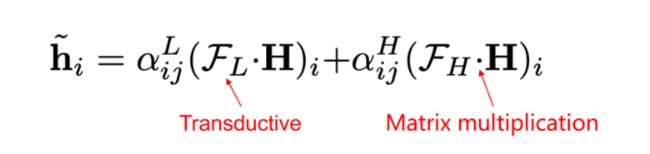【论文笔记】Beyond Low-frequency Information in Graph Convolutional Networks

本文发表在AAAI-21上
论文地址：https://arxiv.org/abs/2101.00797
github：https://github.com/bdy9527/FAGCN

1. Abstract

大多数现有的GNNS 通常利用节点特征的低频信号，这就产生了一个基本的问题：在现实世界的应用中，低频信息都是需要的吗？我们首先进行了一项实验研究，评估了低频信号和高频信号的作用，结果清楚地表明，仅使用低频信号不能在不同的网络中学到有效的节点表示。

我们如何在gnn中自适应地学习更多的低频信息？我们提出了一种具有自门机制的频率自适应图卷积网络(Frequency Adaptation Graph Convolutional Network，FAGCN)，该网络可以在消息传递过程中自适应地集成不同的信号。

为了更深入的理解，我们从理论上分析了低频信号和高频信号在学习节点表示中的作用，这进一步解释了为什么FAGCN可以在不同类型的网络中表现良好。在6个真实网络上的大量实验证明，FAGCN不仅缓解了过度平滑的问题，而且比最新的技术有优势

2. Introduction

• 研究低频和高频信号在gnn中的作用，并验证高频信号对于异配网络是有用的。
• 提出FAGCN，它可以在不知道网络类型的情况下自适应地改变低频和高频信号的比例。
• 理论分析FAGCN是大多数现有gnn的推广，它可以自由地缩短或扩大节点表示之间的距离。
• 做了6个真实网络的实验，FAGCN不仅缓解了over-smoothing的问题，而且比最新的技术有优势

低频和高频信号作用

一般来说，gnn通过聚合来自邻居的信息来更新节点表示，这可以看作是低通滤波器的特殊形式(Wu et al. 2019; Li et al. 2019)。低频信息，是GNN成功的关键。但是，低频信息都是有用的吗？其他信息有什么作用呢？

首先，gnn中的低通滤波器主要保留了节点特征的共性，不可避免地忽略了差异，使得学习到的连通节点表示变得相似。由于低频信息的平滑性，可以很好地用于同配网络（assortative networks），即相似节点倾向于相互连接。然而，现实世界的网络并不总是协调性的，但有时是非协调性的，即来自不同类别的节点往往会相互联系。这里的低频信息不足以支持这种网络中的推理。在这种情况下，高频信息，捕捉节点之间的差异，也许更合适。

其次，当我们总是使用低通滤波器时，节点表示将变得难以区分，导致过平滑。

以低频和高频信号为例，并通过实验来评估它们的作用。结果清楚地表明，它们都有助于学习节点表征。具体地说，我们发现当网络表现出异配性时，高频信号比低频信号表现得更好。这意味着高频信息并非总是无用的，低频信息也并非总是对复杂网络最优的。

一旦识别出gnn中低频信息的弱点，一个自然的问题就是如何在gnn中使用不同频率的信号，同时使gnn适用于不同类型的网络?

要回答这个问题，需要解决两个挑战:

1. 低频和高频信号都是原始特征的部分。传统的滤波器是针对某一特定信号而设计的，不能很好地同时提取不同频率的信号。
2. 即使我们可以提取不同的信息，但是现实世界网络的assortativity 通常是不可知的，变化很大，而且任务与不同信息之间的相关性非常复杂，所以很难决定应该使用哪种信号：原始特征，低频信号，高频信号或它们的组合。

FAGCN怎么设计

• 首先定义了一个增强的低通和高通滤波器，从原始特征中分离低频和高频信号。
• 然后设计一种自门机制（a self-gating mechanism），在不了解网络分类的情况下，自适应地整合低频信号、高频信号和原始特征。

3. An Experimental Investigation

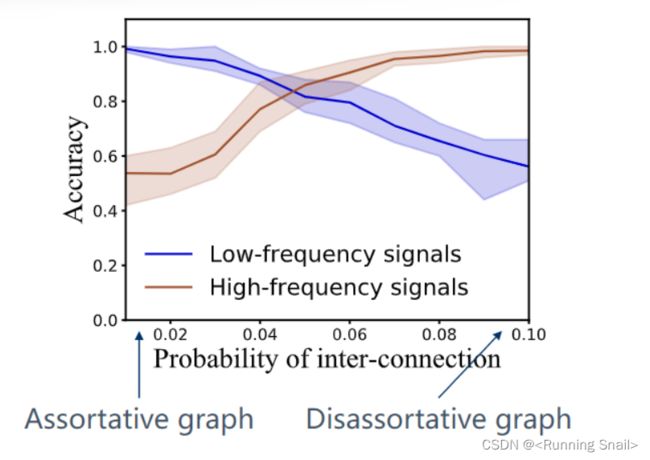
inter-connection：一条边相连的两个节点属于不同类
disassortative graphs：异配图，相邻节点不属于同一类

为了使网络表现出不同的性质，将inter-connection的概率从0增大到0.10，另一个固定为0.5。
在inter-connection很低的时候（图的左侧），网络就会表现出同配性，这种情况下，low-frequency signals会表现得很好。但是随着inter-connection的增大，网络会越来越表现出异配性，这时候high-frequency signals表现更好。

• Low-frequency signals perform better on assortative graphs
• High-frequency signals perform better on disassortative graphs

所以可以得出结论，高、低频信号都有作用

具体怎么实现的？

逐步增加合成网络的异配性，并观察这两种信号的性能如何变化。我们生成一个有200个节点的网络，并将其随机分为2类。对于第一类节点，我们从高斯分布$\mathcal{N}(0.5,1)$中采样一个20维特征向量，而对于第二类节点，高斯分布$\mathcal{N}(-0.5,1)$。

此外，同一类的连接是由$p=0.05$的伯努利分布产生的，两个类之间的连接的概率$q$在0.01到0.1之间。

为什么会出现这种情况？

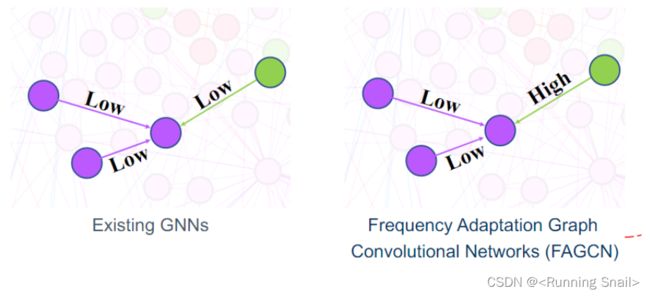
现有的GNN聚合低频信息，但是在聚合低频信息的时候，不会去考虑节点（被聚合的）和自己是不是一类的，都要使表征变得相似，这样就会带来over-smooth

当网络失配时，高频信号的有效性就出现了，但如图1(a)所示，单个滤波器不能在所有情况下都达到最优结果。FAGCN聚合同类型的低频信号，使节点趋同，但又同时不同类型的高频信号，使节点变得不同，以取得比较好的效果

4. Model

4.1 filter定义

首先要做的工作就是寻找filter ，将高、低频的信息进行分离

基于图上的拉普拉斯矩阵设计了两个滤波器：

Low-pass Filter：
$${\mathcal{F}}_L=\epsilon I+D^{-1/2}A{D}^{-1/2}=(\epsilon +1)I-L$$
High-pass Filter：
$${\mathcal{F}}_H=\epsilon I-D^{-1/2}A{D}^{-1/2}=(\epsilon -1)I+L$$

对于信号$x$和$f$：
$$f{\ast }_{G}x=U\left(\left(U^{\top }f\right)\odot \left(U^{\top }x\right)\right)=U{g}_{\theta }{U}^{\top }x$$
如果用${\mathcal{F}}_L$和${\mathcal{F}}_H$代替卷积核$f$：
$$\begin{array}{l}{\mathcal{F}}_L{\ast }_{G}x=U[(\epsilon +1)I-\Lambda ]U^{\top }x={\mathcal{F}}_L\cdot x\\ {\mathcal{F}}_H{\ast }_{G}x=U[(\epsilon -1)I+\Lambda ]U^{\top }x={\mathcal{F}}_H\cdot x\end{array}$$

​ 图2 滤波器的频率响应函数

原来GCN的卷积核$g_{\theta }=I-\Lambda$，现在变为$(\epsilon +1)I-\Lambda$，也可以写成$g_{\theta }\left({\lambda }_i\right)=\epsilon +1-{\lambda }_i$，如图2(a)，但是当${\lambda }_i>1+\epsilon$，$g_{\theta }\left({\lambda }_i\right)<0$，出现 negative amplitude。

所以采用二阶的卷积核$g_{\theta }\left({\lambda }_i\right)=(\epsilon +1-{\lambda }_i{)}^2$，在图2(b)中，${\lambda }_i=0,g_{\theta }\left({\lambda }_i\right)=(\epsilon +1{)}^2>1$，${\lambda }_i=2,g_{\theta }\left({\lambda }_i\right)=(\epsilon +1{)}^2<1$，在二阶的低通滤波器，对低频的信号有比较好的增益，同时对高频信号有比较好的抑制。高通滤波器相反。（思考2）

卷积低频信号${\mathcal{F}}_L\cdot x$的具体含义是空间域内节点特征与邻域特征的和，而高频信号${\mathcal{F}}_H\cdot x$代表空间域内节点特征与邻域特征的差异（解释在模型的${\alpha }_{ij}^G$部分和最后距离分析）

4.2 Aggregation

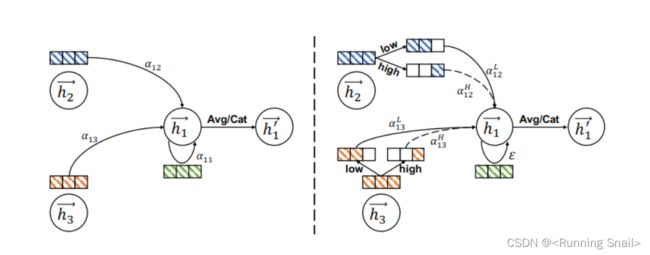
图 3: compare the aggregation process of existing GNNs and FAGCN

左侧是传统的GAT，只需学习一个系数$a_{12}$，对整体的特征做一个聚合；而新模型会先用低通、高通滤波器把特征拆分成低频和高频信息，分别学习一个系数。

4.3 Problems of signal combination

上面是比较初步的版本，有一些缺点：

signal combination：

进行特征提取，比如让低频滤波器与特征矩阵相乘，就可以提取结点的低频信息，然后对于低频信息学习一个系数${\alpha }_{ij}^L$。

1. 因为滤波器是定义在图的拉普拉斯矩阵上，必须要提前知道这个整个图长什么样子，你才可以去是利用这个滤波器。
2. 如果图比较大的话，矩阵乘积的运算是开销比较大的，效率可能也不会太好。

我们在谱域上，虽然解释性比较好，能看到每个节点的低频和高频的权重到底大概是怎么分配的，但是上面的缺点也是不太能接受的，因此，需要一种能自适应地聚合低频和高频信号的有效方法。所以将谱域上的方法转到空域上。

4.4 Spatial vision of FAGCN

为了达到频率适应的目的，一个基本的想法是利用注意机制来学习低频和高频信号的比例

把滤波器全部用矩阵的形式展开：
$${\tilde{\mathbf{h}}}_i={\alpha }_{ij}^L{\left({\mathcal{F}}_L\cdot \mathbf{H}\right)}_i+{\alpha }_{ij}^H{\left({\mathcal{F}}_H\cdot \mathbf{H}\right)}_i=\epsilon {\mathbf{h}}_i+\sum _{j\in {\mathcal{N}}_i}\frac{{\alpha }_{ij}^L-{\alpha }_{ij}^H}{\sqrt{d_i{d}_j}}{\mathbf{h}}_j$$
模型输入的是结点的特征$H=\left\{{\mathbf{h}}_1,{\mathbf{h}}_2,\cdots ,{\mathbf{h}}_N\right\}\in {\mathbb{R}}^{N\times F}$，$F$是结点的维度，${\mathbf{h}}_i$是$i$结点自身特征，${\mathcal{N}}_i$是结点$i$邻居的集合，$d_i$是结点$i$的度，${\alpha }_{ij}^L$和${\alpha }_{ij}^H$代表结点$j$对于结点$i$高低频信息的比例，

整体来看，$\epsilon {\mathbf{h}}_i$是$i$结点自身特征，后面是$i$节点的邻居的一个聚合，标量实际就是聚合时边权重的系数。

4.5 系数${\alpha }_{ij}^G$

两种解释

在谱域下低频、高频信号的和应该是1，${\alpha }_{ij}^L+{\alpha }_{ij}^H=1$，在这里，建模的是低频与高频信号的差值（范围$[-1,1]$）：
$${\alpha }_{ij}^G={\alpha }_{ij}^L-{\alpha }_{ij}^H$$

• ${\alpha }_{ij}^L-{\alpha }_{ij}^H$这个差代表什么？大于0，低频主导，小于0，高频主导。学边上的权重价于低频信号和高频信号的一个比重（减下面的公式），我们之前是要分别去学它的低频线性和高频信号的值到底是多少。但是在这里，就不需要学它们的值到底是多少，只需要去建模他这个差就可以了。
• 另一种是${\alpha }_{ij}^G$表示邻居结点在聚合中的系数。${\alpha }_{ij}^G>0$表示节点特征和邻域特征的和，即$h_i+h_j$，而${\alpha }_{ij}^G<0$表示它们之间的差，即$h_i-h_j$（正如模型刚开始分析的）。此外，当${\alpha }_{ij}^G\approx 0$时，邻居的贡献几乎为0，此时原始特征将占据节点表示的主导地位。

学习系数${\alpha }_{ij}^G$


我们需要考虑节点本身及其邻居的特征。因此，提出了一种自门机制
$${\alpha }_{ij}^G=\tanh \left({\mathbf{g}}^{\top }\left[{\mathbf{h}}_i\Vert {\mathbf{h}}_j\right]\right)$$
类似于GAT，$\mathrm{g}\in {\mathbb{R}}^{2F}$看作共享卷积核，但是没有用Softmax，而是用tanh去激活，把值限制在[-1,1]之间（其实GAT用Softmax也说明了是一种低通滤波器）

4.6 模型整体框架

我们首先使用多层感知器(MLP)对原始特征应用非线性变换。然后我们通过方程6传播这些表示。FAGCN的数学表达式定义为:

Feature transformation 对原始特征做特征变换：
$${\mathbf{h}}_i^{(0)}=\varphi \left({\mathbf{W}}_1{\mathbf{h}}_i\right)\in {\mathbb{R}}^{F^{\prime }\times 1}$$
Propagation （每次都把第一层特征加进来）
$${\mathbf{h}}_i^{(l)}=\epsilon {\mathbf{h}}_i^{(0)}+\sum _{j\in {\mathcal{N}}_i}\frac{{\alpha }_{ij}^G}{\sqrt{d_i{d}_j}}{\mathbf{h}}_j^{(l-1)}\in {\mathbb{R}}^{F^{\prime }\times 1}$$
Classification
$${\mathbf{h}}_{\text{out }}={\mathbf{W}}_2{\mathbf{h}}_i^{(L)}\in {\mathbb{R}}^{K\times 1}$$
${\mathbf{W}}_1\in {\mathbb{R}}^{F\times F^{\prime }}$和${\mathbf{W}}_2\in {\mathbb{R}}^{F\times K}$是权重矩阵，$\varphi$是激活函数，$F^{\prime }$是隐藏层的维数，$l$表示层数(1到L层)

FAGCN的表达能力

为什么低通滤波会让表征相似，高通滤波会让表征不同？

假设Raw feature
$$\mathcal{D}={\Vert {\mathbf{h}}_u-{\mathbf{h}}_v\Vert }_2$$
$h_u,h_v$是节点$u,v$没经过滤波的原始特征，二范数表示距离

Low/High frequency：
$$\begin{gathered} {\mathcal{D}}_L={\Vert \left(\epsilon {\mathbf{h}}_u+{\mathbf{h}}_v\right)-\left(\epsilon {\mathbf{h}}_v+{\mathbf{h}}_u\right)\Vert }_2=|1-\epsilon |\mathcal{D} \\ {\mathcal{D}}_H={\Vert \left(\epsilon {\mathbf{h}}_u-{\mathbf{h}}_v\right)-\left(\epsilon {\mathbf{h}}_v-{\mathbf{h}}_u\right)\Vert }_2=|1+\epsilon |\mathcal{D} \end{gathered}$$
低通滤波用正权重（正权重会让低频信号做主导），让$u,v$聚合后各自得到新的表征，此时再算距离就变成$|1-\epsilon |\mathcal{D}$，这个值一定会小于$\mathcal{D}$，也就是说，低频滤波器表征的距离一定比原始的小。

高通滤波器同理，一定会比原来的距离大。

这就证明了，低通滤波让表征变相似，高通滤波让表征有判别性。

（这里再看作者的视频）

实验