文献阅读笔记--GAN--Generative Adversarial NetworkGAN的原始论文-组会讲解
Generative Adversarial Network
作者:Ian Goodfellow
时间:2014年
会议:NIPS 2014
论文地址Arxiv:https://arxiv.org/abs/1406.2661
Basic idea of GAN
生成对抗网络
GAN 主要包括了两个部分,即生成器 generator 与判别器 discriminator。
- 生成器主要用来学习真实图像分布从而让自身生成的图像更加真实,以骗过判别器。
- 判别器则需要对接收的图片进行真假判别。
在整个过程中,生成器努力地让生成的图像更加真实,而判别器则努力地去识别出图像的真假,这个过程相当于一个二人博弈。
随着时间的推移,生成器和判别器在不断地进行对抗,最终两个网络达到了一个动态均衡:生成器生成的图像接近于真实图像分布,而判别器识别不出真假图像,对于给定图像的预测为真的概率基本接近 0.5(相当于随机猜测类别)
公式和原理
目标函数和最大最小
目标函数
从他的framework 我们可以得到GAN的基本思路,一个生成器一个判别器,尝试从中找到最优解(平衡点)
然后,自然想到如何把这个思想转变成真正的模型。
论文中通过给出目标函数和训练过程来描述这个事情,文章中给出了目标函数:
![]()
思考如何得到目标函数:
首先我们有一些定义
data→真实数据(groundtruth)
pdata→真实数据的分布
z→噪音(输入数据)
pz→原始噪音的分布
pg→经过生成器后的数据分布
G()→生成映射函数
D()→判别映射函数
G 是生成器,结构为一个多层感知机,参数为 θg,G(z;θg) 为生成映射函数,将噪音 z 映射到新的数据空间。
D 是判别器,也是一个多层感知机,参数为 θd,D(x;θd) 输出为一个标量,表示 x 来自真实数据data而不是生成数据的概率。
E ( . ) E(.) E(.) 表示 标签为正类时的期望函数的log 损失函数。
E ( p ∣ y ) = − 1 N ∑ i = 1 N ( y i ( log p i ) + ( 1 − y i ) ( 1 − p i ) ) E(p \mid y)=\frac{-1}{N} \sum_{i=1}^{N}\left(y_{i}\left(\log p_{i}\right)+\left(1-y_{i}\right)\left(1-p_{i}\right)\right) E(p∣y)=N−1i=1∑N(yi(logpi)+(1−yi)(1−pi))
定义最优化问题的方法由两部分组成。首先我们需要定义一个判别器 D 以判别样本是不是从 P data ( x ) P_{\text {data }}(x) Pdata (x) 分布中 取出来的, 因此有:
E x ∼ p data ( x ) log ( D ( x ) ) E_{x \sim p_{\text {data }}(x)} \log (D(x)) Ex∼pdata (x)log(D(x))
其中 E 指代取期望。这一项是根据「正类」 \quad (即辨别出 x \mathrm{x} x 属于真实数据 data ) ) ) 的对数损失函数而构建的。最 大化这一项相当于令判别器 D 在 x \mathrm{x} x 服从于 data 的概率密度时能准确地预测 D ( x ) = 1 \mathrm{D}(\mathrm{x})=1 D(x)=1, 即:
D ( x ) = 1 when x ∼ p data ( x ) D(x)=1 \text { when } x \sim p_{\text {data }}(x) D(x)=1 when x∼pdata (x)
另外一项是企图欺骗判别器的生成器 G。该项根据「负类」的对数损失函数而构建, 即:
E z ∼ p z ( z ) log ( 1 − D ( G ( z ) ) ) E_{z \sim p_{z}(z)} \log (1-D(G(z))) Ez∼pz(z)log(1−D(G(z)))
(上述概念中涉及一个模型认知问题:整个GAN看来是一个无监督的问题,分开来看,D部分其实是一个二分类有监督问题。)
分别 得到 鉴别器和生成器的最优表达式之后,我们可以定义目标函数为:
![]()
对于 D 而言要尽量使公式最大化 (识别能力强),而对于 G 又想使之最小 (生成的数据接近实际数据) 。整 个训练是一个迭代过程。其实极小极大化博亦可以分开理解,即在给定 G 的情况下先最大化 V ( D , G ) V(D, G) V(D,G) 而取 D,然后固定 D, 并最小化 V ( D , G ) V(D, G) V(D,G) 而得到 G。其中, 给定 G, 最大化 V ( D , G ) V(D, G) V(D,G) 评估了 P g P_{g} Pg 和 P data P_{\text {data }} Pdata 之间 的差异或距离。(同时也是训练算法的描述)
D G ∗ = arg max D V ( D , G ) D_{G}^{*}=\arg \max _{D} V(D, G) DG∗=argDmaxV(D,G)
最后,我们可以将最优化问题表达为:
G ∗ = argmin G V ( G , D G ∗ ) G^{*}=\operatorname{argmin}_{G} V\left(G, D_{G}^{*}\right) G∗=argminGV(G,DG∗)
最大最小的博弈过程
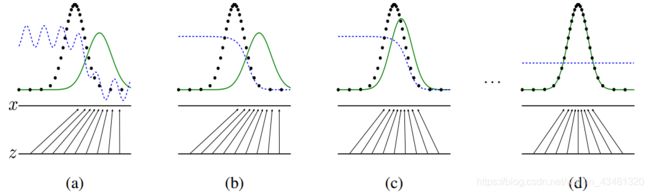
图中,黑色曲线是真实样本的概率分布函数,绿色曲线是虚假样本的概率分布函数,蓝色曲线是判别器D的输出,它的值越大表示这个样本越有可能是真实样本。最下方的平行线是噪声z,它映射到了x。
我们可以看到,一开始, G(z) 和 x 是在同一个特征空间里的,它们分布的差异很大,这时,虽然鉴别真实样本和虚假样本的模型 D 性能也不强,但它很容易就能把两者区分开来,而随着训练的推进,虚假样本的分布逐渐与真实样本重合,D 虽然也在不断更新,但也已经力不从心了。
最后,黑线和绿线最后几乎重合,模型达到了最优状态,这时 D 的输出对于任意样本都是 0.5。
训练方法
![]()

模型按照如图所示的步骤训练。首先固定G,单独训练D,为了让D得到充分训练,有的时候要迭代多次。本论文中每一轮迭代D只训练一次。D训练完毕后,固定D,训练G,如此循环。训练的方式是反向传播算法。
可以注意到,在训练过程中,没有任何求出真实样本的分布或是生成样本的分布的过程。
在每一步的训练中:
- 取 m 个真实数据,使用 G 和 m 组随机数(一般使用服从正态分布的随机数)生成 m 个假数据
- 根据 max 部分的目标更新 D 的参数,提高 D 的分辨能力
- 根据 min 部分的目标更新 G 的参数,使 G 生成的数据更有迷惑性
下面, 我们需要证明:该最优化问题有唯一解 G ∗ , G^{*}, G∗, 并且该唯一解满足 P G = P data P_{G}=P_{\text {data }} PG=Pdata 。
理论部分-全局最优-命题一
命题一证明解析:
- 由目标函数得到$ V(D, G)$的表达式,并把期望改写为积分形式。
(eg:这里是随机变量函数的期望公式,函数为 log D ( x ) \log D(\boldsymbol{x}) logD(x),而 x x x 服从的分布为 p data ( x ) p_{\text {data }}(\boldsymbol{x}) pdata (x) 所以改写为如图形式) - 根据测度论中的 Radon-Nikodym 定理进行变换,得到第二个等号。
(说明:见备注一,备注二,备注三) - 在数据给定, G 给定的前提下, P data ( x ) \quad P_{\text {data }}(x) Pdata (x) 与 P G ( x ) P_{G}(x) PG(x) 都可以看作是常数,我们可以分别用 a , b a, b a,b 来表示他们,这样我们就可以得到如下的式子:

- 在满足定理结论中的条件处,达到了最小,证明了第一个条件得到了,给定G的时候,鉴别器所满足的条件。
当然 GAN 过程的目标是令 P G = P data 。 P_{G}=P_{\text {data } 。} PG=Pdata 。 这对最优的 D 意味着什么呢? 我们可以将这一等式代入 D G ∗ D_{G *} DG∗ 的表达式中:
D G ∗ = p data p data + p G = 1 2 D_{G}^{*}=\frac{p_{\text {data }}}{p_{\text {data }}+p_{G}}=\frac{1}{2} DG∗=pdata +pGpdata =21
这意味着判别器已经完全困惑了,它完全分辨不出 P data P_{\text {data }} Pdata 和 P G P_{G} PG 的区别, 即判断样本来自 P data P_{\text {data }} Pdata 和 P G P_{G} PG 的概率都为 1 2 \frac{1}{2} 21 。基于这一观点, GAN 作者证明了 G 就是极小极大博亦的解。该定理如下:
理论部分-全局最优-定理1
定理一证明解析:
由定理 if an only if:
可以看到这是一个充分必要条件,故需要进行双向证明。
首先我们先从反向逼近并证明 C ( G ) C(G) C(G) 的取值, 然后再利用由反向获得的新知识从正向证明。设 P G = P data P_{G}=P_{\text {data }} PG=Pdata (反向指预先知道最优 条件并做推导),我们可以反向推出
V ( G , D G ∗ ) = ∫ x p data ( x ) log 1 2 + p G ( x ) log ( 1 − 1 2 ) d x V\left(G, D_{G}^{*}\right)=\int_{x} p_{\text {data }}(x) \log \frac{1}{2}+p_{G}(x) \log \left(1-\frac{1}{2}\right) \mathrm{d} x V(G,DG∗)=∫xpdata (x)log21+pG(x)log(1−21)dx
and
V ( G , D G ∗ ) = − log 2 ∫ x p G ( x ) d x − log 2 ∫ x p data ( x ) d x = − 2 log 2 = − log 4 V\left(G, D_{G}^{*}\right)=-\log 2 \int_{x} p_{G}(x) \mathrm{d} x-\log 2 \int_{x} p_{\text {data }}(x) \mathrm{d} x=-2 \log 2=-\log 4 V(G,DG∗)=−log2∫xpG(x)dx−log2∫xpdata (x)dx=−2log2=−log4
该值是全局最小值的候选, 因为它只有在 P G = P data P_{G}=P_{\text {data }} PG=Pdata 的时候才出现。
然后,我们现在需要从正向证明这一个值常常为最小值,也就是同时满足「当」和「仅当」的条件。
现在放弃 P G = P data P_{G}=P_{\text {data }} PG=Pdata 的假设, 对任意一
个 G,我们可以将上一步求出的最优判别器 D ∗ D^{*} D∗ 代入到 C ( G ) = max V ( G , D ) C(G)=\max V(G, D) C(G)=maxV(G,D) 中:
C ( G ) = ∫ x p data ( x ) log ( p data ( x ) p G ( x ) + p data ( x ) ) + p G ( x ) log ( p G ( x ) p G ( x ) + p data ( x ) ) d x C(G)=\int_{x} p_{\text {data }}(x) \log \left(\frac{p_{\text {data }}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right)+p_{G}(x) \log \left(\frac{p_{G}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right) \mathrm{d} x C(G)=∫xpdata (x)log(pG(x)+pdata (x)pdata (x))+pG(x)log(pG(x)+pdata (x)pG(x))dx
(技巧性的一步:因为已知 -log4 为全局最小候选值,所以我们希望构造某个值以使方程式中出现 log2。因此我们可以在每个积分中加上或减去 log2,并乘上概率密度。这是一个十分常见并且不会改变等式的数学证明技巧,因为本质上我们只是在方程加上了 0。)
C ( G ) = ∫ x ( log 2 − log 2 ) p data ( x ) + p data ( x ) log ( p data ( x ) p G ( x ) + p data ( x ) ) + ( log 2 − log 2 ) p G ( x ) + p G ( x ) log ( p G ( x ) p G ( x ) + p data ( x ) ) d x \begin{aligned} C(G) &=\int_{x}(\log 2-\log 2) p_{\text {data }}(x)+p_{\text {data }}(x) \log \left(\frac{p_{\text {data }}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right) \\ &+(\log 2-\log 2) p_{G}(x)+p_{G}(x) \log \left(\frac{p_{G}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right) \mathrm{d} x \end{aligned} C(G)=∫x(log2−log2)pdata (x)+pdata (x)log(pG(x)+pdata (x)pdata (x))+(log2−log2)pG(x)+pG(x)log(pG(x)+pdata (x)pG(x))dx
采用该技巧主要是希望能够构建成含 log2 和 JS 散度的形式, 上式化简后可以得到以下表达式:
C ( G ) = − log 2 ∫ x p G ( x ) + p data ( x ) d x + ∫ x p data ( x ) ( log 2 + log ( p data ( x ) p G ( x ) + p data ( x ) ) ) + p G ( x ) ( log 2 + log ( p G ( x ) p G ( x ) + p data ( x ) ) ) d x \begin{array}{c} C(G)=-\log 2 \int_{x} p_{G}(x)+p_{\text {data }}(x) \mathrm{d} x \\ +\int_{x} p_{\text {data }}(x)\left(\log 2+\log \left(\frac{p_{\text {data }}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right)\right) \\ +p_{G}(x)\left(\log 2+\log \left(\frac{p_{G}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right)\right) \mathrm{d} x \end{array} C(G)=−log2∫xpG(x)+pdata (x)dx+∫xpdata (x)(log2+log(pG(x)+pdata (x)pdata (x)))+pG(x)(log2+log(pG(x)+pdata (x)pG(x)))dx
因为概率密度的定义, P G P_{G} PG 和 P data P_{\text {data }} Pdata 在它们积分域上的积分等于 1 , 即:
− log 2 ∫ x p G ( x ) + p data ( x ) d x = − log 2 ( 1 + 1 ) = − 2 log 2 = − log 4 -\log 2 \int_{x} p_{G}(x)+p_{\text {data }}(x) \mathrm{d} x=-\log 2(1+1)=-2 \log 2=-\log 4 −log2∫xpG(x)+pdata (x)dx=−log2(1+1)=−2log2=−log4
此外,根据对数的定义, 我们有:
log 2 + log ( p data ( x ) p G ( x ) + p data ( x ) ) = log ( 2 p data ( x ) p G ( x ) + p data ( x ) ) = log ( p data ( x ) ( p G ( x ) + p data ( x ) ) / 2 ) \begin{array}{c} \log 2+\log \left(\frac{p_{\text {data }}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right)=\log \left(2 \frac{p_{\text {data }}(x)}{p_{G}(x)+p_{\text {data }}(x)}\right) \\ =\log \left(\frac{p_{\text {data }}(x)}{\left(p_{G}(x)+p_{\text {data }}(x)\right) / 2}\right) \end{array} log2+log(pG(x)+pdata (x)pdata (x))=log(2pG(x)+pdata (x)pdata (x))=log((pG(x)+pdata (x))/2pdata (x))
因此代入该等式, 我们可以写为:
C ( G ) = − log 4 + ∫ x p data ( x ) log ( p data ( x ) ( p G ( x ) + p data ( x ) ) / 2 ) d x + ∫ x p G ( x ) log ( p G ( x ) ( p G ( x ) + p data ( x ) ) / 2 ) d x \begin{aligned} C(G)=&-\log 4+\int_{x} p_{\text {data }}(x) \log \left(\frac{p_{\text {data }}(x)}{\left(p_{G}(x)+p_{\text {data }}(x)\right) / 2}\right) \mathrm{d} x \\ &+\int_{x} p_{G}(x) \log \left(\frac{p_{G}(x)}{\left(p_{G}(x)+p_{\text {data }}(x)\right) / 2}\right) \mathrm{d} x \end{aligned} C(G)=−log4+∫xpdata (x)log((pG(x)+pdata (x))/2pdata (x))dx+∫xpG(x)log((pG(x)+pdata (x))/2pG(x))dx
现在, 如果读者阅读了前文的 KL 散度, 那么我们就会发现每一个积分正好就是它。具体来说:
C ( G ) = − log 4 + K L ( p data ∣ p data + p G 2 ) + K L ( p G ∣ p data + p G 2 ) C(G)=-\log 4+K L\left(p_{\text {data }} \mid \frac{p_{\text {data }}+p_{G}}{2}\right)+K L\left(p_{G} \mid \frac{p_{\text {data }}+p_{G}}{2}\right) C(G)=−log4+KL(pdata ∣2pdata +pG)+KL(pG∣2pdata +pG)
KL散度是非负的, 所以我们马上就能看出来 -log4 为 C ( G ) C(G) C(G) 的全局最小值。 如果我们进一步证明只有一个 G 能达到这一个值, 因为 P G = P data P_{G}=P_{\text {data }} PG=Pdata 将会成为令 C ( G ) = − log 4 C(G)=-\log 4 C(G)=−log4 的
从前文可知 KL 散度是非对称的, 所以 C ( G ) C(G) C(G) 中的 K L ( P data ∥ ( P data + P G ) / 2 ) K L\left(P_{\text {data }} \|\left(P_{\text {data }}+P_{G}\right) / 2\right) KL(Pdata ∥(Pdata +PG)/2) 左右两项是不能交换 的, 但如果同时加上另一项 K L ( P data ∥ ( P data + P G ) / 2 ) K L\left(P_{\text {data }} \|\left(P_{\text {data }}+P_{G}\right) / 2\right) KL(Pdata ∥(Pdata +PG)/2), 它们的和就能变成对称项。这两项 KL 散度 的和即可以表示为 JS 散度(Jenson-Shannon divergence ) :
JSD ( P ∥ Q ) = 1 2 D ( P ∥ M ) + 1 2 D ( Q ∥ M ) M = 1 2 ( P + Q ) \begin{aligned} \operatorname{JSD}(P \| Q)=\frac{1}{2} D(P \| M) &+\frac{1}{2} D(Q \| M) \\ M &=\frac{1}{2}(P+Q) \end{aligned} JSD(P∥Q)=21D(P∥M)M+21D(Q∥M)=21(P+Q)
假设存在两个分布 P 和 Q, 且这两个分布的平均分布 M = ( P + Q ) / 2 , M=(P+Q) / 2, M=(P+Q)/2, 那么这两个分布之间的 JS 散 度为 P 与 M 之间的 KL散度加上 Q 与 M 之间的 KL 散度再除以 2。 JS 散度的取值为 0 到 log2。若两个分布完全没有交集,那么 JS 散度取最大值 log2; 若两个分布完全一 样, 那么 JS 散度取最小值 0。 因此 C ( G ) C(G) C(G) 可以根据 JS 散度的定义改写为:
C ( G ) = − log 4 + 2 ⋅ J S D ( p data ∣ p G ) C(G)=-\log 4+2 \cdot J S D\left(p_{\text {data }} \mid p_{G}\right) C(G)=−log4+2⋅JSD(pdata ∣pG)
这一散度其实就是 Jenson-Shannon 距离度量的平方。根据它的属性: 当 P G = P data P_{G}=P_{\text {data }} PG=Pdata 时, J S D ( P data ( x ) ∥ P G ( x ) ) J S D\left(P_{\text {data }}(x) \| P_{G}(x)\right) JSD(Pdata (x)∥PG(x)) 为 0 。综上所述, 生成分布当且仅当等于真实数据分布式时, 我们可以取得最 优生成器。
(
)
理论部分-算法收敛-命题二
给定足够的训练数据和正确的环境,训练过程将收敛到最优 G
命题2。如果G和D有足够的能力,在算法1的每一步, 让判别器达到给定的最优G,并更新pg以改进标准。。
E x ∼ p data [ log D G ∗ ( x ) ] + E x ∼ p g [ log ( 1 − D G ∗ ( x ) ) ] \mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right] Ex∼pdata [logDG∗(x)]+Ex∼pg[log(1−DG∗(x))]
然后pg收敘到pdata
证明。将V ( G , D ) = U ( p g , D ) (\mathrm{G}, \mathrm{D})=\mathrm{U}(\mathrm{pg}, \mathrm{D}) (G,D)=U(pg,D) 视为上述准则中pg的函数。 \quad 注意U U ( p g , \mathrm{U}(\mathrm{pg}, U(pg, D)在pg中是凸的, 凸函数的上项的子导数 包括函数在最大点处的导数。换句话说, 如果 f ( x ) = sup α ∈ A f α ( x ) f(x)=\sup _{\alpha \in A} f_{\alpha}(x) f(x)=supα∈Afα(x) 并且 f α ( x ) f_{\alpha}(x) fα(x) 对每个 α \alpha α 中的x都是凸的, 如果
G.sup D ⋃ ( P g , D ) 在pg中凸且有唯一全局最优 _{D} \bigcup\left(P_{g}, D\right)_{\text {在pg中凸且有唯一全局最优 }} D⋃(Pg,D)在pg中凸且有唯一全局最优 β = argsup α ∈ A f α ( x ) \beta=\operatorname{argsup}_{\alpha \in A} f_{\alpha}(x) β=argsupα∈Afα(x) 则 α f β ( x ) ∈ α f 。 \alpha f_{\beta}(x) \in \alpha f_{\text {。}} αfβ(x)∈αf。这相当于在给定对应
值的情况下计算pg在最优D处的梯度下降更新, 已在thm1中证明, 因此在pg更新足够小的情况下,pg收敘于 p x , \mathrm{px}, px, 得出证明。
在实践中, 对抗网络通过函数G ( z ; θ g ) (z ; \theta g) (z;θg) 表示有限的pg分布族;而我们优化的是\thetag而不是pg本身。用多层感知器 定义G引入了参数空间中的多个临界点。然而, 多层感知器在实际应用中的优异性能表明, 尽管其缺乏理论保 障,但仍是一种合理的模型。
参考资料
知识补充
极大似然估计
在这里的关键是,引出,生成器生成分布和真实分布差距衡量的思路,但无法计算,所以,GAN解决了这个问题
https://zhuanlan.zhihu.com/p/266677860
我们根本无法算出 生成器的分布
最后包含,生成器的分布是包含一个 G(z)= x的示性函数,而,GAN 正是由这个思路提出了鉴别器的思路,因为鉴别器在鉴别的就是 生成的时候是x(真实的)
https://blog.csdn.net/stalbo/article/details/79283399
KL散度(KL divergence)
这是统计中的一个概念,是衡量两种概率分布的相似程度,其越小,表示两种概率分布越接近。
离散的:
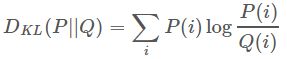
连续的:
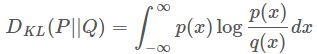
GAN中的应用:
我们想要将一个随机高斯噪声z通过一个生成网络G得到一个和真的数据分布 P data ( x ) P_{\text {data }}(x) Pdata (x) 差不多的生成 分布 P G ( x ; θ ) , P_{G}(x ; \theta), PG(x;θ), 其中的参数 θ \theta θ 是网络的参数决定的,我们希望找到 θ \theta θ 使得 P G ( x ; θ ) P_{G}(x ; \theta) PG(x;θ) 和 P data ( x ) P_{\text {data }}(x) Pdata (x) 尽可能接近。
注意:KL散度不是距离。因此KL散度不具有交换性,所以不能理解为距离的概念,衡量的并不是两分布在空间中的远近,更准确的理解应该是衡量一个分布比另一个分布的信息损失。
JS散度
JS散度用于衡量两种分布之间的差异,它用在生成对抗网络的数学推到上,克服了KL散度不是距离、不对称的缺点
它的定义如下
JSD ( p ∥ q ) = 1 2 D ( p ∥ m ) + 1 2 D ( q ∥ m ) , m = 1 2 ( p + q ) \operatorname{JSD}(\mathrm{p} \| \mathrm{q})=\frac{1}{2} \mathrm{D}(\mathrm{p} \| \mathrm{m})+\frac{1}{2} \mathrm{D}(\mathrm{q} \| \mathrm{m}), \mathrm{m}=\frac{1}{2}(p+q) JSD(p∥q)=21D(p∥m)+21D(q∥m),m=21(p+q)
总结
关于GAN
本质都是,尝试取衡量 真实分布和生成结果的距离或者相似程度,拟合程度。
其实在GAN之前,就已经有Auto-Encoder,VAE这样的方法来使用神经网络做生成式任务了。
GAN的最大的创新就是在于非常精妙地引入了判别器,从样本的维度解决了衡量两个分布差异的问题。
这种生成器和判别器对抗学习的模式,也必将在各种生成式任务中发挥其巨大的威力。
备注
备注一:
在 GAN 原论文中,有一个思想和其它很多方法都不同,即生成器 G 不需要满足可逆条件。Scott Rome 认为这一点非常重要,因为实践中 G 就是不可逆的。而很多证明笔记都忽略了这一点,他们在证明时错误地使用了积分换元公式,而积分换元却又恰好基于 G 的可逆条件。Scott 认为证明只能基于以下等式的成立性:
E z ∼ p z ( z ) log ( 1 − D ( G ( z ) ) ) = E x ∼ p G ( x ) log ( 1 − D ( x ) ) E_{z \sim p_{z}(z)} \log (1-D(G(z)))=E_{x \sim p_{G(x)}} \log (1-D(x)) Ez∼pz(z)log(1−D(G(z)))=Ex∼pG(x)log(1−D(x))
该等式来源于测度论中的 Radon-Nikodym 定理。。 有一些证明过程使用了积分换元公式, 但进行积分换元就必须计算 G ( − 1 ) G^{(-1)} G(−1), 而 G 的逆却并没有假定为存 在。并且在神经网络的实践中,它也并不存在。可能这个方法在机器学习和统计学文献中太常见了, 因 此我们忽略了它。
关于,生成器可逆的问题,思考在备注二。
关于R-N定理的通俗理解,见备注三。
备注二:
根据以下几个观点构成备注二:
- 普通积分还原公式,要求变换的函数 在 [ a , b ] [a, b] [a,b]闭区间上可导等条件。
- 神经网络中,通常不是普通的一元、多元函数,而是矩阵函数。
- 个人认为,矩阵函数想要进行积分还原公式,需要要求系数矩阵可逆。
- 结合备注一的结论,G实际中基本上都是不可逆的。举个例子来说明这个问题,GAN的最简单形式中,生成器使用的只是一个简单的多层感知机(见代码)。
- 同时,多层感知机是一个线性层+激活函数
- 理论上,线性层+单射的激活函数,就可逆。
- 但实际情况中,神经网络对应的矩阵(本质就是一个矩阵相乘)不是方阵,所以,实际中,这个过程不可逆。
- 是奇异阵或者是方阵的时候,无解或者多解。这都是不可逆的。
- 举一个简单的例子帮助理解:一个行向量和一个列向量相乘得到一个值。我们怎么可能在知道这个值和网络参数的时候得到 输入值呢?
- 故其实,大多数生成器,包括普通的多层感知机都是不可逆。因为这实在是一个太基本的东西,反而很少见人讨论。
(ack-天天)
备注三:
学习DL中,我们无需懂得在测度论中如何证明R-N定理(多种证明方法)
可以从直觉上明白一个事情。
R-N定理是一个广义的积分换元定理,无视了可逆条件
顺便可以加深一个概念,GAN积分等式中的,
p G ( x ) p_{G}(x) pG(x)和 p ( z ) p(z) p(z) 包括 x,z 就是一种测度。
该定理支持了在满足一定条件下,测度之间变换。


理论部分参考资料:
- GAN - Intuitive Approach to Mathematics
- https://blog.csdn.net/stalbo/article/details/79283399
代码
import argparse
import os
import numpy as np
import math
import torchvision.transforms as transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch
os.makedirs("images", exist_ok=True)
parser = argparse.ArgumentParser()
parser.add_argument("--n_epochs", type=int, default=200, help="number of epochs of training")
parser.add_argument("--batch_size", type=int, default=64, help="size of the batches")
parser.add_argument("--lr", type=float, default=0.0002, help="adam: learning rate")
parser.add_argument("--b1", type=float, default=0.5, help="adam: decay of first order momentum of gradient")
parser.add_argument("--b2", type=float, default=0.999, help="adam: decay of first order momentum of gradient")
parser.add_argument("--n_cpu", type=int, default=8, help="number of cpu threads to use during batch generation")
parser.add_argument("--latent_dim", type=int, default=100, help="dimensionality of the latent space")
parser.add_argument("--img_size", type=int, default=28, help="size of each image dimension")
parser.add_argument("--channels", type=int, default=1, help="number of image channels")
parser.add_argument("--sample_interval", type=int, default=400, help="interval betwen image samples")
opt = parser.parse_args()
print(opt)
img_shape = (opt.channels, opt.img_size, opt.img_size)
cuda = True if torch.cuda.is_available() else False
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
def block(in_feat, out_feat, normalize=True):
layers = [nn.Linear(in_feat, out_feat)]
if normalize:
layers.append(nn.BatchNorm1d(out_feat, 0.8))
layers.append(nn.LeakyReLU(0.2, inplace=True))
return layers
self.model = nn.Sequential(
*block(opt.latent_dim, 128, normalize=False),
*block(128, 256),
*block(256, 512),
*block(512, 1024),
nn.Linear(1024, int(np.prod(img_shape))),
nn.Tanh()
)
def forward(self, z):
img = self.model(z)
img = img.view(img.size(0), *img_shape)
return img
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.model = nn.Sequential(
nn.Linear(int(np.prod(img_shape)), 512),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(512, 256),
nn.LeakyReLU(0.2, inplace=True),
nn.Linear(256, 1),
nn.Sigmoid(),
)
def forward(self, img):
img_flat = img.view(img.size(0), -1)
validity = self.model(img_flat)
return validity
# Loss function
adversarial_loss = torch.nn.BCELoss()
# Initialize generator and discriminator
generator = Generator()
discriminator = Discriminator()
if cuda:
generator.cuda()
discriminator.cuda()
adversarial_loss.cuda()
# Configure data loader
os.makedirs("../../data/mnist", exist_ok=True)
dataloader = torch.utils.data.DataLoader(
datasets.MNIST(
"../../data/mnist",
train=True,
download=True,
transform=transforms.Compose(
[transforms.Resize(opt.img_size), transforms.ToTensor(), transforms.Normalize([0.5], [0.5])]
),
),
batch_size=opt.batch_size,
shuffle=True,
)
# Optimizers
optimizer_G = torch.optim.Adam(generator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
optimizer_D = torch.optim.Adam(discriminator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
# ----------
# Training
# ----------
for epoch in range(opt.n_epochs):
for i, (imgs, _) in enumerate(dataloader):
# Adversarial ground truths
valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)
# Configure input
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train Generator
# -----------------
optimizer_G.zero_grad()
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# Generate a batch of images
gen_imgs = generator(z)
# Loss measures generator's ability to fool the discriminator
g_loss = adversarial_loss(discriminator(gen_imgs), valid)
g_loss.backward()
optimizer_G.step()
# ---------------------
# Train Discriminator
# ---------------------
optimizer_D.zero_grad()
# Measure discriminator's ability to classify real from generated samples
real_loss = adversarial_loss(discriminator(real_imgs), valid)
fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), fake)
d_loss = (real_loss + fake_loss) / 2
d_loss.backward()
optimizer_D.step()
print(
"[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]"
% (epoch, opt.n_epochs, i, len(dataloader), d_loss.item(), g_loss.item())
)
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)
在这个实现中需要注意的一点是,原论文中 G 的训练是希望减小 log(1-D(G(z)),而代码中是使用二值交叉熵BCE(G(z), 1),即希望提高-log(D(G(x))),虽然都是希望让 D(G(x)) 趋近于1 ,但数值上还是有细微的不同。
代码部分参考资料
代码参考资料