KMP算法深度解析

摘要：KMP算法是字符串匹配的经典算法，由于其O(m+n)的时间复杂度，至今仍被广泛应用。大道至简，KMP算法非常简洁，然而，其内部却蕴含着玄妙的理论，以至许多人知其然而不知其所以然。本文旨在解开KMP算法的内部玄妙所在，希望能够有助于学习与理解。

1、KMP算法
    一种改进的字符串匹配算法，由D.E.Knuth与V.R.Pratt和J.H.Morris同时发现，因此称之为KMP算法。此算法可以在O(n+m)的时间数量级上完成串的模式匹配操作，其基本思想是：每当匹配过程中出现字符串比较不等时，不需回溯指针，而是利用已经得到的“部分匹配”结果将模式向右“滑动”尽可能远的一段距离，继续进行比较。

 

2、基于有限自动机理解算法
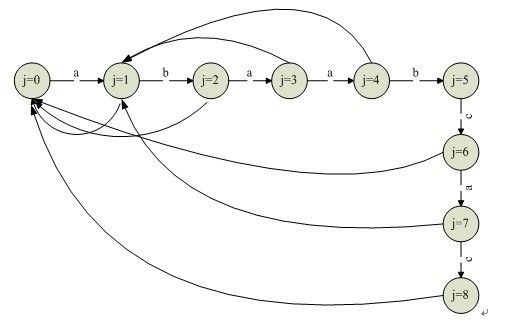
    KMP 算法看似简单，其实要完全理解还是有困难的。KMP算法其实可以看成是一个有限自动机，分为 2 部分：第一部分自动机的构造 ( 对应一般的说法就是失效函数，转移函数， overlap 函数 ) ，第二部分在自动机上搜索过程。举个例子： 目标串 T = acabaabaabcacaabc; 模式串 P=abaabcac ；根据模式串构造自动机，向前的箭头表示搜索前进的方向。向后的箭头表示不匹配的回溯，即失效函数，或者状态变迁函数。例如：
 f(j=1) = 0;
 f(j=2) = 0;
 f(j=3) = 1;
 f(j=4) = 1;
 f(j=5) = 2;
 f(j=6) = 0;
 f(j=7) = 1;

 

    KMP本质上是构造了DFA并进行了模拟，因此很显然一旦从模版T构造了自动机D，用D去匹配主串S的过程就是线性的。KMP最引人入胜的地方就在于构造D的自匹配过程，它充分利用了D是一个DAG的性质，使得构造过程也是线性的。KMP算法不需要计算变迁函数，只用到辅助数组Next，即模式串自身的特征向量。特征向量可以用模式与其自身进行比较，预先计算出来，它可用于加快字符串匹配算法与有限自动机匹配器的执行速度。

 

 

  
3、Next特征数组构造
    模式串P开头的任意个字符，把它称为前缀子串，如p0p1p2…pm-1。在P的第i位置的左边，取出k个字符，称为i位置的左子串，即pi-k+1... pi-2 pi-1 pi。求出最长的（最大的k）使得前缀子串与左子串相匹配称为，在第i位的最长前缀串。第i位的最长前缀串的长度k就是模板串P在位置i上的特征数n[i]特征数组成的向量称为该模式串的特征向量。
   可以证明对于任意的模式串p=p0p1…pm-1,确实存在一个由模式串本身唯一确定的与目标串无关的数组next，计算方法为：
   (1)  求p0…pi-1中最大相同的前缀和后缀的长度k;
   (2)  next[i] = k;

 

   作为特殊情况，当i=0时，令next[i] = -1;显然，对于任意i(0≤i<m)，有next[i] < i;假定已经计算得到next[i], 那么next[i+1] = ? 特征数ni ( -1≤ ni ≤ i )是递归定义的，定义如下：
   (1) n[0] ＝ -1，对于i > 0的n[i] ，假定已知前一位置的特征数 n[i-1]＝ k ；
   (2) 如果pi ＝ pk ，则n[i] ＝ k＋1 ；
   (3) 当pi ≠ pk 且k≠0时，则令k ＝ n [k -1] ; 让(3)循环直到条件不满足；
   (4) 当qi ≠ qk 且k ＝ 0时，则ni ＝ 0;

 

   根据以上分析，可以得到Next特征数组的计算方法，算法代码如下：

view plain copy to clipboard print ?

1. void get_next(SString T, int &next[])   
2. {   
3.     //求模式串T的next函数值并存入数组next    
4.     i = 1; next[1] = 0; j = 0;   
5.     while (i < T[0])    
6.     {   
7.         if(j ==0 || T[i] == T[j])    
8.         {   
9.             ++i; ++j; next[i] = j;   
10.         }    
11.         else     
12.         {   
13.             j = next[j];   
14.         }      
15.     }   
16. }  

void get_next(SString T, int &next[]){//求模式串T的next函数值并存入数组nexti = 1; next[1] = 0; j = 0;while (i < T[0]){if(j ==0 || T[i] == T[j]){++i; ++j; next[i] = j;} else {j = next[j];}}}

 

   文献[5]中解释了以上计算方法存在一定缺陷，存在多比较的情况，可对其进行修正，得到如下算法：

 

 

view plain copy to clipboard print ?

1. void get_next(SString T, int &next[])   
2. {   
3.     //求模式串T的next函数值并存入数组next    
4.     i = 1; next[1] = 0; j = 0;   
5.     while (i < T[0])    
6.     {   
7.         if(j ==0 || T[i] == T[j])    
8.         {   
9.             ++i; ++j;   
10.             if (T[i] != T[j])    
11.                 next[i] = j;   
12.             else   
13.                 next[i] = next[j];   
14.         }    
15.         else     
16.         {   
17.             j = next[j];   
18.         }      
19.     }   
20. }  

void get_next(SString T, int &next[]){//求模式串T的next函数值并存入数组nexti = 1; next[1] = 0; j = 0;while (i < T[0]){if(j ==0 || T[i] == T[j]){++i; ++j;if (T[i] != T[j])next[i] = j;elsenext[i] = next[j];} else {j = next[j];}}} 

 

   4、算法实现
   KMP算法的难点就是有限自动机的构造和特征向量的计算。解决了这两个问题后，具体匹配算法就很简单了。

 

   int   Index_KMP(SString   S,SString   T,int   pos){ 
              //利用模式串T的next函数求T在主串S中第pos个字符之后的位置的KMP算法。 
              //其中，T非空，1≤pos≤StrLength(S)。 
              i=pos;   j=1; 
              while(i <= S[0] && j<= T[0]){ 
                      if(j == 0 || S[i] == T[j]) { ++i; ++j; }//继续比较后继字符 
                      else   j = next[j];//模式串象右移动 
              } 
              if(j>T[0])   return   i-T[0];//匹配成功 
              else   return   0; 
   }//Index_KMP  

 

    算法相关理论分析与证明，以及算法复杂性分析，若感兴趣请参考文献[3]、[4]、[5]，这里不再赘述。

  KMP字符串模式匹配详解

KMP 字符串模式匹配通俗点说就是一种在一个字符串中定位另一个串的高效算法。简单匹配算法的时间复杂度为 O(m*n);KMP 匹配算法。可以证明它的时间复杂度为 O(m+n). 。

一 . 简单匹配算法

先来看一个简单匹配算法的函数：

int Index_BF ( char S [ ], char T [ ], int pos )

{

/* 若串 S 中从第 pos(S 的下标 0 ≤ pos<StrLength(S)) 个字符

起存在和串 T 相同的子串，则称匹配成功，返回第一个

这样的子串在串 S 中的下标，否则返回 -1    */

int i = pos, j = 0;

while ( S[i+j] != '\0'&& T[j] != '\0')

if ( S[i+j] == T[j] )

j ++; // 继续比较后一字符

else

{

i ++; j = 0; // 重新开始新的一轮匹配

}

if ( T[j] == '\0')

return i; // 匹配成功    返回下标

else

return -1; // 串 S 中 ( 第 pos 个字符起 ) 不存在和串 T 相同的子串

} // Index_BF
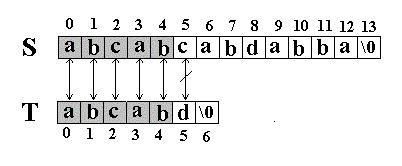
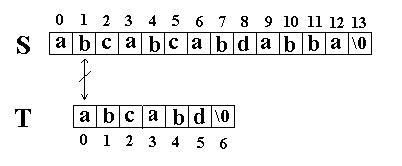
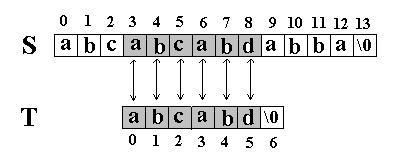
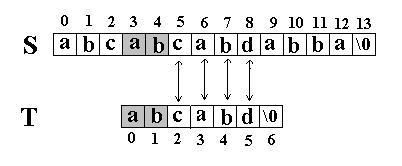
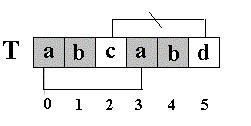
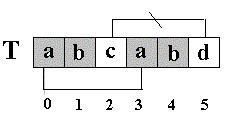
    此算法的思想是直截了当的：将主串 S 中某个位置 i 起始的子串和模式串 T 相比较。即从 j=0 起比较 S[i+j] 与 T[j] ，若相等，则在主串 S 中存在以 i 为起始位置匹配成功的可能性，继续往后比较 ( j 逐步增 1 ) ，直至与 T 串中最后一个字符相等为止，否则改从 S 串的下一个字符起重新开始进行下一轮的 " 匹配 " ，即将串 T 向后滑动一位，即 i 增 1 ，而 j 退回至 0 ，重新开始新一轮的匹配。

例如：在串 S= ”abcabcabdabba” 中查找 T=” abcabd” （我们可以假设从下标 0 开始） : 先是比较 S[0] 和 T[0] 是否相等，然后比较 S[1] 和 T[1] 是否相等 … 我们发现一直比较到 S[5] 和 T[5] 才不等。如图：

 

当这样一个失配发生时， T 下标必须回溯到开始， S 下标回溯的长度与 T 相同，然后 S 下标增 1, 然后再次比较。如图：

这次立刻发生了失配， T 下标又回溯到开始， S 下标增 1, 然后再次比较。如图：

这次立刻发生了失配， T 下标又回溯到开始， S 下标增 1, 然后再次比较。如图：

又一次发生了失配，所以 T 下标又回溯到开始， S 下标增 1, 然后再次比较。这次 T 中的所有字符都和 S 中相应的字符匹配了。函数返回 T 在 S 中的起始下标 3 。如图：

二 . KMP 匹配算法

还是相同的例子，在 S= ”abcabcabdabba” 中查找 T =”abcabd” ，如果使用 KMP 匹配算法，当第一次搜索到 S[5] 和 T[5] 不等后， S 下标不是回溯到 1 ， T 下标也不是回溯到开始，而是根据 T 中 T[5]==’d’ 的模式函数值（ next[5]=2 ，为什么？后面讲），直接比较 S[5] 和 T[2] 是否相等，因为相等， S 和 T 的下标同时增加 ; 因为又相等， S 和 T 的下标又同时增加。。。最终在 S 中找到了 T 。如图：

KMP 匹配算法和简单匹配算法效率比较，一个极端的例子是：

在 S= “ AAAAAA…AAB “ (100 个 A) 中查找 T=”AAAAAAAAAB”, 简单匹配算法每次都是比较到 T 的结尾，发现字符不同，然后 T 的下标回溯到开始， S 的下标也要回溯相同长度后增 1 ，继续比较。如果使用 KMP 匹配算法，就不必回溯 .

对于一般文稿中串的匹配，简单匹配算法的时间复杂度可降为 O (m+n) ，因此在多数的实际应用场合下被应用。

KMP 算法的核心思想是利用已经得到的部分匹配信息来进行后面的匹配过程。看前面的例子。为什么 T[5]==’d’ 的模式函数值等于 2 （ next[5]=2 ），其实这个 2 表示 T[5]==’d’ 的前面有 2 个字符和开始的两个字符相同，且 T[5]==’d’ 不等于开始的两个字符之后的第三个字符（ T[2]=’c’ ） . 如图：

也就是说，如果开始的两个字符之后的第三个字符也为 ’d’, 那么，尽管 T[5]==’d’ 的前面有 2 个字符和开始的两个字符相同， T[5]==’d’ 的模式函数值也不为 2 ，而是为 0 。

   前面我说：在 S= ”abcabcabdabba” 中查找 T =”abcabd” ，如果使用 KMP 匹配算法，当第一次搜索到 S[5] 和 T[5] 不等后， S 下标不是回溯到 1 ， T 下标也不是回溯到开始，而是根据 T 中 T[5]==’d’ 的模式函数值，直接比较 S[5] 和 T[2] 是否相等。。。为什么可以这样？

刚才我又说：“（ next[5]=2 ），其实这个 2 表示 T[5]==’d’ 的前面有 2 个字符和开始的两个字符相同”。请看图   ：因为， S[4] ==T[4] ， S[3] ==T[3] ，根据 next[5]=2 ，有 T[3]==T[0] ， T[4] ==T[1] ，所以 S[3]==T[0] ， S[4] ==T[1] （两对相当于间接比较过了），因此，接下来比较 S[5] 和 T[2] 是否相等。。。

有人可能会问： S[3] 和 T[0] ， S[4] 和 T[1] 是根据 next[5]=2 间接比较相等，那 S[1] 和 T[0] ， S[2] 和 T[0] 之间又是怎么跳过，可以不比较呢？因为 S[0]=T[0] ， S[1]=T[1] ， S[2]=T[2] ，而 T[0] != T[1], T[1] != T[2],==> S[0] != S[1],S[1] != S[2], 所以 S[1] != T[0],S[2] != T[0].  还是从理论上间接比较了。

有人疑问又来了，你分析的是不是特殊轻况啊。

假设 S 不变，在 S 中搜索 T= “ abaabd ”呢？答：这种情况，当比较到 S[2] 和 T[2] 时，发现不等，就去看 next[2] 的值， next[2]=-1 ，意思是 S[2] 已经和 T[0] 间接比较过了，不相等，接下来去比较 S[3] 和 T[0] 吧。

假设 S 不变，在 S 中搜索 T= “ abbabd ”呢？答：这种情况当比较到 S[2] 和 T[2] 时，发现不等，就去看 next[2] 的值， next[2]=0 ，意思是 S[2] 已经和 T[2] 比较过了，不相等，接下来去比较 S[2] 和 T[0] 吧。

假设 S=” abaabcabdabba ” 在 S 中搜索 T= “ abaabd ”呢？答：这种情况当比较到 S[5] 和 T[5] 时，发现不等，就去看 next[5] 的值， next[5]=2 ，意思是前面的比较过了，其中， S[5] 的前面有两个字符和 T 的开始两个相等，接下来去比较 S[5] 和 T[2] 吧。

总之，有了串的 next 值，一切搞定。那么，怎么求串的模式函数值 next[n] 呢？（本文中 next 值、模式函数值、模式值是一个意思。）

5、参考文献
[1] http://wansishuang.javaeye.com/blog/402018
[2] http://richardxx.yo2.cn/articles/kmp和extend-kmp算法.html
[3] KMP算法讲义PPT(Hu Junfeng, Peking University)
[4] 算法导论(第32章 字符串匹配)
[5] 数据结构(第4章 串)

http://blog.csdn.net/liuben/archive/2009/08/04/4409505.aspx