【leetcode】Single Number && Single Number II(ORZ 位运算)
题目描述:
Single Number
Given an array of integers, every element appears twice except for one. Find that single one.
Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?
Single Number II
Given an array of integers, every element appears three times except for one. Find that single one.
Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?
题目的意思都很直白,就是一个数组中只有一个元素只出现一次,其他都出现了两(三)次,求那个元素是什么。
我们首先从第一个问题开始思考,要在比较快的时间内找到只有一个的数,我们可以想到几种方式:
首先最容易想到的就是先排个序,那样就直接一遍遍李青松得出结果,但是排序的复杂度最快也就nlogn(基数排序类除外),所以这种方式在实践复杂度上来说不行(不过你只是想过题的话这种方法还是可以的)。
然后我们会想到时间换空间,也就是用一个标记数组进行操作,每次读入一个数字就把表技术组的相应位置为标记值,并且考虑到数字的范围问题我们还可以通过合适的hash策略进行求解,这种方法除了在实现上需要考虑到合适的hash函数之外应该都是不错的。知识由于表技术组的存在,需要o(n)的存储空间,还不是一个足够好的方法。
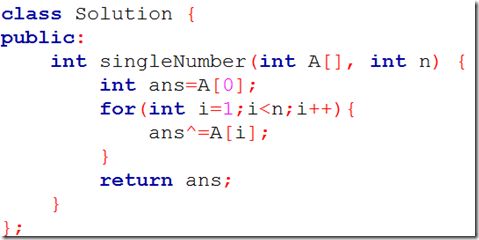
最后,我们考虑到除了我们要的那个值其他的值都会出现两次,就想到如果那两个一样的直接抵消了就好了,那么剩下的就是我们所需要的那个数了,那么有什么能干到这一点?对,就是位运算--异或,我们知道异或的运算法则是相同则为零,不同则唯一。并且位运算的结果和顺序是没有关系的,那么我们把两个相同的值疑惑起来结果必然为零,于是最后剩下的就是我们要的那个数了,代码如下:
那么我们现在来看第二个题,这个题与上面的不同就在那个三上面,分析一下我们发现,对于我们上面提到的第一种和第二种不优秀的解法没什么影响(往往不是最优秀的解法通用性都比较好)。但是第三种解法已经不能用了
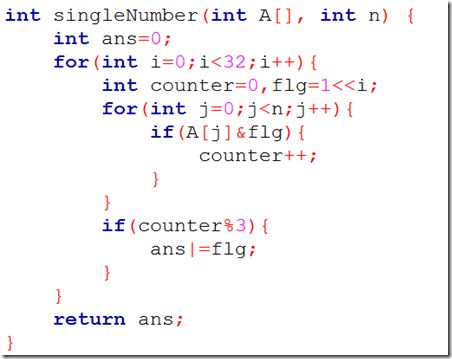
分析一下发现我们已经不可能直接向上面那样用任意一种位运算求出这个解了,于是乎哀叹要是另外有那么个运算xxx是“有三个相同的则为0,否则为一”那就好了,我们就可以按照上一题一样的思路进行求解了。不过这个确实不存在,但是我们可以自己实现啊,当然直接实现一个这么高档的位运算符有点难,那我们就一位一位来吧。也就是说一位一位判断是不是出现了三次的倍数,是的话我们就置0,否则置1.代码如下:
当然由于位运算十分精妙肯定是还有很多不同解法了,但是我觉得上面的两种还是比较易于思考和理解的。希望能有所帮助