网络爬虫-jd滑块验证码
仅供研究学习使用。
目标站点 --> 京东网页登录
当我们输入账号密码后,点击登录,首先映入眼帘的是一个滑块,那我们先分析一下滑块吧。
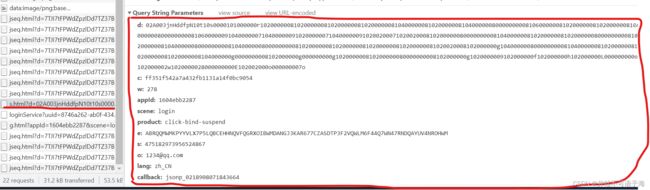
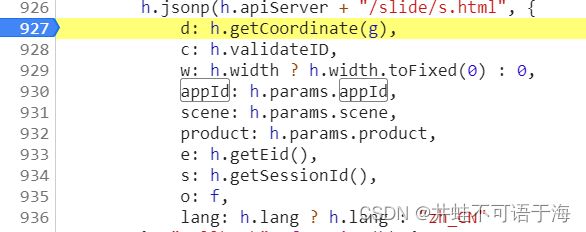
上图是滑块的有关信息,左边的横线是请求的url,右边是参数,很显然,里面有好多参数。但经过分析,d就是滑块轨迹的加密,c跟下图获取滑块图片一起返回的,下图中challenge就是参数c,参数e可以从网页源码中获取到,而参数appId是定值,参数o就是我们的账号
下面我们就分析一下参数d,看它怎么加密。
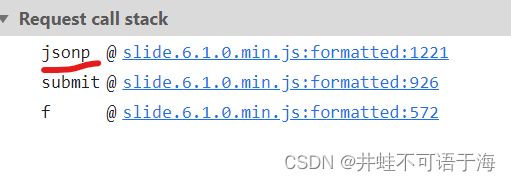
这里我是通过下图调用栈,找到的,点击下图画横线的,然后格式化一下,再搜索appId就可以找到。
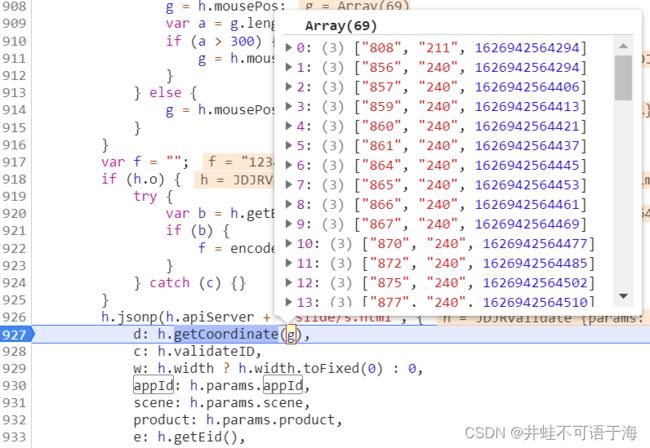
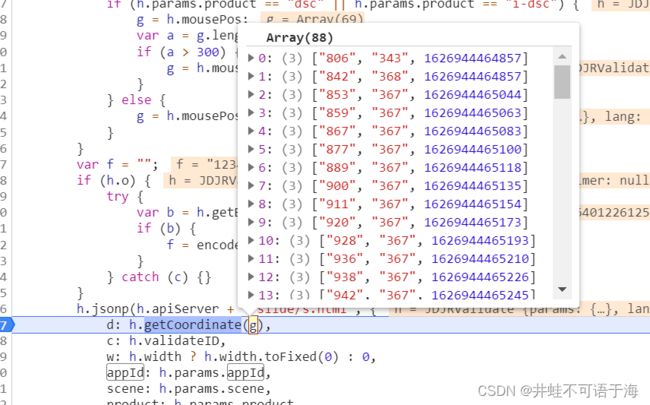
可以清除看到,g为一个数组,其实就是我一定滑块的轨迹,这里我们可以借鉴一个文章里面的滑块轨迹思路
import random
import matplotlib.pyplot as plt
import numpy as np
class GTrace(object):
def __init__(self):
self.__pos_x = []
self.__pos_y = []
self.__pos_z = []
def __set_pt_time(self):
"""
设置各节点的时间
分析不同时间间隔中X坐标数量的占比
统计结果: 1. 80%~90%的X坐标在15~20毫秒之间
2. 10%~15%在20~200及以上,其中 [-a, 0, x, ...] 这里x只有一个,取值在110~200之间
坐标集最后3~5个坐标取值再50~400之间,最后一个坐标数值最大
滑动总时间的取值规则: 图片宽度260,去掉滑块的宽度剩下200;
如果距离小于100,则耗时1300~1900之间
如果距离大于100,则耗时1700~2100之间
"""
__end_pt_time = []
__move_pt_time = []
self.__pos_z = []
total_move_time = self.__need_time * random.uniform(0.8, 0.9)
start_point_time = random.uniform(110, 200)
__start_pt_time = [0, 0, int(start_point_time)]
sum_move_time = 0
_tmp_total_move_time = total_move_time
while True:
delta_time = random.uniform(15, 20)
if _tmp_total_move_time < delta_time:
break
sum_move_time += delta_time
_tmp_total_move_time -= delta_time
__move_pt_time.append(int(start_point_time+sum_move_time))
last_pt_time = __move_pt_time[-1]
__move_pt_time.append(last_pt_time+_tmp_total_move_time)
sum_end_time = start_point_time + total_move_time
other_point_time = self.__need_time - sum_end_time
end_first_ptime = other_point_time / 2
while True:
delta_time = random.uniform(110, 200)
if end_first_ptime - delta_time <= 0:
break
end_first_ptime -= delta_time
sum_end_time += delta_time
__end_pt_time.append(int(sum_end_time))
__end_pt_time.append(int(sum_end_time + (other_point_time/2 + end_first_ptime)))
self.__pos_z.extend(__start_pt_time)
self.__pos_z.extend(__move_pt_time)
self.__pos_z.extend(__end_pt_time)
def __set_distance(self, _dist):
"""
设置要生成的轨迹长度
"""
self.__distance = _dist
if _dist < 100:
self.__need_time = int(random.uniform(500, 1500))
else:
self.__need_time = int(random.uniform(1000, 2000))
def __get_pos_z(self):
return self.__pos_z
def __get_pos_y(self):
_pos_y = [random.uniform(-40, -18), 0]
point_count = len(self.__pos_z)
x = np.linspace(-10, 15, point_count - len(_pos_y))
arct_y = np.arctan(x)
for _, val in enumerate(arct_y):
_pos_y.append(val)
return _pos_y
def __get_pos_x(self, _distance):
"""
绘制标准的数学函数图像: 以 tanh 开始 以 arctan 结尾
根据此模型用等比时间差生成X坐标
"""
# first_val = random.uniform(-40, -18)
# _distance += first_val
_pos_x = [random.uniform(-40, -18), 0]
self.__set_distance(_distance)
self.__set_pt_time()
point_count = len(self.__pos_z)
x = np.linspace(-1, 19, point_count-len(_pos_x))
ss = np.arctan(x)
th = np.tanh(x)
for idx in range(0, len(th)):
if th[idx] < ss[idx]:
th[idx] = ss[idx]
th += 1
th *= (_distance / 2.5)
i = 0
start_idx = int(point_count/10)
end_idx = int(point_count/50)
delta_pt = abs(np.random.normal(scale=1.1, size=point_count-start_idx-end_idx))
for idx in range(start_idx, point_count):
if idx*1.3 > len(delta_pt):
break
th[idx] += delta_pt[i]
i+=1
_pos_x.extend(th)
return _pos_x[-1], _pos_x
def get_mouse_pos_path(self, distance):
"""
获取滑动滑块鼠标的滑动轨迹坐标集合
"""
result = []
_distance, x = self.__get_pos_x(distance)
y = self.__get_pos_y()
z = self.__get_pos_z()
for idx in range(len(x)):
result.append([int(x[idx]), int(y[idx]), int(z[idx])])
import matplotlib.pyplot as plt
plt.plot(z,x)
plt.show()
return int(_distance), result
我们把数组copy下来,本地画一下图,然后看看是怎样的轨迹。
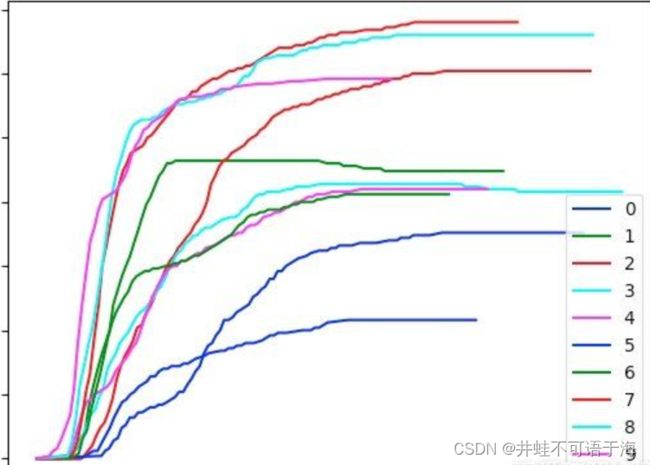
基本上都是这样的一个轨迹。我们用那个文章的代码跑一下,然后生成跟g一样的数组,本地生成的数组替换滑块的,看看能不能过,经过我的尝试,是可以的,至于那个移动长度,其实数组的第一个(从第0个开始)的第0个参数,被最后一个数组的第0个减去,然后就是移动距离。
[
[
"808",
"211",
1626942564294
],
[
"856",
"240",
1626942564294
],
[
"857",
"240",
1626942564406
],
[
"859",
"240",
1626942564413
],
[
"860",
"240",
1626942564421
],
[
"861",
"240",
1626942564437
],
[
"864",
"240",
1626942564445
],
[
"865",
"240",
1626942564453
],
[
"866",
"240",
1626942564461
],
[
"867",
"240",
1626942564469
]
]
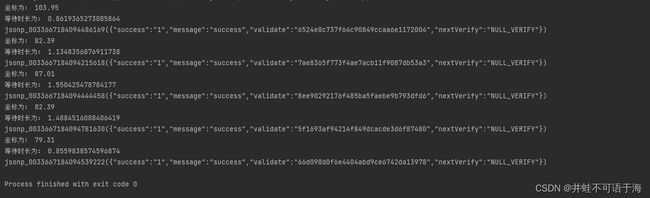
通过上图可以看出,g发生了改变,没错,就是我们本地生成的数组。我们接着让它运行,看一下结果。
function string10to64(d) {
var c = "0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ-~".split("")
, b = c.length
, e = +d
, a = [];
do {
mod = e % b;
e = (e - mod) / b;
a.unshift(c[mod])
} while (e);
return a.join("")
}
function prefixInteger(a, b) {
return (Array(b).join(0) + a).slice(-b)
}
function pretreatment(d, c, b) {
var e = string10to64(Math.abs(d));
var a = "";
if (!b) {
a += (d > 0 ? "1" : "0")
}
a += prefixInteger(e, c);
return a
}
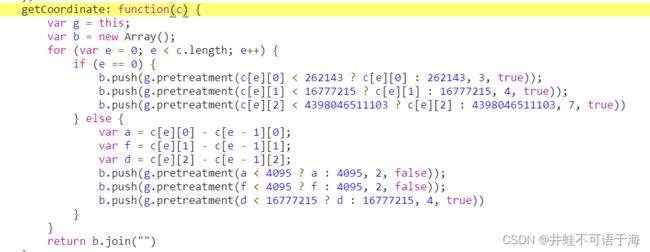
function getCoordinate(c) {
var b = new Array();
for (var e = 0; e < c.length; e++) {
if (e == 0) {
b.push(pretreatment(c[e][0] < 262143 ? c[e][0] : 262143, 3, true));
b.push(pretreatment(c[e][1] < 16777215 ? c[e][1] : 16777215, 4, true));
b.push(pretreatment(c[e][2] < 4398046511103 ? c[e][2] : 4398046511103, 7, true))
} else {
var a = c[e][0] - c[e - 1][0];
var f = c[e][1] - c[e - 1][1];
var d = c[e][2] - c[e - 1][2];
b.push(pretreatment(a < 4095 ? a : 4095, 2, false));
b.push(pretreatment(f < 4095 ? f : 4095, 2, false));
b.push(pretreatment(d < 16777215 ? d : 16777215, 4, true))
}
}
return b.join("")
}
function slide(array) {
g = array
return getCoordinate(g)
}