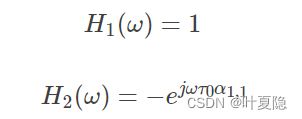差分波束的基本原理
概述
传统波束成形方法有延时累加(delay-sum),滤波相加(filter-sum)以及自适应波束形成(LCMV、MVDR、GSC ……)等等,这些方法都是将阵列数据做同步后相加输出,与相加相对应的是相减,这类方法就是下面要介绍的差分阵列(Differential microphone arrays),简称DMAs。
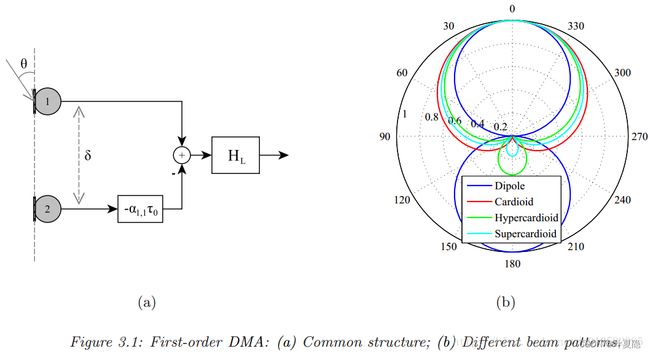
DMA(differential microphone arrays)是麦克风阵列处理中一种很重要的信号处理方法,特别是在多通道语音增强中的应用。差分麦克风阵列应用场景其目标信号一般是来自于端射方向,比较典型的如当今比较热门的蓝牙耳机,耳机的端射方向和说话人嘴的位置基本在一条线上。本博文首先基于一阶差分(First order DMA)对双麦克风语音增强进行讲解差分麦克风的具体应用。
差分麦克风阵列不同于加性麦克风阵列,如filter_sum,mvdr,gsc之类的算法,差分麦克风阵列是通过设定null方向来决定其主瓣的形状的,而filter_sum,mvdr等之类的算法是通过设定主瓣本身来决定其主瓣形状的。
差分阵列表现的是空间声压的差异性,声压的一阶差分可以由两个相近放置的全向麦克风输出相减得到,同理,N个麦克风可以最多可以获得声压的N-1阶差分。
要设计一个差分阵列,一个很重要的条件就是麦克风间距要小到麦克风间的有限差值输出能够估计实际声压场的差别,与声音信号波长相比,麦克风间距要远小于波长

DMA特点
差分麦克风阵列是通过两个或者更多个全指向麦克风来实现之间的声压差来实现其指向性的。相比加性麦克风阵列,差分麦克风阵列具有如下优点:
(1) 对于频率具有不变性的beampattern,因此非常适合处理宽带语音信号
(2) 其指向性不仅对高频有效,对低频同样有效
(3) 对于给定具体数量的麦克风,差分麦克风阵列更容易获得最大的指向性增益
(4) 紧凑的阵列放置
同样差分麦克风具有自身的缺陷:
(1) 差分麦克风的上述优点的前提是麦克风之间的间隔要足够小,否则会导致频率的空间混叠。
(2) 差分麦克风阵列具有高通特性,因此通过其处理后需要进行补偿
(3) 频率响应和DMA的阶数对麦克风阵列相对声源的位置和角度较为敏感
(4) 阵列响应由阵列相对声源方向而定
(5) 低频白噪声增益
在filter-sum beamformer中,麦克风数据经最优滤波输出以使主瓣方向对准目标方向,而在差分阵列中,一般主瓣方向固定,差分阵列的滤波器设计是为了在指定的方向上放置零点。
原理
beampattern定义
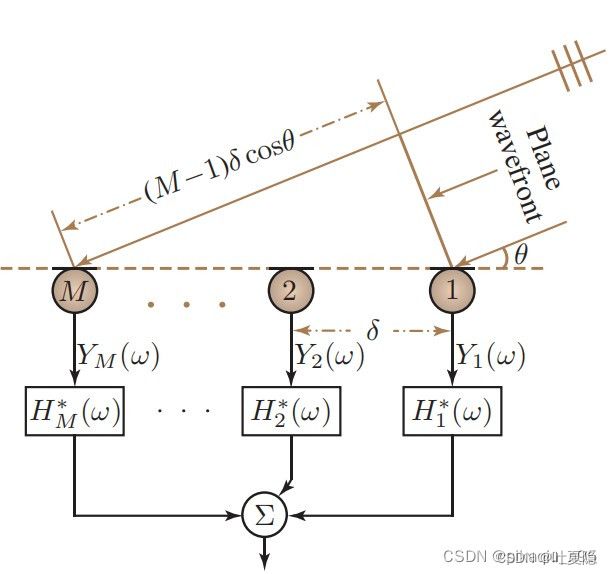
有M个全指向麦克风,麦克风之间的间距为d,声速c=340m/s,那么可以求得该阵列的导向矢量为:
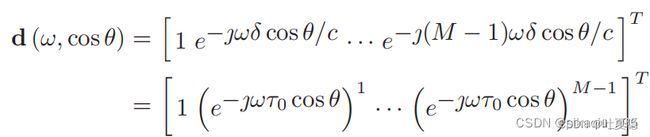
其中w=2∗pi∗f,tao = δ / c , λ = c / f,DMA假设麦克风之间的间隔δ远远小于λ,即:
wδ / c = w ∗ tao0 << 2 ∗ pi
该条件对于低频还比较容易满足,因为λ = c / f,高频相对容易出现混叠。
对于上图中的每个麦克风输出端的权重H,写为一个向量的形式如下:
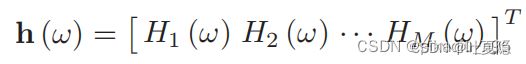
beampattern描述的是阵列对不同方向的敏感程度,具体定义如下:
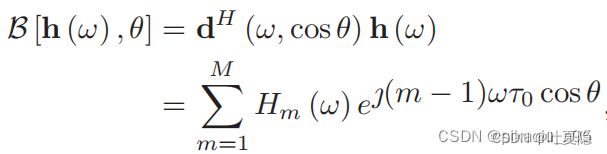
θ为入射角方向,即描述的是麦克风阵列对于不同入射角方向的敏感程度,或者说频率响应。
对于一阶DMA其beampattern为:
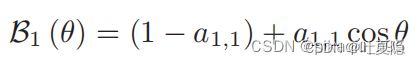
根据a1,1取不同的值可以得到不同的beampattern,比较典型的如下:

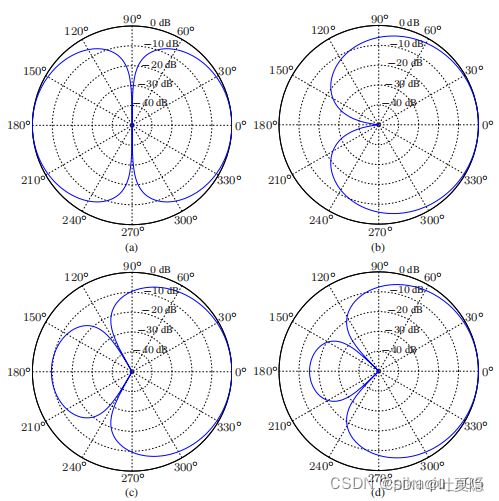
以双麦克风阵列为例,一阶DMA其端射方向在0度方向上,抑制(null)方向在(0,180]范围内,因此其约束条件可以写为:
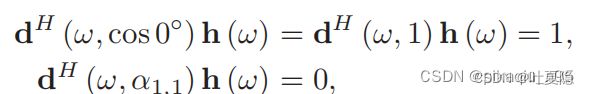
其中a1,1=cosθ为抑制(null)方向,-1 <= a1,1 <= 1,上式可以进一步整理为:
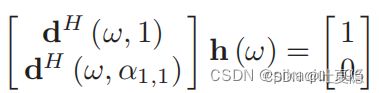
这里以First-Order Cardioid为例进行讲解,其他类型的一阶DMA只是抑制(null)的方向不同,即a1,1取值的区别而已,推导过程是一致的。
在first-order Cardioid的端射方向在0°,抑制(null)方向在180°,即a1,1=-1. 因此,线性方程组为:
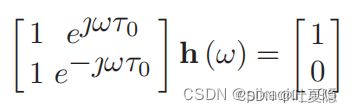
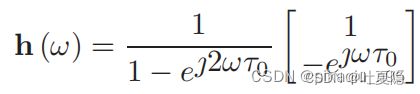
两个麦克风的滤波系数分别为以下两式
利用近似 e^x = 1 + x 求解可得:
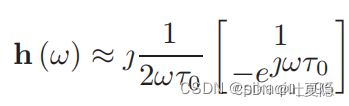
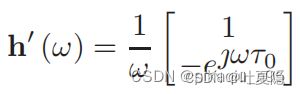
其beampattern为:
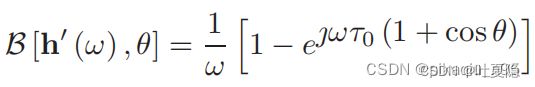
求H:
frameLength = 256;
inc = frameLength/2;
c = 340;
tao0 = d/c;
N = frameLength;
omega = zeros(N/2+1,1);
HL = zeros(1,N/2+1);
H = zeros(2,N/2+1);
frameNum = size(X,1);
half_bin = size(X,3);
for k = 4:N/2+1
omega(k) = 2*pi*(k-1)*fs/N;
HL(k) = 1/(1-exp(1j*omega(k)*tao0*(alpha_1_1-cos(theta_target)))) * 0.5;
%HL(k) = 1j/(omega(k)*tao0*(alpha_1_1-cos(theta_target))); % approximating e^x with 1+x
H(:,k) = HL(k)*[1;
-exp(1j*omega(k)*tao0*alpha_1_1)];
end
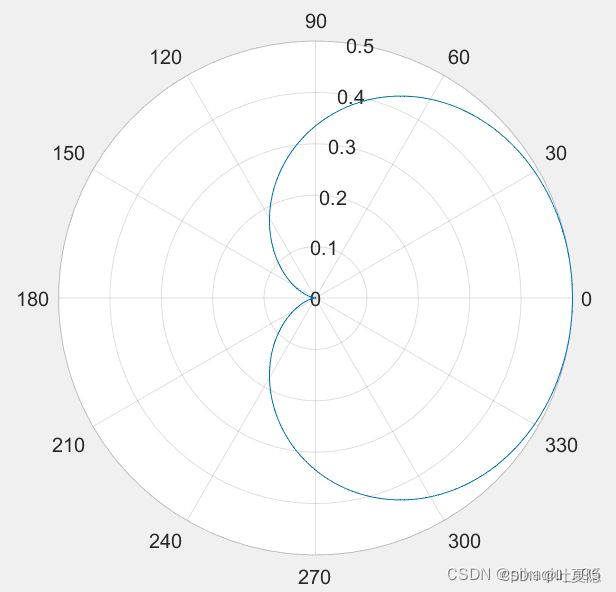
beamout = beampolar(H,d,tao0);
figure;
polarplot(linspace(0,2*pi,360),abs(beamout(:,64)));
beampattern:
function [beampattern] = beampolar(weights,spacing,tao0)
f = 1:1:20000;
theta = linspace(0,2*pi,360); % scaning angle
d = spacing;
c = 340;
% tao0 = d/c;
tao = tao0*cos(theta);
omega = 2*pi*f;
half_bin = size(weights,2);
fs = 16000;
N_FFT = (half_bin-1)*2;
Nele = size(weights,1);
H = zeros(Nele,length(omega));
beampattern = zeros(length(theta),length(half_bin)); % beamformer output
for ang = 1:length(theta)
for freIndex = 1:half_bin
omega_k = 2*pi*(freIndex-1)*fs/N_FFT; % normalized digital angular frequency
% omega_k = omega(freIndex); % analog angular frequency
a = [1,exp(-1j*omega_k*tao(ang))]; % signal model,steering vector
beampattern(ang,freIndex) = a*(weights(:,freIndex)); % y = w'*a,此处为beampattern原始定义方式求解;
end
end
end
绘制beampattern图如下:
滤波结果:
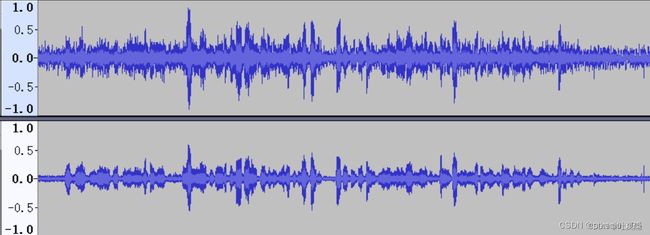
上图中,上面部分是输入两路信号的一路,另外一路是first-order Cardioid滤波处理的结果。
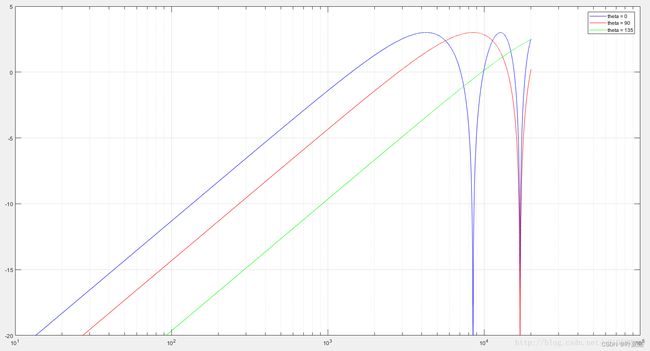
编写程序绘制一阶DMA频率响应:
close all;
theta = [0,90,135]'*pi/180;%0:2*pi/360:2*pi; %注视方向
alpha = 180*pi/180; %零点方向
f = 1:1:20000;
d = 0.02;
c = 340;
tao0 = d/c;
omega = 2*pi*f;
B = zeros(3,length(f));
for i = 1:length(f)
%B(:,i) = 1j/(omega(i)*tao0*(alpha-1))*(1-exp(-1*1j*omega(i)*tao0*(cos(theta)-cos(alpha))));
B(:,i) = (1-exp(-1*1j*omega(i)*tao0*(cos(theta)-cos(alpha))));
end
figure,plot(pow2db(abs(B(1,:))),'b'),ylim([-20,5]),
set(gca,'XScale','log'),grid on
hold on
plot(pow2db(abs(B(2,:))),'r'),ylim([-20,5]),
hold on,
plot(pow2db(abs(B(3,:))),'g'),ylim([-20,5]),
legend('theta = 0','theta = 90','theta = 135');
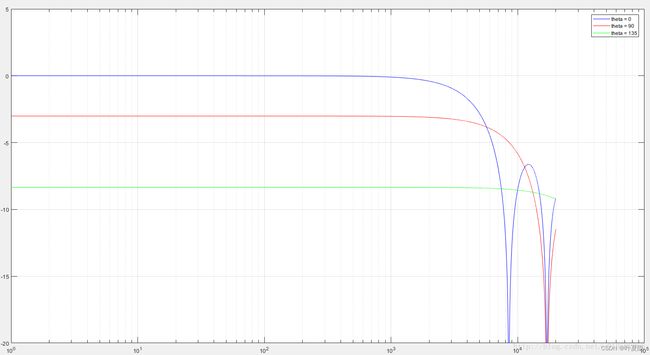
添加补偿滤波器后:
code example:
https://github.com/yexiayin/differential-array
参考:
[1]: 《Differential Microphone Arrays》
[2]: 《Study and Design of Differential Microphone Arrays》