dijkstra模板及例题(最短路算法)
大家好,我是永遇乐金枪鱼。图论和树论是算法中占比大且非常重要的内容,而且树论是特殊的图论,而图论中最经典的就是求解最短路,而最短路算法是比较广泛且冗杂的算法,与其相关的有较多的算法,下面我给大家讲讲常用算法之一——dijkstra算法。
博客首页:永遇乐金枪鱼的博客
欢迎关注点赞收藏⭐️留言
❤️ :热爱Java与算法学习,期待一起交流!
作者水平很有限,如果发现错误,求告知,多谢!
有问题可私信交流!!!
高校算法学习社区:高校算法学习社区
一起加入刷题内卷大军,还可以加入专属内卷群
引入
dijkstra和bellman-ford只能解决单源最短路径,dijkstra可以只能解决非负权值的路径问题,bellman-ford可以解决负权值得路径问题,而floyd可以解决任意两点间的最短路径问题。
概况
什么是最短路径呢?
最短路径通俗的来说,就是在一个图中,从一个点到另外一个点的最小代价(最短路不仅仅求距离,还有金钱利润、花费时间、挫折度等)
什么是dijkstra算法?
注意:上面说到dijkstra算法只能做非负权问题,所以如果遇到负权问题或负权环,这个算法就不适用了。
首先,我们要知道dijkstra有两种实现方式:朴素版(O(n ^ 2)),堆优化(O(mlogn)) (n是顶点数,m是边数,相当于G(V,E)).
那么这个算法具体如何实现呢?
先标记起点,然后找到一个距离起点最近的点且该点未确定好最短距离,更新到该点的距离,然后再利用该点去更新其他点的最短距离。
《离散数学(第2版)》中说到:
模板
朴素版:O(n ^ 2)
/*
1.声明dis[],vis[],f[][],dis用于记录从起点到i的最短路,vis标记是否用过,f用于存储前驱到后驱的权值
2.初始化dis[]为无穷大(INF)以及dis[起点]=0,用变量t=-1来表示距离起点最近且未标记的点
如果dist[j]
#define MOD 10000000007
#define INF 0x3f3f3f3f
using namespace std;
typedef long long LL;
int n,m,s;//n是顶点数,m是边数,s是起点
LL dis[10005],vis[10005],f[10001][10001];//dis用于记录从起点到i的最短路,vis标记是否用过,f用于存储前驱到后驱的权值
//快读读入数值
inline int read() {
int date=0,w=1;//date存数,w存符号
char c;
c=getchar();
while(c<'0' || c>'9') {
if(c=='-') w=-1;
c=getchar();
}
while(c>='0' && c<='9') {
date=date*10+(c-'0');
c=getchar();
}
return date*w;
}
void dijkstra() {
//初始化
memset(dis,INF,sizeof(dis));
dis[s]=0;//起点到自己当然是0
for(int i=1; i<=n; i++) {
int t=-1;//用于找第一个未被标记的点
for(int j=1; j<=n; j++)
if(!vis[j] && (t==-1 || dis[j] 堆优化版:O(mlogn)
#include
#define MOD 10000000007
#define INF 0x3f3f3f3f
using namespace std;
typedef long long LL;
const int maxn=2000005;
int n,m,s;
//idx表示边的序数,e存终点,w存权值,h存表头,next存下一个点(h和next形成了链表)
//idx其实并没有实质性意义,只是用于确定一条边的前驱、后驱和权值(便于调用及确定与其顶点的关系)
int idx,e[maxn],w[maxn],h[maxn],ne[maxn];
int dis[maxn],vis[maxn];//距离,标记
struct Node {
int dis,x;//距离和当前点
//重载运算符(从小到大排序)
bool operator < (Node p) const {
return dis > p.dis;
}
Node(int dis,int x):dis(dis),x(x) {}
};
//快读
inline int read() {
int date=0,w=1;
char c;
c=getchar();
while(c<'0' || c>'9') {
if(c=='-') w=-1;
c=getchar();
}
while(c>='0' && c<='9') {
date=date*10+(c-'0');
c=getchar();
}
return date*w;
}
//邻接表(顶点为表头,后面跟着的都是该顶点为起点的边)
void add(int a,int b,int c) {
e[++idx]=b;
w[idx]=c;
ne[idx]=h[a];//同一个起点的边形成邻接表关系
h[a]=idx;
}
void dijkstra() {
memset(dis,INF,sizeof(dis));//初始化
priority_queue q;//按照结构体中的重载符进行排序(从小到大排序,先将dis小的出队)
dis[s]=0;//初始化起点
Node u(dis[s],s);
q.push(u);
while(!q.empty()) {
Node u=q.top();
q.pop();
if(vis[u.x]) continue;//已标记过的点,即这个点为起点的这条链已走完
vis[u.x]=1;//标记
//for(表头;链尾非NULL;链的下一个结点)
for(int i=h[u.x]; i; i=ne[i]) {
if(dis[e[i]] > dis[u.x] + w[i]) {
dis[e[i]] = dis[u.x] + w[i];
Node v(dis[e[i]],e[i]);//dis[终点],终点(距离起点最近)
q.push(v);
}
}
}
}
int main() {
n=read(),m=read(),s=read();
for(int i=1; i<=m; i++) {
int a=read(),b=read(),c=read();
add(a,b,c);//建立邻接表关系(以边为单位)
}
/*for(int i=0; i<=n; i++)
cout< 以上就是该算法的两个模板,一般都用堆优化模板,因为快!下面的例题的前三道只能用堆优化来做,因为数据有点大,用朴素版的O(n ^ 2)会TLE(超时)。最后一道能用朴素版实现。
例题
第一题(堆优化模板)
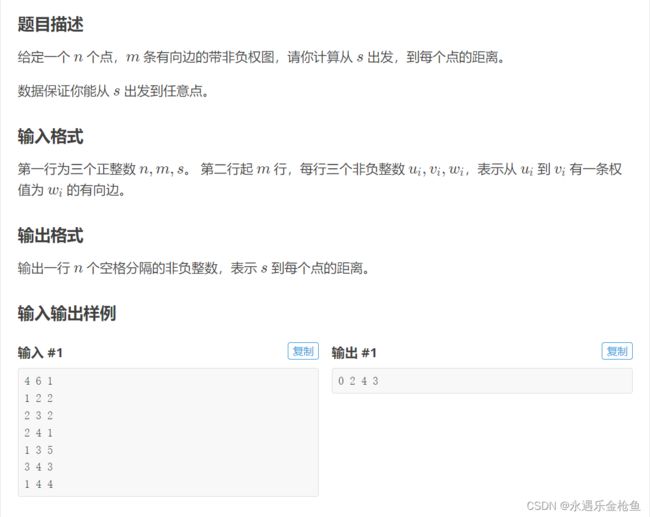
P4779 【模板】单源最短路径(标准版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
只要把上面的模板套过来即可。
#include
#define MOD 10000000007
#define INF 0x3f3f3f3f
using namespace std;
typedef long long LL;
const int maxn=2000005;
int n,m,s;
//idx表示边的序数,e存终点,w存权值,h存表头,next存下一个点(h和next形成了链表)
int after[maxn],idx=1,e[maxn],w[maxn],h[maxn],ne[maxn];
int dis[maxn],vis[maxn];//距离,标记
struct Node {
int dis,x;//距离和当前点
//重载运算符(将小于改为大于)
bool operator < (Node p) const {
return dis > p.dis;
}
Node(int dis,int x):dis(dis),x(x) {}
};
//快读
inline int read() {
int date=0,w=1;
char c;
c=getchar();
while(c<'0' || c>'9') {
if(c=='-') w=-1;
c=getchar();
}
while(c>='0' && c<='9') {
date=date*10+(c-'0');
c=getchar();
}
return date*w;
}
//邻接表
void add(int a,int b,int c) {
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];//同一个起点的边形成邻接表关系
h[a]=idx++;//先做idx 再++
}
void dijkstra() {
memset(dis,INF,sizeof(dis));//初始化
priority_queue q;//按照结构体中的重载符进行排序(从小到大排序,先将dis小的出队)
dis[s]=0;
Node u(dis[s],s);
q.push(u);
while(!q.empty()) {
Node u=q.top();
q.pop();
if(vis[u.x]) continue;//已标记过的点,即这个点为起点的这条链已走完
vis[u.x]=1;//标记
//for(表头;链尾非NULL;链的下一个结点)
for(int i=h[u.x]; i!=-1; i=ne[i]) {
if(dis[e[i]] > dis[u.x] + w[i]) {
dis[e[i]] = dis[u.x] + w[i];
Node v(dis[e[i]],e[i]);//dis[终点],终点(距离起点最近)
q.push(v);
//after[u.x]=e[i];
}
}
}
}
int main() {
memset(h,-1,sizeof(h));//初始化每个点的下一个结点都是NULL
n=read(),m=read(),s=read();
for(int i=1; i<=m; i++) {
int a=read(),b=read(),c=read();
add(a,b,c);
}
/*for(int i=0; i<=n; i++)
cout< 第二题(堆优化+无向边)
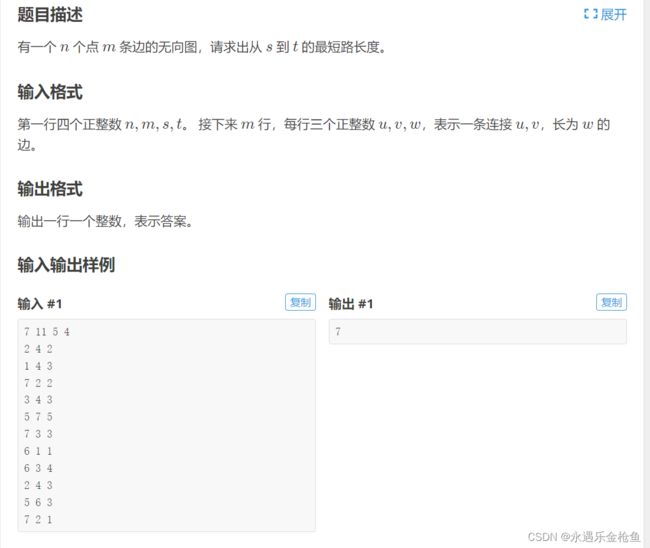
P1339 [USACO09OCT]Heat Wave G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这里求的是两个点的距离,可能会有人想到floyd,然后看看数据量,好的是dijkstra。题目说到是无向边,所以怎么用dijkstra来做呢?其实很简单,在构建邻接表的时候再补一条有向边就好啦,一条起点到终点的有向边,一条终点到起点的有向边,不就是变成无向边了吗?好!我们看看代码。
#include
#include
#include
#include
#include
#include
using namespace std;
int n,m,s,t,idx;
int dis[3000],vis[3000];
int e[15000],w[15000],h[15000],ne[15000];
//最短路从小到大排序
struct node {
int x,d;
bool operator < (node p) const {
return d > p.d;
}
node(int x,int d):x(x),d(d) {}
};
//快读
inline int read() {
int date=0,w=1;
char c=getchar();
while(c<'0' || c>'9') {
if(c=='-') w=-1;
c=getchar();
}
while(c>='0' && c<='9') {
date=date*10+(c-'0');
c=getchar();
}
return date*w;
}
//邻接表模板
void add(int a,int b,int c) {
e[++idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx;
}
void dijkstra() {
memset(dis,0x7f,sizeof(dis));//初始化dis数组
priority_queue q;
dis[s]=0;//初始化起点
node u(s,dis[s]);
q.push(u);
while(!q.empty()) {
node u=q.top();
q.pop();
if(vis[u.x]) continue;
vis[u.x]=1;
for(int i=h[u.x]; i; i=ne[i]) {
if(dis[e[i]] > dis[u.x] + w[i]) {
dis[e[i]] = dis[u.x] + w[i];
node v(e[i],dis[e[i]]);
q.push(v);
}
}
}
}
int main() {
n=read(),m=read(),s=read(),t=read();
for(int i=1; i<=m; i++) {
int a=read(),b=read(),c=read();
//构建无向边
add(a,b,c);//a到b权值为w
add(b,a,c);//b到a权值为w
}
dijkstra();
cout< 第三题(堆优化+无向边)
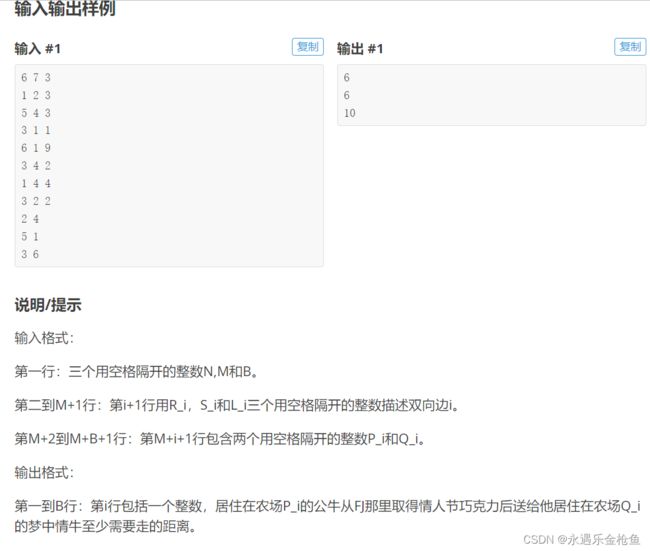
P2984 [USACO10FEB]Chocolate Giving S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
Farmer John有B头奶牛(1<=B<=25000),有N(2*B<=N<=50000)个农场,编号1-N,有M(N-1<=M<=100000)条双向边,第i条边连接农场R_i和S_i(1<=R_i<=N;1<=S_i<=N),该边的长度是L_i(1<=L_i<=2000)。居住在农场P_i的奶牛A(1<=P_i<=N),它想送一份新年礼物给居住在农场Q_i(1<=Q_i<=N)的奶牛B,但是奶牛A必须先到FJ(居住在编号1的农场)那里取礼物,然后再送给奶牛B。你的任务是:奶牛A至少需要走多远的路程?
这道题与上面那道题一模一样,小伙伴们可以自己尝试着做一下。
第四题(堆优化+有向边(max和min))
P2888 [USACO07NOV]Cow Hurdles S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目大意:Farmer John 想让她的奶牛准备郡级跳跃比赛,贝茜和她的伙伴们正在练习跨栏。她们很累,所以她们想消耗最少的能量来跨栏。 显然,对于一头奶牛跳过几个矮栏是很容易的,但是高栏却很难。于是,奶牛们总是关心路径上最高的栏的高度。 奶牛的训练场中有 N (1 ≤ N ≤ 300) 个站台,分别标记为1..N。所有站台之间有M (1 ≤ M ≤ 25,000)条单向路径,第i条路经是从站台Si开始,到站台Ei,其中最高的栏的高度为Hi (1 ≤ Hi ≤ 1,000,000)。无论如何跑,奶牛们都要跨栏。 奶牛们有 T (1 ≤ T ≤ 40,000) 个训练任务要完成。第 i 个任务包含两个数字 Ai 和 Bi (1 ≤ Ai ≤ N; 1 ≤ Bi ≤ N),表示奶牛必须从站台Ai跑到站台Bi,可以路过别的站台。奶牛们想找一条路径从站台Ai到站台Bi,使路径上最高的栏的高度最小。 你的任务就是写一个程序,计算出路径上最高的栏的高度的最小值。
输出:牛从起点到终点的路径上的最高的栏的高度的最小值,如果无法到达输出-1.
解析:这个题可以用floyd,花费时间137ms,不过这里讲的是dijkstra(497ms),所以就用dijkstra算法(mlogn=2 * 10 ^ 5)。这里的最短路就是栏的高度,上面求最短路都是用到方程:dis[j] = min(dis[j],dis[t]+f[t][j]);而这里用到的是dis[j] = min(dis[j], max(dis[t] , f[t][j])).我们用这个方程并套上面的模板去做该题,然后很理所应当地T掉,mlogn复杂度再乘T,可得时间复杂度8 * 10 ^ 9,严重超时。所以这题就没得做了吗?
当然不是。我们可以用二维d来存放一个点到另一个点的距离(记忆化),用vis来查看该点是否做过dijjkstra,不过这个好像更像bellman-ford,不过也没什么大碍,因为这两个算法在堆优化的时候是基本一样的。
#include
#include
#include
#include
#include
#define N 310
#define M 50010
#define inf 0x3f3f3f3f
using namespace std;
int n,m,T,cnt;
int ne[M],w[M],e[M],h[M],inque[N],d[N][N],vis[N];//用二维d来存储花费
//快读
inline int read() {
int date=0,w=1;
char c=getchar();
while(c<'0' || c>'9') {
if(c=='-') w=-1;
c=getchar();
}
while(c>='0' && c<='9') {
date=date*10+(c-'0');
c=getchar();
}
return date*w;
}
//邻接表
void add(int u,int v,int wi)
{
e[++cnt]=v;
w[cnt]=wi;
ne[cnt]=h[u];
h[u]=cnt;
}
void dijkstra(int s)
{
queueq;
memset(inque,0,sizeof(inque));
memset(d[s],inf,sizeof(d[s]));
q.push(s);
inque[s]=1;//先标记起点
d[s][s]=0;
while(!q.empty())
{
int u=q.front();
q.pop();
inque[u]=0;//取出来用就解除标记
for(int i=h[u]; i; i=ne[i])
{
int v=e[i];
if(d[s][v]>max(d[s][u],w[i]))
{
d[s][v]=max(d[s][u],w[i]);
if(!inque[v])
{
q.push(v);//进队就标记
inque[v]=1;
}
}
}
}
}
void print(int s,int t)
{
if(d[s][t]==inf)printf("-1\n");
else printf("%d\n",d[s][t]);
}
int main()
{
n=read(),m=read(),T=read();
for(int i=1;i<=m;i++)
{
int si=read(),ei=read(),hi=read();
add(si,ei,hi);
}
for(int i=1;i<=T;i++)
{
int ai=read(),bi=read();
if(!vis[ai]) dijkstra(ai);//判断是否以ai为起点走过
print(ai,bi);//输出,因为inf要输出-1,干脆写了个函数
vis[ai]=1;//记录以ai为起点走过了
}
return 0;
} 强烈建议小伙伴们好好消化完dijkstra的算法思想及掌握两个模板后,独立完成以上的例题,不要急于求成,直接看题解,这样做毫无意义可言。
希望我的文章能够对你有所启发,创作不易,希望你们能够动动小手点个赞,谢谢各位!