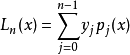数学建模学习笔记(5)初等数据处理方法
数据及其品质
1.提供数据
2.不提供数据 自己寻找可以反映问题本质的数据
3.问你需要什么数据 题目会提供一定的数据
4.需要自己判断应该采集什么数据才能说明什么事情
需要评估数据的精确性
分析数据时遇到的问题:
1.根据收集到的数据进行建模,要么数据有明显特征,要么插值
2.按照选出的一个或多个模型对数据进行拟合
3.从已经你和的模型中选取最合适的
观察法和初等数学方法
1.通过大量数据利用变量之间的比例性质得到自然规律(欧姆定律,万有引力定律,胡克定律等等)
2.观察法和初等数学方法相结合(参数方程,基本数学问题)
eg.将4条腿长相同的椅子放在不平的地上,怎么样才能放平?
问题分析:假定椅子中心不动,每条腿的着地点为ABCD,AC和BD的连线作为x.y轴,转动椅子看做坐标的旋转. 角α是旋转之后与初始位置的夹角。g(α)是AC旋转完与地面距离之和, f(α)表示BD两腿旋转之后与地面的距离之和,g和f都是连续函数,地面是一个连续的的曲面,由于三条腿总能同时着地(g=0或者f=0),所以g*f=0恒成立,则问题转化为:证明存在α使f=g=0
数据拟合方法
拟合和插值都是要求通过已知的观测数据去寻求某个近似函数,使得近似函数与已知数据有较高的拟合精度。
拟合:求过已知有限个数据点的近似函数,不要求过所有的数据点,只要求总偏差最小,反应基本趋势
插值:求过已知有限个数据点的近似函数,要求过每一个数据点
绝对偏差:数据点和拟合曲线之间的纵向偏差,拟合曲线上(Xi,Yi)与(Xi, f(Xi))之间距离之和最小
eg.测量直线段 AB=13 BC=7 AC=19 .这时AC应该是13+7=20而不是19 求各自的真值
设真值AB=x1 BC=x2 AC=x3=x1+x2 设残差r1=x1-13 r2=x2-7 r3=x3-19
则要指定r1 r2 r3的值使|r1| |r2| |r3|的最大者达到最小(Chebyshev准则)
记最大者是r 则要最小化r 约束条件 -r≤r1≤r -r≤r2≤r -r≤r3≤r
转化为经典数学线性规划问题:
r-x1+13≥0 (r-r1≥0)
r+x1-13≥0 (r+r1≥0)
r-x2+7≥0 (r-r2≥0)
r+x2-7≥0 (r+r2≥0)
r-x1-x2+19≥0 (r-r3≥0)
r+x1+x2-19≥0 (r+r3≥0)
总结:
数据拟合有三种判别准则:偏差的绝对值之和最小、偏差的最大绝对值最小、偏差的平方和最小(最小二乘法)。
插值方法
插值函数:已知某未知函数y=f(x)(不知道具体表达式)的一组观测数据(xi,yi),求一个φ(x)使φ(xi)=yi,则φ(x)≈f(x),φ(x)是f(x)的插值函数。xi为插值结点,φ(xi)=yi为插值条件。
1.拉格朗日插值法点击打开链接
插值多项式:已知函数y=f(x)上x0 x1 x2.......xn等n+1个不同的点对应的函数值为y0 y1 y2 .......yn,要求一个次数不超过n的多项式pn(x)=a0+a1x+a2x^2+........+anx^n使得在xi上有pn(xi)=yi。
只要n+1个插值节点xo x1 x2.....xn互异,满足插值条件的插值多项式就唯一存在。
Rn(x)=f(x)-pn(x)为pn(x)的截断误差/插值余项。
思考:
回顾带拉格朗日余项的Taylor公式,其中的Taylor多项式与n次拉格朗日插值多项式有什么区别?
2.牛顿插值法点击打开链接
函数的差商:给定函数
可将k阶差商 表示为函数值 的组合:
牛顿插值公式:
![]()
![]()
每增加一个节点插值多项式只增加一项,便于计算
记为:![]() 其中,
其中,
3.Hermitc插值法点击打开链接
4.分段线性插值法:
将每两个相邻的节点用直线连接起来形成的一条折线,就是分段线性插值函数 In(x)
计算量与节点的个数无关,n越大,分段越多,误差越小 但是不够光滑
5.样条插值法点击打开链接
这一章可以说是非常懒了 公式好复杂也不想一个一个打 记也记不住 嘛~好累额