深大算法实验五——桥
代码链接:深大算法实验五——查找所有的桥-C++文档类资源-CSDN下载
目录
问题描述:
实验要求
一.桥的定义
二.求解问题
三.实现算法:
1. 存储数据结构
2.基准算法:
3. 改进的基准算法
4. 使用边生成并查集树边进行LCA算法
5. LCA+路径压缩方法
数据分析:
基准算法:
实验结论:
问题描述:
1. 桥的定义
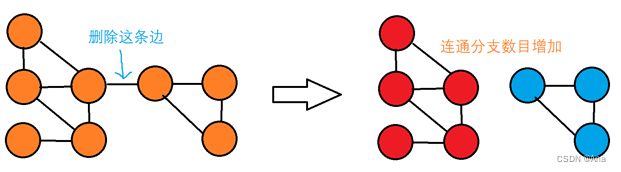
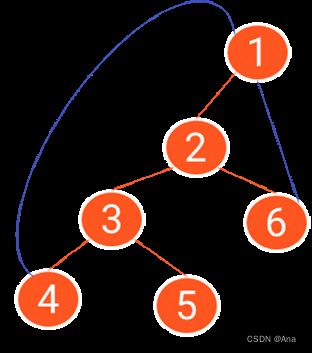
在图论中,一条边被称为“桥”代表这条边一旦被删除,这张图的连通块数量会增加。等价地说,一条边是一座桥当且仅当这条边不在任何环上。一张图可以有零或多座桥。
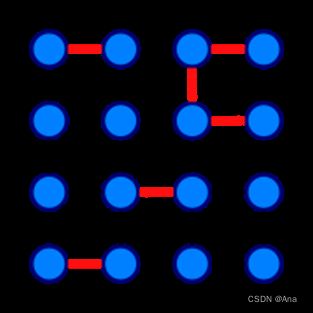
图 1 没有桥的无向连通图 图 2 这是有16个顶点和6个桥的图
(桥以红色线段标示)
2. 求解问题
找出一个无向图中所有的桥。
实验要求
- 实现上述基准算法。
- 设计的高效算法中必须使用并查集,如有需要,可以配合使用其他任何数据结构。
- 用图2的例子验证算法正确性。
- 使用文件 mediumG.txt和largeG.txt 中的无向图测试基准算法和高效算法的性能,记录两个算法的运行时间。
- 设计的高效算法的运行时间作为评分标准之一。
- 提交程序源代码。
- 实验报告中要详细描述算法设计的思想,核心步骤,使用的数据结构。
一.桥的定义
在图论中,一条边被称为“桥”代表这条边一旦被删除,这张图的连通块数量会增加。等价地说,一条边是一座桥当且仅当这条边不在任何环上。一张图可以有零或多座桥。
二.求解问题
找出一个无向图中所有的桥。
三.实现算法:
1. 存储数据结构
由于图的存储方式有两种,一个是邻接表,另外一个是邻接矩阵。邻接矩阵有实现简单,用于矩阵运算时方便等特点,但是本次算法不需要进行矩阵的运算,且需要使用到深度优先遍历,所以本次实验存储图的方式是使用邻接表的形式进行存储。
在使用邻接表进行存储时,DFS的时间复杂度是![]() ,而在使用邻接矩阵进行存储的话,DFS的时间复杂度是
,而在使用邻接矩阵进行存储的话,DFS的时间复杂度是![]() ,所以说用邻接矩阵存储效率是更高的。
,所以说用邻接矩阵存储效率是更高的。
因为实验中有删除边或者加入边的操作,所以同时也将边存储在一个数组当中。
邻接表的形成我是是用了一个二维数组,由于每一个节点都是按顺序的,数组的第一个标志就代表一个节点,后面的代表与他相连接的节点。
2.基准算法:
基准算法的思想是十分简单的,实际上就是先将图按照遍历一边找到有多少个连通分量,再将每一个边进行删除,再次遍历该图,检查联通分量是否有增加。
伪代码:
Standard (edge, edgeNum, Bridge)
conNum=DFS()
for i = 0 to edgeNum
Delete(edge[i])
DelNum = DFS()
if (DelNum > conNum)
Bridge.add(edge[i])
这种算法实现简单但是十分的消耗时间,所以是不太推荐使用的。
算法效率是:![]()
3. 改进的基准算法
若一个图有很多的连通子图,那么上述删除边后,会遍历到不在这个边上的连通图。
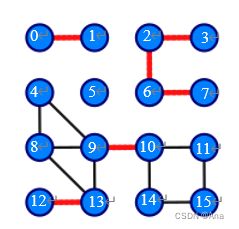
例如下图,
节点0和1是一个连通图,当他们的边被删除后,若使用没有改进的基准算法,则还要遍历其他没有用的连通图,这大大降低了效率。
改进的算法是先将该图分离成各个连通子图,然后在删除相应边的连通子图上进行遍历,检查是否能够经过一次深度优先遍历访问到所有的节点,如果无法遍历到所有的节点,则说明这是一个桥,并记录。
当连通子图数量很多的时候,使用这个算法会比普通基准算法的效率要高很多,方式连通子图很少或者图本身是一个连通图时,则这个改进算法并不能提高很多的效率。
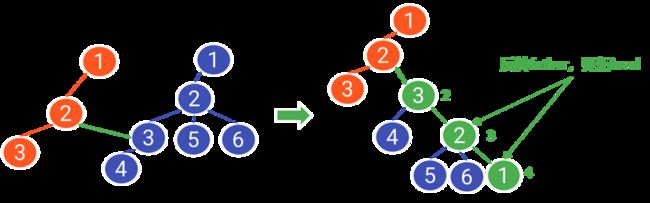
4. 使用边生成并查集树边进行LCA算法
该算法的主要思想是先不产生一个图的邻接表,先将每个节点视为一颗树。当访问一条边时,将相应的节点进行连接,也就是Union操作,并且更新新的树上的数据。
树的存储由数组存储,并且有5个数据,分别是Father,记录该节点连接的上一个节点编号。Head,该节点所在的树的树根节点编号。Level,属于这个数的第几层。Next,记录下该节点下一个节点,用数组存储。Num,代表这棵树有多少个节点。
并查集生成树时,总共会有三种情况:①:一个节点在树中,另外一个节点是单一节点。②:两个节点分别在两颗不同的树中。③:两个节点在同一颗树中。
情况①:此时只需要将单独的节点加入到对应节点,并且更新该节点的数据即可。
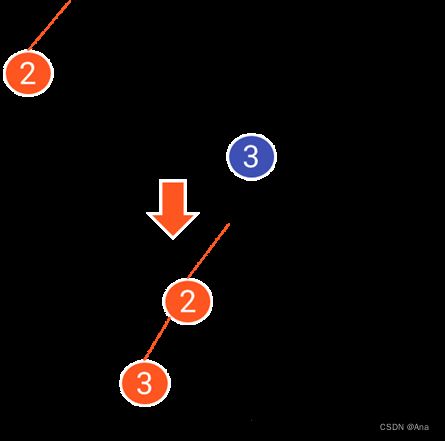
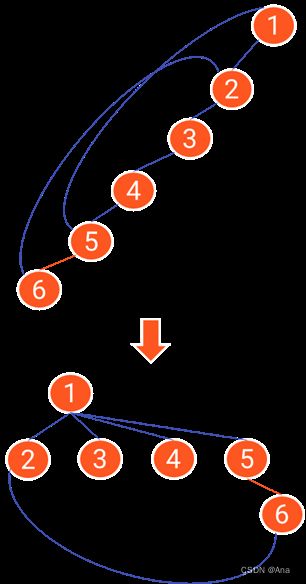
情况②:这种情况有些许麻烦,如图所示,
首先将这两个节点进行连接,向上寻找头节点并且将遍历过程中的节点的father和next进行反转,并且运用DFS来进行对新增的树的head和level进行更新。
为了地高效率,则要将节点数少的树连接道节点数多的树当中,所以在最开始的时候要判断哪一颗树的节点数大。
情况③:当两个两个节点都在同一颗树上时,则说明这条边不是桥,并且要将树当中的环边进行删除。
如图所示,当加入(1,4)这条边时,这两个节点都在同一颗树上,则选择Level值大的节点进行向上的遍历,一直遍历到与另一个节点的level值相同,此时两个节点同时向上遍历,直到遍历到两个相同的节点。此时所遍历到的节点所对应的边都是属于环遍,要将其从桥边的数据中删除。
接着对该树进一步的优化,也就是路径压缩:
如图,(1,5)这条边是之前所检测的环边,则说明1,2,3,4,5所对应的边都是属于环边,当再一次进行删除环边操作时都会指向同一节点——1节点。但是如果做路径压缩的话,当再加入一个环边进行遍历时(如加入边(2,6))则遍历的次数要多。
路径压缩就是将所遍历的节点全部存储到刚刚同时遍历到的节点处,此图就是将遍历到的2,3,4,5节点放到了共同节点1下面。
当此图加入(2,6)边时,若没有进行路径压缩,则需要进行5次遍历,若进行了路径压缩,则只需要遍历3次,明显次数变少。
这种算法使用到了并查集生成树,可以更加快速的判断条边是否的是环遍,但是也存在一些相应的问题,由于每次union都有可能进行一次对数据更新的DFS操作,所以当数据很大且树逐渐变大之后,速度会越来越慢。
5. LCA+路径压缩方法
该算法与上一个算法的思路是差不多的,只不过该算法是先生成生成树,在进行对环遍减去。
先将数据用邻接表进行存储,并且用DFS深度优先遍历生成一颗生成树,并且按照上述算法一样找到环边并对路径压缩。
在路径压缩时由于要更新节点的level值所以也会使得算法效率十分的缓慢,那么是否有方法可以不用更新level值也可以实现该操作呢?
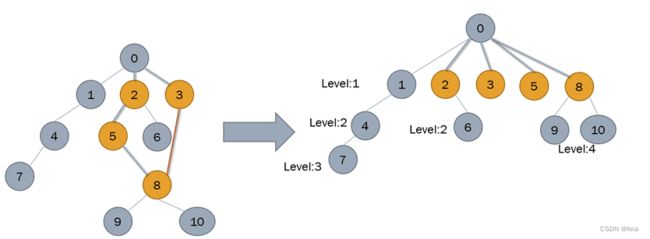
实际上当路径压缩后,可以不更新level值,因为当有一个节点是在更新后的节点后面时,肯定要经过更新过后的节点,只是在向上遍历的时候要每一次判断哪一个节点的level值更大。如图所示。
当边(3,8)进行连接时,那么经过路径压缩后则会变成右图,右边黄色的节点的Level值全部都为1,但是在路径压缩后节点9和10的Level值没有更新,还是保持原来的Level为4。那么下一次连接(7,9)节点时,因为节点9的Level值比系欸但7的Level值大,所以先是节点9向上遍历,但当向上遇到节点8时,8的Level是1,比节点7的Level值小,此时就转换,让节点7向上遍历,直到遍历到节点1与系欸但8的Level值相等的情况下,两边的节点再同时向上遍历到共同节点。
找到环边以后,我们先记录下环边,等到所有环边被找到后再进行统一的删除。
以上是找环边的操作,同样的自旋边和重复边也可以按照这个算法进行。
数据分析:
基准算法:
经过优化后的基准算法跑mediumDG数据集时只需要用0.094秒,但是跑largeG数据集时需要消耗很多的时间,基本上跑不出来。
同样的使用边生成并查集树边进行LCA操作跑mediumDG需要0.075秒,但是依旧无法跑largeG数据集,这是因为每次加一颗树的时候都要进行一次DFS,这明显使得时间降低了。
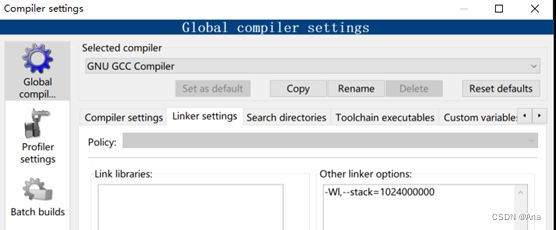
对于先进行DFS生成树在进行LCA的算法,mediumDG只需要0.064秒,但是当我跑largeG数据集时或发生错误,后面到网上查找资料这是因为编译器的栈空间不足导致的,查阅网上资料后我将CodeBlocks的IDE的栈空间进行了扩展,就可以跑数据集了。
DFS生成树再进行LCA的算法,largeG数据集只需要20.282秒就可以跑出来。
实验结论:
本次实验我所用的时间比较久,我一开始使用边生成树边进行LCA找环边的算法,但是这种算法在运行largeG时十分的缓慢,所以后面我又是用了先生成树在进行lca找环边的算法,这样可以跑出数据集但还是不是特别的快速。
本次实验理解并且实现了图的算法和数据结构,对图这种数据结构有了更深层次的理解。