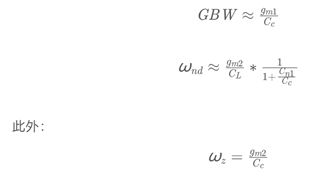【模拟IC】二级运放设计的关键点——GBW与PM！

本章接下来的内容，将着重介绍如何得到要求的GBW与PM，同学们可以参照对比sansen第五、六章学习，但抛开课本，也完全可以理解本部分的内容。我们会将重点放在如何通过给定的指标——相位裕度以及GBW，得到合适的小信号参数——第一级跨导gm1、第二级跨导gm2以及密勒补偿电容Cc，而抛开诸如“开环频率响应与闭环频率响应的关系”、“为什么需要70°的相位裕度，频率响应才能完全没有尖峰”以及“频率特性与其他指标如何折中”等问题。

以上被我们忽略的问题，事实上都及其重要，但我相信第一次接触运放设计的同学们，比起“尽善尽美”地掌握所有运放设计理论，更关心如何快速上手，即如何满足设计指标。因此，在本节内容中，我们只需要关心，我们如何得到60°的相位裕度，以及100MHz的GBW，而无需关心这些指标为什么是这样，满足这样的指标又意味着适用于哪些应用。

接下来，笔者将贯通全章，通过分步骤的方式，带领同学们一步步从给定的相位裕度、GBW，得到合适的设计参数。

Step 1 指标分析与转化

首先需要明确的是，由于我们引入的运放环境，是单位增益负反馈，因此反馈系数F=1，则环路增益LG可以表示为：

其中Aopen为运放的开环增益。

也就是说，反馈系统环路增益的频率响应，与运放本身开环的频率响应几乎一致，只有相位上存在180°的区别。因此，在以下的分析中，我们采用运放的开环频率响应，代替环路增益的频率响应。

我们接下来，把目光放在GBW与PM。在这两个指标中，GBW是相对容易理解与分析的一个，即增益与带宽的乘积，也可以理解为单位增益带宽，直接与运放传输函数中的极零点相关联。

而相位裕度这一指标则不那么直观，我们首先要将“相位裕度大于60°”这一要求，转化为对极零点位置的要求。

首先，我们知道，这个电路存在一个主极点——由Cc的密勒效应引入，一个次极点——由负载电容CL引入，以及一个正零点——由Cc的前馈效应引入。

在这里我们忽略了由节点A引入的一个极零点对，因为这一节点的寄生电容引入的零点位于它引入的极点的二倍处，且该零点为负零点，可以很大程度上补偿自身引入的极点，因此我们认为这一极零点对频率响应影响较小。但由于极点在零点之前，因此我们这里给这一因素留有设计裕量，认为这一极零点对“吃掉”了5°的PM，而忽略这一对极零点对频率响应的其他影响。

零极点定性分析与Bode图示意：

基于以上分析，二级运放的频率响应可以被描述为：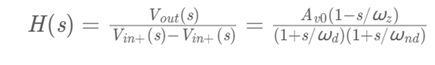
其中，Av0为直流增益，ωz为零点，ωd为主极点，ωnd为次主极点。我们在这里先不讨论这些极零点具体的表达式。
相位裕度大于60°，也就意味着，将s=j*GBW代入H(s)的表达式，其相位∠H(s)应大于-120°，即：

去掉负号后：

由于GBW等于直流增益Av0与主极点ωd为主极点的乘积，而Av0通常足够大，所以其的

我们认为约等于90°。因此有：

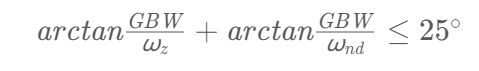
现在只剩下一个零点与一个次主极点，而零点在设计中，由于其频率较高，通常对相位裕度的影响小于次主极点，因此我们只给零点带来的相移留8°的余量，则有：

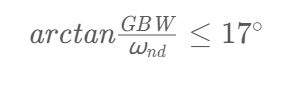
那么我们就可以得到ωnd与GBW的关系：

在这里我们留有余量，则认为次主极点ωnd应至少为GBW的4倍。同时：

那么我们就可以得到ωz与GBW的关系：

在这里我们留有余量，则认为ωz应至少为GBW的8倍。

至此，我们将相位裕度的要求，转化为了次主极点ωnd、ωz与GBW的关系，更有利于我们对二级运放进行直观的设计。

---

Step 2 零极点计算

在明确了对极零点的要求后，我们还需要用二级运放中的小信号设计参数——gm1、gm2以及Cc，来写出极零点的表达式。
首先，我们画出差分小信号模型图：

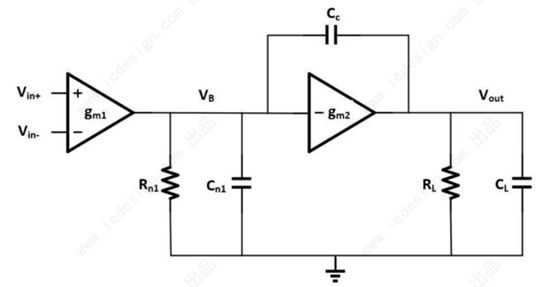
其中：
Rn1为第一级的输出阻抗，由M1与M4的输出阻抗并联构成；

Cn1为第一级输出节点对地的寄生电容（不包含补偿电容的密勒效应），由M1、M4的漏极电容以及M2的栅极电容构成；

RL为第二级的输出阻抗，由第二级的两个管子——M2、M6的输出电阻并联组成；

CL为二级运放的负载电容，由指标决定为1pF，会被M2、M6的漏极电容略微影响。

在这里，我们将第一、二级等效为两个gm单元，大小分别等于M1管的gm1与M2管的gm2。
然后，我们可以进一步简化我们的小信号模型图：

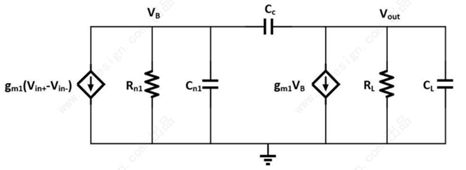
在之后的篇幅中，我们都采用这个小信号模型，对差分小信号进行分析计算。

得到了小信号模型，我们就可以通过计算，得到这个小信号电路的零极点。

我们在这里总结了ωnd与GBW的简化形式，在后续的分析中，我们采用以下的表达式，在方便设计的同时，保证了准确性：