推荐模型——逻辑回归
文章目录
- 1. 逻辑回归特点
- 2. 基于逻辑回归的推荐流程
- 3. 逻辑回归模型的数学形式
- 4. 逻辑回归模型的训练方法
- 5. 逻辑回归模型的优势
-
- 5.1 数学含义上的支撑
- 5.2 可解释性强
- 5.3 工程化的需要
- 6. 逻辑回归的局限性
1. 逻辑回归特点
- 逻辑回归是融合多种特征的推荐模型。
相比于协同过滤模型仅利用用户与物品的相互行为信息进行推荐,逻辑回归模型能够综合利用用户、物品、上下文等多种不同的特征,生成较为“全面”的推荐结果。另外,逻辑回归的另一种表现形式"感知机"作为神经网络中最基础的单一神经元,是深度学习的基础性结构 。 因此,能够进行多特征融合的逻辑回归模型成了独立于协同过滤的推荐模型发展的另一个主要方向 。
相比于协同过滤和矩阵分解利用用户和物品的“相似度”进行推荐,逻辑回归将推荐问题看成一个分类问题,通过预测正样本的的概率对物品进行排序。这里的正样本可以使用户“点击”了某商品,也可以是用户“观看”了某视频,均是推荐系统希望用户产生“正反馈”行为。因此,逻辑回归模型将推荐问题转换成一个点击率(Click Through Rate,CTR)预估问题。
2. 基于逻辑回归的推荐流程
(1) 将用户年龄、性别、物品属性、物品描述、当前时间、当前地点等特征转换成数值型特征向量。
(2) 确定逻辑回归模型的优化目标(以优化“点击率”为例),利用已有样本数据对逻辑回归模型进行训练,确定逻辑回归模型的内部参数。
(3) 在模型服务阶段,将特征向量输入逻辑回归模型,经过逻辑回归模型的推荐,得到用户“点击”(这里用点击作为推荐系统正反馈行为的例子)物品的概率。
(4) 利用“点击”概率对所有候选物品进行排序,得到推荐列表。
利用逻辑回归的推荐过程的重点在于,利用样本的特征向量进行模型训练和在线推断。
下面着重介绍逻辑回归模型的数学形式、推断过程、训练方法。
3. 逻辑回归模型的数学形式
如图所示,逻辑回归模型的推断过程可以分为如下几步:
对于标准的逻辑回归模型来说,要确定的参数就是特征向量相应的权重向量 w, 下面介绍逻辑回归模型的权重向量 w 的训练方法 。
4. 逻辑回归模型的训练方法
逻辑回归模型常用的训练方法是梯度下降法、牛顿法、拟牛顿法,其中梯度下降法是应用最广泛的训练方法,也是深度学习各种训练方法的基础。
- 简单介绍梯度下降法:
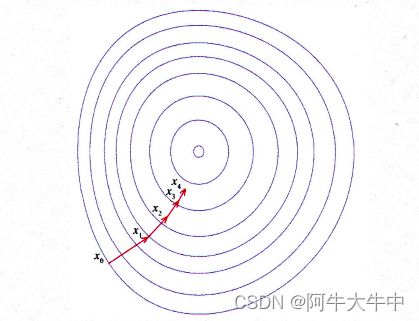
梯度下降法是一个一阶最优化算法。应用梯度下降法的目的是找到一个函数的局部极小值。为此,必须沿函数上当前点对应梯度(或者是近似梯度)的反方向进行规定步长距离的迭代搜索。如果向梯度正方向进行搜索,则会接近函数的局部极大值点,这个过程被称为梯度上升法。
梯度下降法很像寻找一个盆地最低点的过程 。 那么,在寻找最低点的过程中,沿哪个方向才是下降最快的方向呢?
这就利用了“梯度”的性质:如果实值函数F(x)在点x0处可微且有定义,那么函数F(x)在点x0处沿着梯度相反的方向-▽F(x)下降最快。
因此,在优化某模型的目标函数时,只需要对魔表函数进行求导,得到梯度的方向,沿梯度的反方向下降,并迭代此过程直到寻找到局部最小点。
使用梯度下降法求解逻辑回归模型的第一步是确定逻辑回归的目标函数。已知逻辑回归的数学形式如:
这里表示成:
对于一个输入样本x,预测结果为正样本(类别1)和负样本(类别0)的概率:
可以将上式写成:
由极大似然估计的原理可以写出逻辑回归的目标函数:
由于目标函数连乘形式不便于求导,故两侧取log,并乘以系数-(1/m),将求最大值的问题转换成求极小值的问题,最终的目标函数:
得到逻辑回归的目标函数后,需要对每个参数求偏导,得到梯度方向:
在得到梯度之后,即可得到模型参数的更新公式:
至此,完成了逻辑回归模型的更新推导。
5. 逻辑回归模型的优势
在深度学习模型流行之前,逻辑回归模型曾在相当长的一段时间里是推荐系统、计算广告业界的主要选择之一。除了在形式上适于融合不同特征,形成较“全面”的推荐结果,其流行的原因还有三个方面:①数学含义上的支撑;②可解释性强;③工程化的需要。
5.1 数学含义上的支撑
逻辑回归作为广义线性模型的一种,它的假设是因变量y服从伯努利分布 。 那么在CTR预估这个问题上,"点击"事件是否发生就是模型的因变量 y, 而用户是否点击广告是一个经典的掷偏心硬币问题。 因此, CTR模型的因变量显然应该服从伯努利分布。所以,采用逻辑回归作为 CTR 模型是符合"点击"这一事件的物理意义的 。
与之相比,线性回归作为广义线性模型的另一特例,其假设是因变量y服从高斯分布,这明显不是点击这类二分类问题的数学假设 。
5.2 可解释性强
直观地说,逻辑回归模型的数学形式是各特征的加权和,再施以sigmoid函数。在逻辑回归数学基础的支撑下,逻辑回归的简单数学形式业非常符合人类对预估直觉认知。
使用各种特征的加权是为了综合不同特征对CTR的影响,而不同的特征的重要程度不同,所以为不同特征制定不同的权重,代表不同的重要程度。最后,通过sigmoid函数,使其能够映射到0~1区间,正好符合CTR的物理意义。
逻辑回归如此符合人类的直觉认知显然有其他的好处——使模型具有极强的可解释性。算法工程师可以轻易地根据权重的不同解释那些特征比较重要,在CTR模型的预测有偏差时定位是哪些因素影响了最后的结果。在与负责运营、产品的同事合作时,也便于给出可解释性的原因,有效降低沟通成本。
5.3 工程化的需要
在互联网公司每天动辄 TB 级别的数据面前,模型的训练开销和在线推断效率显得异常重要 。 在 GPU 尚未流行的 2012 年之前,逻辑回归模型凭借其易于并行化、模型简单、训练开销小等特点,占据着工程领域的主流 。 圄于工程团队的限制,即使其他复杂模型的效果有所提升,在没有明显击败逻辑回归模型之前, 公司也不会贸然加大计算资源的投入,升级推荐模型或 CTR 模型,这是逻辑回归持续流行的另一重要原因 。
6. 逻辑回归的局限性
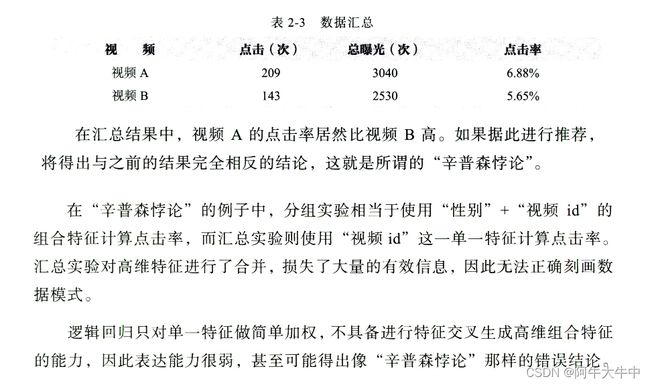
逻辑回归模型表达能力不强的问题,会不可避免地造成有效信息的损失。 在仅利用单一特征而非交叉特征进行判断的情况下,有时不仅是信息损失的问题, 甚至会得出错误的结论。 著名的"辛普森悖论"用 一个 非常简单的例子,说明了进行多维度特征交叉的重要性。
介绍“辛普森悖论”:
在对样本集合进行分组研究时,在分组比较中都占优势的一方,在总评中有时反而是失势的一方,这种有悖常理的现象 ,被称为" 辛普森悖论" 。 下面用一个视频推荐的例子进一步说明什么是"辛普森悖论"。
因此,通过改造逻辑回归模型,使其具备特征交叉的能力是必要和迫切的 。