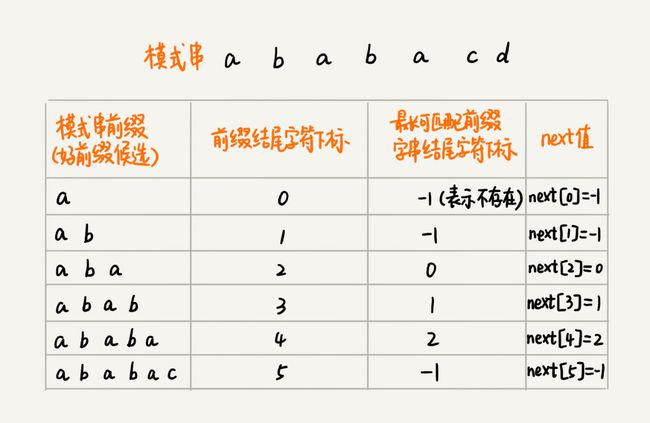
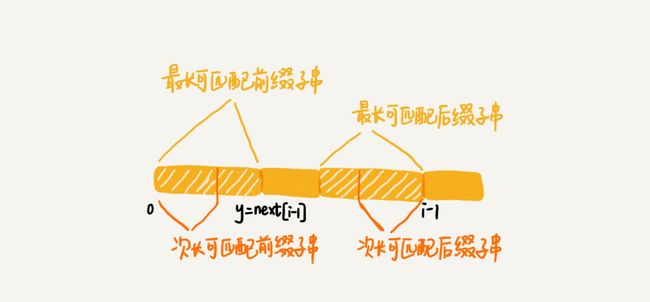
- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- Goolge earth studio 进阶4——路径修改与平滑
陟彼高冈yu
Googleearthstudio进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径,所以当我们通过这个关键帧时,不是一个生硬的角度,而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄,允许我们调整路径的形状。右键单击,我们可以选择“平滑路径”,这是默认的自动平滑算法,或者我们可
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- 121. 买卖股票的最佳时机
薄荷糖的味道_fb40
给定一个数组,它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天(股票价格=1)的时候买入,在第5天(股票价格=6)的时候卖出,最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
- 每日算法&面试题,大厂特训二十八天——第二十天(树)
肥学
⚡算法题⚡面试题每日精进java算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题,最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧!!特别介绍小白练手专栏,适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
- 回溯算法-重新安排行程
chirou_
算法数据结构图论c++图搜索
leetcode332.重新安排行程这题我还没自己ac过,只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多,用什么数据结构去存数据,去读取数据,都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
- Faiss:高效相似性搜索与聚类的利器
网络·魚
大数据faiss
Faiss是一个针对大规模向量集合的相似性搜索库,由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构,用于加速向量之间的相似性搜索,特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理:近似最近邻搜索:Faiss的核心功能之一是近似最近邻搜索,它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的,
- insert into select 主键自增_mybatis拦截器实现主键自动生成
weixin_39521651
insertintoselect主键自增mybatisdelete返回值mybatisinsert返回主键mybatisinsert返回对象mybatisplusinsert返回主键mybatisplus插入生成id
前言前阵子和朋友聊天,他说他们项目有个需求,要实现主键自动生成,不想每次新增的时候,都手动设置主键。于是我就问他,那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成,因此为了项目稳定性,不会切换id的生成方式。朋友问我有没有什么实现思路,他们公司的orm框架是mybatis,我就建议他说,不然让你老大把mybatis切换成mybatis-plus。mybat
- k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题)
寻找你83497
k均值聚类算法考试例题
?算法:第一步:选K个初始聚类中心,z1(1),z2(1),…,zK(1),其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定,例如可选开始的K个.k均值聚类:---------一种硬聚类算法,隶属度只有两个取值0或1,提出的基本根据是“类内误差平方和最小化”准则;模糊的c均值聚类算法:--------一种模糊聚类算法,是.K均值聚类算法是先随机选取K个对象作为初始的聚类
- Python实现简单的机器学习算法
master_chenchengg
pythonpython办公效率python开发IT
Python实现简单的机器学习算法开篇:初探机器学习的奇妙之旅搭建环境:一切从安装开始必备工具箱第一步:安装Anaconda和JupyterNotebook小贴士:如何配置Python环境变量算法初体验:从零开始的Python机器学习线性回归:让数据说话数据准备:从哪里找数据编码实战:Python实现线性回归模型评估:如何判断模型好坏逻辑回归:从分类开始理论入门:什么是逻辑回归代码实现:使用skl
- 推荐算法_隐语义-梯度下降
_feivirus_
算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵,值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
- K近邻算法_分类鸢尾花数据集
_feivirus_
算法机器学习和数学分类机器学习K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
- 数据结构 | 栈和队列
TT-Kun
数据结构与算法数据结构栈队列C语言
文章目录栈和队列1.栈:后进先出(LIFO)的数据结构1.1概念与结构1.2栈的实现2.队列:先进先出(FIFO)的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中,栈和队列是两种基本且重要的数据结构,它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
- [Python] 数据结构 详解及代码
AIAdvocate
算法python数据结构链表
今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
- Python算法L5:贪心算法
小熊同学哦
Python算法算法python贪心算法
Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点:缺点:结语贪心算法(GreedyAlgorithm)是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是,在保证每一步局部最优的情况下,希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
- 【RabbitMQ 项目】服务端:数据管理模块之绑定管理
月夜星辉雪
rabbitmq分布式
文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字:交换机的路由交换算法中会用到没有是否持久化的标志,因为绑定是否持久化取决于交换机和队列是否持久化,只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子,两端连接着交换机和队列,当一方不存在,它就没有存在的必要了定义绑定持久化类构造函数:如果数据库文件不存在则创建,打开数据库,创建binding_table插入
- 非对称加密算法原理与应用2——RSA私钥加密文件
私语茶馆
云部署与开发架构及产品灵感记录RSA2048私钥加密
作者:私语茶馆1.相关章节(1)非对称加密算法原理与应用1——秘钥的生成-CSDN博客第一章节讲述的是创建秘钥对,并将公钥和私钥导出为文件格式存储。本章节继续讲如何利用私钥加密内容,包括从密钥库或文件中读取私钥,并用RSA算法加密文件和String。2.私钥加密的概述本文主要基于第一章节的RSA2048bit的非对称加密算法讲述如何利用私钥加密文件。这种加密后的文件,只能由该私钥对应的公钥来解密。
- 粒子群优化 (PSO) 在三维正弦波函数中的应用
subject625Ruben
机器学习人工智能matlab算法
在这篇博客中,我们将展示如何使用粒子群优化(PSO)算法求解三维正弦波函数,并通过增加正弦波扰动,使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程,并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数,定义如下:objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
- 非对称加密算法————RSA理论及详情
hu19930613
转自:https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前,所有的加密方法都是同一种模式:(1)甲方选择某一种加密规则,对信息进行加密;(2)乙方使用同一种规则,对信息进行解密。由于加密和解密使用同样规则(简称"密钥"),这被称为"对称加密算法"(Symmetric-keyalgorithm)。这种加密模式有一个最大弱点
- ai绘画工具midjourney怎么下载?附作品管理教程
设计师早上好
Midjourney是一款功能强大的AI绘画工具,它使用机器学习技术和深度神经网络等算法,可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么,ai绘画工具midjourney怎么下载?本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单,只需打开Midjourney官网(点击“GetMidjour
- 【加密算法基础——对称加密和非对称加密】
XWWW668899
网络安全服务器笔记
对称加密与非对称加密对称加密和非对称加密是两种基本的加密方法,各自有不同的特点和用途。以下是详细比较:1.对称加密特点密钥:使用相同的密钥进行加密和解密。发送方和接收方必须共享这个密钥。速度:通常速度较快,适合处理大量数据。实现:算法相对简单,计算效率高。常见算法AES(高级加密标准)DES(数据加密标准)3DES(三重数据加密标准)RC4(流密码)应用场景文件加密磁盘加密传输大量数据时的加密2.
- 【算法练习】IDEA集成leetcode插件实现快速刷
2401_84102892
2024年程序员学习算法intellij-idealeetcode
============点击右侧边leetcode->设置->配置地址、用户名、密码、存放目录、文件模板用户名要登录后在账号信息里看模板代码1.codefilename!velocityTool.camelC
- 【加密算法基础——RSA 加密】
XWWW668899
网络服务器笔记python
RSA加密RSA(Rivest-Shamir-Adleman)加密是非对称加密,一种广泛使用的公钥加密算法,主要用于安全数据传输。公钥用于加密,私钥用于解密。RSA加密算法的名称来源于其三位发明者的姓氏:R:RonRivestS:AdiShamirA:LeonardAdleman这三位计算机科学家在1977年共同提出了这一算法,并发表了相关论文。他们的工作为公钥加密的基础奠定了重要基础,使得安全通
- 机器学习-聚类算法
不良人龍木木
机器学习机器学习算法聚类
机器学习-聚类算法1.AHC2.K-means3.SC4.MCL仅个人笔记,感谢点赞关注!1.AHC2.K-means3.SC传统谱聚类:个人对谱聚类算法的理解以及改进4.MCL目前仅专注于NLP的技术学习和分享感谢大家的关注与支持!
- 生成式地图制图
Bwywb_3
深度学习机器学习深度学习生成对抗网络
生成式地图制图(GenerativeCartography)是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统(GIS)技术与现代生成模型(如深度学习、GANs等),能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点:自动化生成:通过算法和模型,系统能够根据输入的地理或空间数据自动生成地图,而无需人工逐
- 高性能javascript--算法和流程控制
海淀萌狗
-for,while和do-while性能相当-避免使用for-in循环,==除非遍历一个属性量未知的对象==es5:for-in遍历的对象便不局限于数组,还可以遍历对象。原因:for-in每次迭代操作会同时搜索实例或者原型属性,for-in循环的每次迭代都会产生更多开销,因此要比其他循环类型慢,一般速度为其他类型循环的1/7。因此,除非明确需要迭代一个属性数量未知的对象,否则应避免使用for-i
- 深度 Qlearning:在直播推荐系统中的应用
AGI通用人工智能之禅
程序员提升自我硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLMJavaPython架构设计Agent程序员实现财富自由
深度Q-learning:在直播推荐系统中的应用关键词:深度Q-learning,强化学习,直播推荐系统,个性化推荐1.背景介绍1.1问题的由来随着互联网技术的飞速发展,直播平台如雨后春笋般涌现。面对海量的直播内容,用户很难快速找到自己感兴趣的内容。因此,个性化推荐系统在直播平台中扮演着越来越重要的角色。1.2研究现状目前,主流的个性化推荐算法包括协同过滤、基于内容的推荐等。这些方法在一定程度上缓
- JVM源码分析之堆外内存完全解读
HeapDump性能社区
概述广义的堆外内存说到堆外内存,那大家肯定想到堆内内存,这也是我们大家接触最多的,我们在jvm参数里通常设置-Xmx来指定我们的堆的最大值,不过这还不是我们理解的Java堆,-Xmx的值是新生代和老生代的和的最大值,我们在jvm参数里通常还会加一个参数-XX:MaxPermSize来指定持久代的最大值,那么我们认识的Java堆的最大值其实是-Xmx和-XX:MaxPermSize的总和,在分代算法
- 《算法》四学习——1.1节
进阶的Farmer
算法算法笔记
前言买了一本算法4,每天看一点,对每个小结来个学习总结,输出驱动输入。本篇笔记针对第一章基础1.1基础编程模型1.1节总结了相关的语法、语言特性和书中将会用到的库。笔记自己在编码中容易遗漏的点&&优先级比||高在开发中习惯了加括号,所以没注意到这点,教材上也有但是忘记了二分查找中计算mid=left+(right-left)/2这样计算可以有效避免(left+right)/2溢出答疑java无穷大
- 排序
路小白同学
1.冒泡排序冒泡算法是一种基础的排序算法,这种算法会重复的比较数组中相邻的两个元素。如果一个元素比另一个元素大(小),那么就交换这两个元素的位置。重复这一比较直至最后一个元素。这一比较会重复n-1趟,每一趟比较n-j次,j是已经排序好的元素个数。每一趟比较都能找出未排序元素中最大或者最小的那个数字。这就如同水泡从水底逐个飘到水面一样。冒泡排序是一种时间复杂度较高,效率较低的排序方法。其空间复杂度是
- Spring中@Value注解,需要注意的地方
无量
springbean@Valuexml
Spring 3以后,支持@Value注解的方式获取properties文件中的配置值,简化了读取配置文件的复杂操作
1、在applicationContext.xml文件(或引用文件中)中配置properties文件
<bean id="appProperty"
class="org.springframework.beans.fac
- mongoDB 分片
开窍的石头
mongodb
mongoDB的分片。要mongos查询数据时候 先查询configsvr看数据在那台shard上,configsvr上边放的是metar信息,指的是那条数据在那个片上。由此可以看出mongo在做分片的时候咱们至少要有一个configsvr,和两个以上的shard(片)信息。
第一步启动两台以上的mongo服务
&nb
- OVER(PARTITION BY)函数用法
0624chenhong
oracle
这篇写得很好,引自
http://www.cnblogs.com/lanzi/archive/2010/10/26/1861338.html
OVER(PARTITION BY)函数用法
2010年10月26日
OVER(PARTITION BY)函数介绍
开窗函数 &nb
- Android开发中,ADB server didn't ACK 解决方法
一炮送你回车库
Android开发
首先通知:凡是安装360、豌豆荚、腾讯管家的全部卸载,然后再尝试。
一直没搞明白这个问题咋出现的,但今天看到一个方法,搞定了!原来是豌豆荚占用了 5037 端口导致。
参见原文章:一个豌豆荚引发的血案——关于ADB server didn't ACK的问题
简单来讲,首先将Windows任务进程中的豌豆荚干掉,如果还是不行,再继续按下列步骤排查。
&nb
- canvas中的像素绘制问题
换个号韩国红果果
JavaScriptcanvas
pixl的绘制,1.如果绘制点正处于相邻像素交叉线,绘制x像素的线宽,则从交叉线分别向前向后绘制x/2个像素,如果x/2是整数,则刚好填满x个像素,如果是小数,则先把整数格填满,再去绘制剩下的小数部分,绘制时,是将小数部分的颜色用来除以一个像素的宽度,颜色会变淡。所以要用整数坐标来画的话(即绘制点正处于相邻像素交叉线时),线宽必须是2的整数倍。否则会出现不饱满的像素。
2.如果绘制点为一个像素的
- 编码乱码问题
灵静志远
javajvmjsp编码
1、JVM中单个字符占用的字节长度跟编码方式有关,而默认编码方式又跟平台是一一对应的或说平台决定了默认字符编码方式;2、对于单个字符:ISO-8859-1单字节编码,GBK双字节编码,UTF-8三字节编码;因此中文平台(中文平台默认字符集编码GBK)下一个中文字符占2个字节,而英文平台(英文平台默认字符集编码Cp1252(类似于ISO-8859-1))。
3、getBytes()、getByte
- java 求几个月后的日期
darkranger
calendargetinstance
Date plandate = planDate.toDate();
SimpleDateFormat df = new SimpleDateFormat("yyyy-MM-dd");
Calendar cal = Calendar.getInstance();
cal.setTime(plandate);
// 取得三个月后时间
cal.add(Calendar.M
- 数据库设计的三大范式(通俗易懂)
aijuans
数据库复习
关系数据库中的关系必须满足一定的要求。满足不同程度要求的为不同范式。数据库的设计范式是数据库设计所需要满足的规范。只有理解数据库的设计范式,才能设计出高效率、优雅的数据库,否则可能会设计出错误的数据库.
目前,主要有六种范式:第一范式、第二范式、第三范式、BC范式、第四范式和第五范式。满足最低要求的叫第一范式,简称1NF。在第一范式基础上进一步满足一些要求的为第二范式,简称2NF。其余依此类推。
- 想学工作流怎么入手
atongyeye
jbpm
工作流在工作中变得越来越重要,很多朋友想学工作流却不知如何入手。 很多朋友习惯性的这看一点,那了解一点,既不系统,也容易半途而废。好比学武功,最好的办法是有一本武功秘籍。研究明白,则犹如打通任督二脉。
系统学习工作流,很重要的一本书《JBPM工作流开发指南》。
本人苦苦学习两个月,基本上可以解决大部分流程问题。整理一下学习思路,有兴趣的朋友可以参考下。
1 首先要
- Context和SQLiteOpenHelper创建数据库
百合不是茶
androidContext创建数据库
一直以为安卓数据库的创建就是使用SQLiteOpenHelper创建,但是最近在android的一本书上看到了Context也可以创建数据库,下面我们一起分析这两种方式创建数据库的方式和区别,重点在SQLiteOpenHelper
一:SQLiteOpenHelper创建数据库:
1,SQLi
- 浅谈group by和distinct
bijian1013
oracle数据库group bydistinct
group by和distinct只了去重意义一样,但是group by应用范围更广泛些,如分组汇总或者从聚合函数里筛选数据等。
譬如:统计每id数并且只显示数大于3
select id ,count(id) from ta
- vi opertion
征客丶
macoprationvi
进入 command mode (命令行模式)
按 esc 键
再按 shift + 冒号
注:以下命令中 带 $ 【在命令行模式下进行】,不带 $ 【在非命令行模式下进行】
一、文件操作
1.1、强制退出不保存
$ q!
1.2、保存
$ w
1.3、保存并退出
$ wq
1.4、刷新或重新加载已打开的文件
$ e
二、光标移动
2.1、跳到指定行
数字
- 【Spark十四】深入Spark RDD第三部分RDD基本API
bit1129
spark
对于K/V类型的RDD,如下操作是什么含义?
val rdd = sc.parallelize(List(("A",3),("C",6),("A",1),("B",5))
rdd.reduceByKey(_+_).collect
reduceByKey在这里的操作,是把
- java类加载机制
BlueSkator
java虚拟机
java类加载机制
1.java类加载器的树状结构
引导类加载器
^
|
扩展类加载器
^
|
系统类加载器
java使用代理模式来完成类加载,java的类加载器也有类似于继承的关系,引导类是最顶层的加载器,它是所有类的根加载器,它负责加载java核心库。当一个类加载器接到装载类到虚拟机的请求时,通常会代理给父类加载器,若已经是根加载器了,就自己完成加载。
虚拟机区分一个Cla
- 动态添加文本框
BreakingBad
文本框
<script> var num=1; function AddInput() { var str=""; str+="<input
- 读《研磨设计模式》-代码笔记-单例模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
public class Singleton {
}
/*
* 懒汉模式。注意,getInstance如果在多线程环境中调用,需要加上synchronized,否则存在线程不安全问题
*/
class LazySingleton
- iOS应用打包发布常见问题
chenhbc
iosiOS发布iOS上传iOS打包
这个月公司安排我一个人做iOS客户端开发,由于急着用,我先发布一个版本,由于第一次发布iOS应用,期间出了不少问题,记录于此。
1、使用Application Loader 发布时报错:Communication error.please use diagnostic mode to check connectivity.you need to have outbound acc
- 工作流复杂拓扑结构处理新思路
comsci
设计模式工作算法企业应用OO
我们走的设计路线和国外的产品不太一样,不一样在哪里呢? 国外的流程的设计思路是通过事先定义一整套规则(类似XPDL)来约束和控制流程图的复杂度(我对国外的产品了解不够多,仅仅是在有限的了解程度上面提出这样的看法),从而避免在流程引擎中处理这些复杂的图的问题,而我们却没有通过事先定义这样的复杂的规则来约束和降低用户自定义流程图的灵活性,这样一来,在引擎和流程流转控制这一个层面就会遇到很
- oracle 11g新特性Flashback data archive
daizj
oracle
1. 什么是flashback data archive
Flashback data archive是oracle 11g中引入的一个新特性。Flashback archive是一个新的数据库对象,用于存储一个或多表的历史数据。Flashback archive是一个逻辑对象,概念上类似于表空间。实际上flashback archive可以看作是存储一个或多个表的所有事务变化的逻辑空间。
- 多叉树:2-3-4树
dieslrae
树
平衡树多叉树,每个节点最多有4个子节点和3个数据项,2,3,4的含义是指一个节点可能含有的子节点的个数,效率比红黑树稍差.一般不允许出现重复关键字值.2-3-4树有以下特征:
1、有一个数据项的节点总是有2个子节点(称为2-节点)
2、有两个数据项的节点总是有3个子节点(称为3-节
- C语言学习七动态分配 malloc的使用
dcj3sjt126com
clanguagemalloc
/*
2013年3月15日15:16:24
malloc 就memory(内存) allocate(分配)的缩写
本程序没有实际含义,只是理解使用
*/
# include <stdio.h>
# include <malloc.h>
int main(void)
{
int i = 5; //分配了4个字节 静态分配
int * p
- Objective-C编码规范[译]
dcj3sjt126com
代码规范
原文链接 : The official raywenderlich.com Objective-C style guide
原文作者 : raywenderlich.com Team
译文出自 : raywenderlich.com Objective-C编码规范
译者 : Sam Lau
- 0.性能优化-目录
frank1234
性能优化
从今天开始笔者陆续发表一些性能测试相关的文章,主要是对自己前段时间学习的总结,由于水平有限,性能测试领域很深,本人理解的也比较浅,欢迎各位大咖批评指正。
主要内容包括:
一、性能测试指标
吞吐量、TPS、响应时间、负载、可扩展性、PV、思考时间
http://frank1234.iteye.com/blog/2180305
二、性能测试策略
生产环境相同 基准测试 预热等
htt
- Java父类取得子类传递的泛型参数Class类型
happyqing
java泛型父类子类Class
import java.lang.reflect.ParameterizedType;
import java.lang.reflect.Type;
import org.junit.Test;
abstract class BaseDao<T> {
public void getType() {
//Class<E> clazz =
- 跟我学SpringMVC目录汇总贴、PDF下载、源码下载
jinnianshilongnian
springMVC
----广告--------------------------------------------------------------
网站核心商详页开发
掌握Java技术,掌握并发/异步工具使用,熟悉spring、ibatis框架;
掌握数据库技术,表设计和索引优化,分库分表/读写分离;
了解缓存技术,熟练使用如Redis/Memcached等主流技术;
了解Ngin
- the HTTP rewrite module requires the PCRE library
流浪鱼
rewrite
./configure: error: the HTTP rewrite module requires the PCRE library.
模块依赖性Nginx需要依赖下面3个包
1. gzip 模块需要 zlib 库 ( 下载: http://www.zlib.net/ )
2. rewrite 模块需要 pcre 库 ( 下载: http://www.pcre.org/ )
3. s
- 第12章 Ajax(中)
onestopweb
Ajax
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- Optimize query with Query Stripping in Web Intelligence
blueoxygen
BO
http://wiki.sdn.sap.com/wiki/display/BOBJ/Optimize+query+with+Query+Stripping+in+Web+Intelligence
and a very straightfoward video
http://www.sdn.sap.com/irj/scn/events?rid=/library/uuid/40ec3a0c-936
- Java开发者写SQL时常犯的10个错误
tomcat_oracle
javasql
1、不用PreparedStatements 有意思的是,在JDBC出现了许多年后的今天,这个错误依然出现在博客、论坛和邮件列表中,即便要记住和理解它是一件很简单的事。开发者不使用PreparedStatements的原因可能有如下几个: 他们对PreparedStatements不了解 他们认为使用PreparedStatements太慢了 他们认为写Prepar
- 世纪互联与结盟有感
阿尔萨斯
10月10日,世纪互联与(Foxcon)签约成立合资公司,有感。
全球电子制造业巨头(全球500强企业)与世纪互联共同看好IDC、云计算等业务在中国的增长空间,双方迅速果断出手,在资本层面上达成合作,此举体现了全球电子制造业巨头对世纪互联IDC业务的欣赏与信任,另一方面反映出世纪互联目前良好的运营状况与广阔的发展前景。
众所周知,精于电子产品制造(世界第一),对于世纪互联而言,能够与结盟