杨辉三角c语言用矩阵,C语言中杨氏矩阵与杨辉三角的实现方法
一、杨氏矩阵
1.杨氏矩阵的概念
在数学中,杨表(英语:young tableau),又称杨氏矩阵。是对组合表示理论和舒伯特演算很有用的工具。它提供了一种方便的方式来描述对称和一般线性群的群表示,并研究它们的性质。杨表是剑桥大学数学家 alfred young 在1900年推提出。然后,它被弗罗贝尼乌斯应用对称群的研究中。他们的理论由许多数学家进一步发展,包括percymacmahon、w. v. d. hodge、g. de b. robinson、吉安-卡洛·罗塔、alain lascoux、marcel-paul schützenberger 和 richard p. stanley 等。
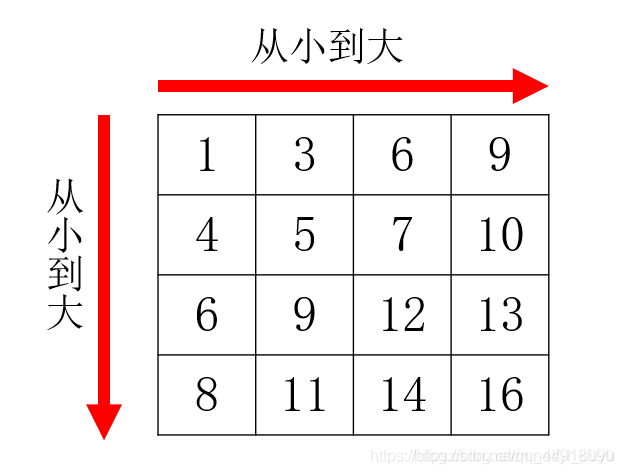
2.杨氏矩阵的图解
3.杨氏矩阵的实现
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
代码如下:
bool findnumberin2darray(int** matrix, int matrixsize, int* matrixcolsize, int target)
{
if(matrixsize==0||*matrixcolsize==0)
{
return false;
}
int row=0;
int col=*matrixcolsize-1;
while(row=0)
{
if(matrix[row][col]>target)
{
col--;
}
else if(matrix[row][col]
{
row++;
}
else if(matrix[row][col]==target)
{
return true;
}
}
return false;
}
二、杨辉三角
1.杨辉三角的概念
杨辉三角,是二项式系数在三角形中的一种几何排列。在欧洲,这个表叫做帕斯卡三角形。帕斯卡(1623----1662)是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年。杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合。
2.杨辉三角的图解
3.杨辉三角的实现
给定一个非负整数 numrows,生成杨辉三角的前 numrows 行。在杨辉三角中,每个数是它左上方和右上方的数的和。
代码如下:
#define _crt_secure_no_warnings 1
#include
int** generate(int numrows, int* returnsize, int** returncolumnsizes)
{
int row = 0;
int col = 0;
//ret是一个指针,它指向的是由指针构成的数组,指针指向对应的杨辉三角的一行数;ret也是二维数组
int** ret = (int**)malloc(sizeof(int*)*numrows);
//指定要返回的行数
*returnsize = numrows;
//分配每一列的具体空间
*returncolumnsizes = malloc(sizeof(int)*numrows);
for (row = 0; row < numrows; row++)
{
/* 分配杨辉三角中每一行的具体空间 */
ret[row] = malloc(sizeof(int)* (row + 1));
// 分配杨辉三角中每一行的列数
(*returncolumnsizes)[row] = row + 1;
ret[row][row] = ret[row][0] = 1;
for (col = 1; col < row; col++)
{
ret[row][col] = ret[row - 1][col - 1] + ret[row - 1][col];
}
}
return ret;
}
int main()
{
return 0;
}
总结
以上就是今天要讲的内容,本文仅仅简单介绍了数学中两个成就由来及代码实现,这类题目也很常见,我们务必掌握。
到此这篇关于c语言中杨氏矩阵与杨辉三角的实现方法的文章就介绍到这了,更多相关c语言杨氏矩阵与杨辉三角内容请搜索萬仟网以前的文章或继续浏览下面的相关文章希望大家以后多多支持萬仟网!