【算法与数据结构】101、LeetCode对称二叉树

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

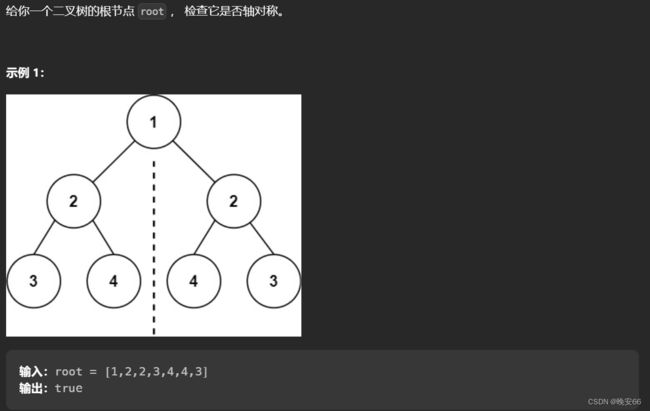
一、题目

二、递归法

  思路分析：这道题目标就是要对比左右两半的树是否对称，因此对比不是左右节点是否相等，而是根节点的左子树和右子树是否相等。刚开始笔者想到的是做层序遍历，然后判断每层的值是否前后对称，但是由于层序遍历当中空节点是不显示的，因此例二也会判成对称树。为此我们可以把空节点也显示出来，但是这样一来遍历的节点数量要大于等于树本身非空节点的数量，徒增计算量。经过一番思考，还是想用递归法实现。程序当中我们对比两个结点是否相等，一共有四种情况。其实还有一种情况，就是节点1的值等于节点2的值，这部分判断包含在cmpTree函数的递归语句return当中，如果出现第五种情况，最终会以第一种情况的形式返回。

• 1.节点1、节点2为空，对称，返回true；
• 2.节点1为空、节点2不为空， 不对称，返回false;
• 3.节点1不为空、节点2为空， 不对称，返回false;
• 4.节点1不为空、节点2不为空， 但值不相等，不对称，返回false;
    程序如下：

class Solution {
public:
    // 递归法
    bool cmpTree(TreeNode* node1, TreeNode* node2) {
        if (node1 == NULL && node2 == NULL) return true;    // 二者均为空节点
        if (node1 == NULL || node2 == NULL || node1->val != node2->val) return false;   // 其他三种情况
        return cmpTree(node1->left, node2->right) && cmpTree(node1->right, node2->left);
    }
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        return cmpTree(root->left, root->right);
    }
};

三、迭代法

  思路分析：迭代法使用了队列，先将根节点的左右节点压入队中，然后判断语句的思路和递归当中一致，最后再将要比较的节点按顺序入队，注意节点1的左节点和节点2的右节点比较，节点1的右节点和节点2的左节点比较。

class Solution2 {
public:
    // 迭代法
    bool isSymmetric(TreeNode* root) {
        if (!root) return true;     // 根节点为空，直接返回
        queue<TreeNode*> que;
        que.push(root->left);
        que.push(root->right);
        while (!que.empty()) {
            TreeNode* node1 = que.front(); 
            que.pop();
            TreeNode* node2 = que.front();
            que.pop();
            if (!node1 && !node2) continue;
            if (!node1 || !node2 || node1->val != node2->val) return false;
            que.push(node1->left);
            que.push(node2->right);
            que.push(node1->right);
            que.push(node2->left);
        }
        return true;
    }
};

三、完整代码

# include 
# include 
# include 
# include 
# include 
using namespace std;

// 树节点定义
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    // 递归法
    bool cmpTree(TreeNode* node1, TreeNode* node2) {
        if (node1 == NULL && node2 == NULL) return true;    // 二者均为空节点
        if (node1 == NULL || node2 == NULL || node1->val != node2->val) return false;   // 其他三种情况
        return cmpTree(node1->left, node2->right) && cmpTree(node1->right, node2->left);
    }
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        return cmpTree(root->left, root->right);
    }
};

class Solution2 {
public:
    // 迭代法
    bool isSymmetric(TreeNode* root) {
        if (!root) return true;     // 根节点为空，直接返回
        queue<TreeNode*> que;
        que.push(root->left);
        que.push(root->right);
        while (!que.empty()) {
            TreeNode* node1 = que.front(); 
            que.pop();
            TreeNode* node2 = que.front();
            que.pop();
            if (!node1 && !node2) continue;
            if (!node1 || !node2 || node1->val != node2->val) return false;
            que.push(node1->left);
            que.push(node2->right);
            que.push(node1->right);
            que.push(node2->left);
        }
        return true;
    }
};

void my_print2(vector<vector<int>>& v, string str) {
    cout << str << endl;
    for (vector<vector<int>>::iterator vit = v.begin(); vit < v.end(); ++vit) {
        for (vector<int>::iterator it = (*vit).begin(); it < (*vit).end(); ++it) {
            cout << *it << ' ';
        }
        cout << endl;
    }
}

// 前序遍历递归法创建二叉树，每次迭代将容器首元素弹出（弹出代码还可以再优化）
void Tree_Generator(vector<string>& t, TreeNode*& node) {
    if (t[0] == "NULL" || !t.size()) return;    // 退出条件
    else {
        node = new TreeNode(stoi(t[0].c_str()));    // 中
        t.assign(t.begin() + 1, t.end());
        Tree_Generator(t, node->left);              // 左
        t.assign(t.begin() + 1, t.end());
        Tree_Generator(t, node->right);             // 右
    }
}

vector<vector<int>> levelOrder(TreeNode* root) {
    queue<TreeNode*> que;
    if (root != NULL) que.push(root);
    vector<vector<int>> result;
    while (!que.empty()) {
        int size = que.size();  // size必须固定, que.size()是不断变化的
        vector<int> vec;
        for (int i = 0; i < size; ++i) {
            TreeNode* node = que.front();
            que.pop();
            vec.push_back(node->val);
            if (node->left) que.push(node->left);   // 空节点不入队
            if (node->right) que.push(node->right);
        }
        result.push_back(vec);
    }
    return result;
}

int main()
{
    vector<string> t = { "1", "2", "3", "NULL", "NULL", "4", "NULL", "NULL", "2", "4", "NULL", "NULL", "3", "NULL", "NULL" };   // 前序遍历
    //vector t = { "1", "2", "NULL", "3", "NULL", "NULL", "2", "NULL", "3", "NULL", "NULL" };   // 前序遍历
    TreeNode* root = new TreeNode();
    Tree_Generator(t, root);
    vector<vector<int>> tree = levelOrder(root);
    my_print2(tree, "目标树:");

    Solution2 s1;
    bool result = s1.isSymmetric(root);
    if (result) cout << "对称树" << endl;
    else cout << "非对称树" << endl;
    system("pause");
    return 0;
}

end