【深度学习】日常笔记14
对神经网络模型参数的初始化方案对保持数值稳定性有很重要的作用。初始化⽅案的选择可以与⾮线性激活函数的选择有趣的结合在⼀起。
突然有感触:做习题和模拟考研就分别是训练集和验证集,考研不就是最后的测试集()
p168的↓的解释:
(4.8.1)这个公式是表示深层网络的计算过程。在这个网络中,每一层的隐藏变量h(l)通过变换函数fl(h(l-1))得到,其中l表示层数,h(l-1)表示上一层的隐藏变量。最后的输出o是通过将所有层的变换函数依次作用在输入x上得到,即o = fL ◦ . . . ◦ f1(x),其中◦表示函数的复合(即依次执行函数的操作)。在深层网络中,我们有一系列的变换函数f(l),其中每个函数都作用在前一层的隐藏变量h(l-1)上,以产生当前层的隐藏变量h(l)。最后的输出o是通过将所有层的变换函数依次应用在输入x上得到。
在(4.8.2)公式中,"· . . . ·"的作用是表示多个项的乘积。具体来说,在(4.8.2)公式中的每个项都是对应的求偏导结果的乘积。公式右侧的每个项都对应着一个中间变量的偏导数与相应的中间变量的乘积。
例如,∂W(l)o = ∂h(L-1) h(L) · ∂h(l)h(l+1) · … · ∂W(l)h(l) 表示将所有∂h(L-1) h(L),∂h(l)h(l+1),∂W(l)h(l)这些项依次相乘。推导过程涉及到计算梯度(也就是导数)的链式法则。链式法则告诉我们如何计算复合函数的导数,根据(4.8.1)不难看出(4.8.2)的梯度推导是对的。
不稳定梯度带来的⻛险不⽌在于数值表⽰;不稳定梯度也威胁到我们优化算法的稳定性。我们可能⾯临⼀些问题。要么是梯度爆炸(gradient exploding)问题:参数更新过⼤,破坏了模型的稳定收敛;要么是梯度消失(gradient vanishing)问题:参数更新过⼩,在每次更新时⼏乎不会移动,导致模型⽆法学习。
梯度消失和梯度爆炸是深度⽹络中常⻅的问题。在参数初始化时需要⾮常⼩⼼,以确保梯度和参数可 以得到很好的控制。
解决梯度消失、梯度爆炸、参数化所固有的对称性的问题,可以在参数初始化上下功夫。
① 默认的随机初始化---正态分布初始化。
② Xavier初始化---Xavier初始化从均值为零,⽅差 σ2 = 2/(nin+nout) 的⾼斯分布中采样权重,nin 是当前层的输入度,nout 是当前层的输出维度,也可以将其改为选择从均匀分布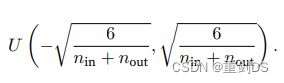 中抽取权重。Xavier初始化的理念是使得输入信号在前向传播过程中的方差和反向传播过程中的方差保持一致,以便更好地进行梯度传播。通过从高斯分布中采样权重,我们可以确保权重的初始化不会过于偏向较大或较小的值,避免了梯度消失或梯度爆炸的问题。因为在高斯分布中,大约 95% 的值会位于均值的两个标准差范围内,所以将方差设置为 2 / (nin + nout) 可以将大部分的权重值控制在合适的范围内。
中抽取权重。Xavier初始化的理念是使得输入信号在前向传播过程中的方差和反向传播过程中的方差保持一致,以便更好地进行梯度传播。通过从高斯分布中采样权重,我们可以确保权重的初始化不会过于偏向较大或较小的值,避免了梯度消失或梯度爆炸的问题。因为在高斯分布中,大约 95% 的值会位于均值的两个标准差范围内,所以将方差设置为 2 / (nin + nout) 可以将大部分的权重值控制在合适的范围内。
p172练习
1. 除了多层感知机的排列对称性之外,还能设计出其他神经⽹络可能会表现出对称性且需要被打破的情况吗?
答:
①对称激活函数:如果在神经网络的不同层中使用了相同的激活函数,且激活函数具有对称性,那么网络架构可能会表现出对称性。例如,如果所有层使用了相同的ReLU激活函数,它是一个对称的函数,可能导致梯度的方向不明确,使得网络训练困难。为了打破这种对称性,可以在每一层使用不同的激活函数,或者引入一些随机性,如dropout等。
②初始化权重的对称性:如果网络的初始权重具有某种对称性,比如在对称的权重矩阵中,不同的神经元连接具有相同的权重值。这种对称性可能导致网络在训练过程中收敛到相同或相似的权重配置。为了打破这种对称性,常用的方法是使用随机的权重初始化方式,如Glorot/Xavier初始化,以确保不同的神经元连接具有不同的初始权重值。
在这些情况下,为了使网络能够更好地学习和表示数据,需要打破对称性。这可以通过使用不同的激活函数、不同的初始化方法、引入随机性或正则化技术来实现。这样做可以增加网络的表达能力,提高网络的泛化能力,从而更好地适应数据和任务。
2. 我们是否可以将线性回归或softmax回归中的所有权重参数初始化为相同的值?
答:不推荐将线性回归或softmax回归中的所有权重参数初始化为相同的值。
当所有权重参数初始化为相同的值时,模型将没有足够的能力来学习特征之间重要性的差异。这可能导致模型的性能下降,以及对于复杂的数据集和模型,模型的学习能力受到限制。
4. 如果我们知道某些项是发散的,我们能在事后修正吗?看看关于按层⾃适应速率缩放的论⽂ (You et al., 2017) 。
答:
根据提供的参考文献(You et al., 2017),关于按层自适应速率缩放的论文,这是一种用于在训练过程中修正梯度发散问题的方法。
在深度学习中,梯度发散是指训练过程中梯度值变得非常大,导致权重更新过大,模型无法收敛或性能不稳定的问题。按层自适应速率缩放是一种方法,根据每个层的梯度值大小动态地调整学习率,以避免梯度发散问题。
该方法的关键思想是通过监测每个层的梯度变化情况,来决定是否对该层的梯度进行缩放。如果某个层的梯度值超过了一个预先设定的阈值,那么针对该层的学习率将被缩小,即减小权重更新的幅度。这样做可以防止梯度发散,并提高训练的稳定性和效果。
按层自适应速率缩放方法可以在训练过程中实时监控和调整各层的学习率,使其适应当前梯度的大小。通过对梯度发散的修正,该方法可以帮助模型更好地收敛,并提高性能。
总结而言,按层自适应速率缩放是一种可以在训练过程中修正梯度发散问题的方法。它通过动态调整每个层的学习率来避免梯度的发散,提高模型的训练稳定性和性能。
有时,根据测试集的精度衡量,模型表现得⾮常出⾊。但是当数据分布突然改变时,模型在部署中会出现灾难性的失败。更隐蔽的是,有时模型的部署本⾝就是扰乱数据分布的催化剂。举⼀个有点荒谬却可能真实存在的例⼦。假设我们训练了⼀个贷款申请⼈违约⻛险模型,⽤来预测谁将偿还贷款或违约。这个模型发现申请⼈的鞋⼦与违约⻛险相关(穿⽜津鞋申 请⼈会偿还,穿运动鞋申请⼈会违约)。此后,这个模型可能倾向于向所有穿着⽜津鞋的申请⼈发放贷款,并拒绝所有穿着运动鞋的申请⼈。这种情况可能会带来灾难性的后果。⾸先,⼀旦模型开始根据鞋类做出决定,顾客就会理解并改变他们的⾏为。不久,所有的申请者都会穿⽜津鞋,⽽信⽤度却没有相应的提⾼。幸运的是,在对未来我们的数据可能发⽣变化的⼀些限制性假设下,有些算法可以检测这种偏移,甚⾄可以 动态调整,提⾼原始分类器的精度。
由于协变量(特征)分布的变化⽽产⽣的问题,虽然输⼊的分布可能随时间⽽改变, 但标签函数(即条件分布P(y | x))没有改变,称为协变量偏移(covariate shift)。
考虑⼀下区分猫和狗的问题:训练数据包括 图4.9.1中的图像。
在测试时,我们被要求对 图4.9.2中的图像进⾏分类。
训练集由真实照⽚组成,⽽测试集只包含卡通图⽚。假设用于训练的训练集的特征与用于实际测试的测试集的特征关系不大,那如果没有⽅法来适应新的领域,可能会有⿇烦。
可以使用下面的协变量偏移纠正算法。假设我们有⼀个训练集{(x1, y1), . . . ,(xn, yn)},x加粗是因为表示特征向量,和⼀个未标记的测试集{u1, . . . , um}。对于协变量偏移,我们假设1 ≤ i ≤ n的xi来⾃某个源分布,ui来⾃⽬标分布。以下是纠正协变量偏移的典型算法:
1. 从概率密度为p的目标分布抽取的数据为1,从概率密度为q的源分布中抽取的数据为−1,生成⼀个⼆元分类训练集:{(x1, −1), . . . ,(xn, −1), (u1, 1), . . . ,(um, 1)}。
2. ⽤对数⼏率回归训练⼆元分类器得到函数h。
3. 使⽤βi = exp(h(xi))或更好的βi = min(exp(h(xi)), c)(c为常量)对训练数据进⾏加权。
4. 将权重βi扔进公式 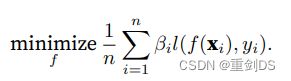 ,进行{(x1, y1), . . . ,(xn, yn)}的训练,从而得到真正需要的模型。
,进行{(x1, y1), . . . ,(xn, yn)}的训练,从而得到真正需要的模型。
当我们认为y导致x时,这⾥我们假设标签边缘概率P(y)可以改变,但是类别条件分布P(x | y)在不同的领域之间保持不变,就称为标签偏移(label shift)。例如:预测患者的疾病,我们可能根据症状来判断,即使疾病的相对流⾏率随着时间的推移⽽变化。标签偏移在这 ⾥是恰当的假设,因为疾病会引起症状。



