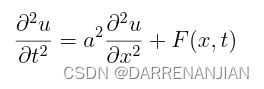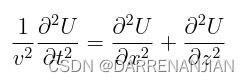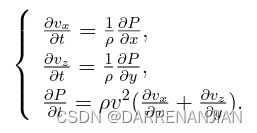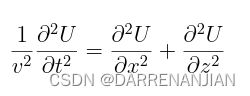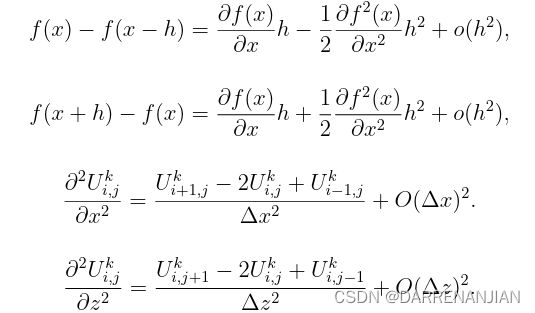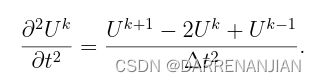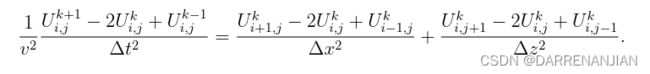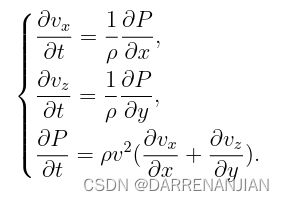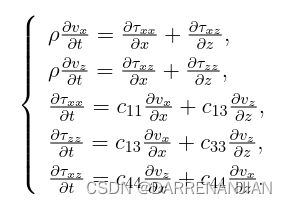地震正演培训
目录
一. day_1
1. 正演的目的
2. 介绍几种的方程
2.1 弦振动方程
2.2 二维声波方程
2.3 二维弹性波方程
二. day_2
1. 网格剖分
2. 泰勒展开
3. 程序理解
3.1 代码如下所示
3.2 结果展示
三. day_3
1. 边界情况
2. 波场快照
3. 合成的数据记录
4. 作业展示
5. 代码(包含边界)
四. day_4
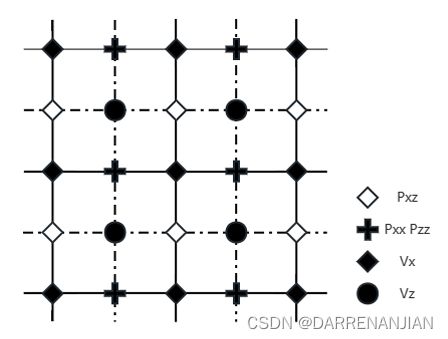
1. 交错网格
2. 作业
五. day_5
1. 交错网格
2. 作业
六. 总结
一. day_1
1. 正演的目的
正演模拟,是在地球物理勘探研究中,根据地质体的形状、产状和物性数据,通过构造数学模型计算得到其理论值(数学模拟),或通过构造实体模型来观测模型所产生的地球物理效应的数值(物理模拟)。
在地球物理资料解释过程中,常常利用正演模拟结果与实际地球物理勘探资料进行比较,不断修正模型,使模拟结果与实际资料尽可能地接近,进而使解释结果更接近客观实际。
总结就是一句:根据我们认为建立的速度模型(当然是尽可能符合地层的情况),然后求解出地震波在这个地层的传播情况,也可以理解为解方程。整个过程不涉及机器学习的概念,但是求解得到的地震波数据可以被反过来应用于地震的反演,用于验证反演的模拟情况。
2. 介绍几种的方程
2.1 弦振动方程
2.2 二维声波方程
对应的一阶速度-应力格式
2.3 二维弹性波方程
二. day_2
要求解如下的方程
1. 网格剖分
2. 泰勒展开
通过泰勒展开可以将U对于空间维度上面的倒数离散化,从而求解,详细过程如下所示:
同理,将U对于时间层面的倒数也通过泰勒展开求解
组合起来
3. 程序理解
3.1 代码如下所示
这里关键是理解震源的波动情况,并且通过上一时间层面的参数来更新下一层面的参数,不断迭代,从而得到最终时间的传播情况。
% 声波二维均匀模型-中心差分格式
tic
clc
close all
clear all
Endtime=0.5; %模拟时长
delta_t=0.0005;%以秒为单位
delta_x=6;%以米为单位 空间步长
delta_z=6;
CNX=301; %x方向的网格数
CNZ=301; %
v=1500; %波速
Sx=(CNX+1)/2; %震源位置
Sz=(CNZ+1)/2;
f0=30;% 10~40HZ 震源主频
Unow=zeros(CNX,CNZ);
Uprev=zeros(CNX,CNZ);
Unext=zeros(CNX,CNZ);
% 主程序
for time=0:delta_t:Endtime
for i=2:CNX-1
for j=2:CNZ-1
A=(-2*Unow(i,j)+Unow(i+1,j)+Unow(i-1,j))/delta_x^2;
B=(-2*Unow(i,j)+Unow(i,j+1)+Unow(i,j-1))/delta_z^2;
Unext(i,j)=2*Unow(i,j)-Uprev(i,j)+v^2*(A+B)*delta_t^2;
end
end
Unext(Sx,Sz)=5.76*f0^2*(1-16*(0.6*f0*time-1)^2)*exp(-8*(0.6*f0*time-1)^2);%震源函数
Uprev=Unow; %波场更新
Unow=Unext;
end
%绘图
surf(Unow)
shading interp;
view(2);%view(90,90)
colormap(gray);
toc3.2 结果展示
对应时间为0.3秒波传播的结果
对应时间为0.5秒波传播的结果
三. day_3
1. 边界情况
当波传递到边界的一种情况,这里我们设置反射系数的绝对值为1,
这里我们设置吸收边界条件
2. 波场快照
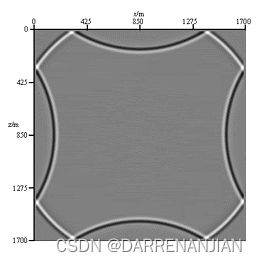
均匀模型
层状模型
有不同的底层,从而产生反射
 标题
标题
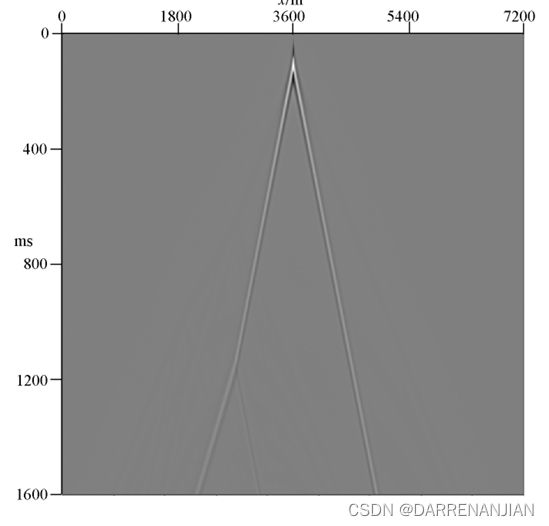
3. 合成的数据记录
这里即将图1的数据(三维数据)换了一个角度记录的数据
4. 作业展示
将如下代码转化为对应的泰勒展开形式
A=(-2.8194*Unow(m,n)+1.575*(Unow(m+1,n)+Unow(m-1,n))-0.1827*(Unow(m+2,n)+Unow(m-2,n))+0.0174*(Unow(m+3,n)+Unow(m-3,n)))/delta_x^2;
B=(-2.8194*Unow(m,n)+1.575*(Unow(m,n+1)+Unow(m,n-1))-0.1827*(Unow(m,n+2)+Unow(m,n-2))+0.0174*(Unow(m,n+3)+Unow(m,n-3)))/delta_z^2;
Unext(m,n)=2*Unow(m,n)-Uprev(m,n)+c^2*(A+B)*delta_t^2;5. 代码(包含边界)
% 声波二阶-添加边界-常规网格
tic
clc
close all
clear all
Endtime=0.4; %模拟时长
delta_t=0.001;%以秒为单位
delta_x=0.006;%以千米为单位 空间步长
delta_z=0.006;
f0=30;% 10~40HZ 震源频率
iteration=1;
nk=1;
n=Endtime/delta_t;
CNX=301; %
CNZ=301; %
BNX=20;
BNZ=20;
XMAX=CNX+2*BNX;
ZMAX=CNZ+2*BNZ;
Sx=(XMAX+1)/2; %震源位置
Sz=(ZMAX+1)/2;
c=0;
%zeros(XMAX,ZMAX);%波速
v(1:100,1:ZMAX)=2.0;
v(101:200,1:ZMAX)=2.0;
v(201:XMAX,1:ZMAX)=2;
a=-0.15;
S=0.001;
Wave=zeros(n+1,1);
Fnow=zeros(n+1,CNZ);
Unow=zeros(XMAX,ZMAX);
Uprev=zeros(XMAX,ZMAX);
Unext=zeros(XMAX,ZMAX);
Uxnow=zeros(XMAX,ZMAX);%n
Uxprev=zeros(XMAX,ZMAX);%n-1
Uxnext=zeros(XMAX,ZMAX);%n+1
Uznow=zeros(XMAX,ZMAX);%n
Uzprev=zeros(XMAX,ZMAX);%n-1
Uznext=zeros(XMAX,ZMAX);%n+1
Psi2x=zeros(2*BNZ,XMAX);
Uxxprev=zeros(2*BNZ,XMAX);
Psi2xprev=zeros(2*BNZ,XMAX);
Eta2xprev=zeros(2*BNZ,XMAX);
Eta2x=zeros(2*BNZ,XMAX);
Psixprev=zeros(2*BNZ,XMAX);
Psix=zeros(2*BNZ,XMAX);
Etaxprev=zeros(2*BNZ,XMAX);
Etax=zeros(2*BNZ,XMAX);
Thetaxprev=zeros(2*BNZ,XMAX);
Thetax=zeros(2*BNZ,XMAX);
Uzzprev=zeros(ZMAX,2*BNZ);
Psi2zprev=zeros(ZMAX,2*BNZ);
Psi2z=zeros(ZMAX,2*BNZ);
Eta2zprev=zeros(ZMAX,2*BNZ);
Eta2z=zeros(ZMAX,2*BNZ);
Psizprev=zeros(ZMAX,2*BNZ);
Psiz=zeros(ZMAX,2*BNZ);
Etazprev=zeros(ZMAX,2*BNZ);
Etaz=zeros(ZMAX,2*BNZ);
Thetazprev=zeros(ZMAX,2*BNZ);
Thetaz=zeros(ZMAX,2*BNZ);
% 主程序
for time=0:delta_t:Endtime
for m=4:XMAX-3
for n=4:ZMAX-3
c=v(m,n);
%A=(-2*Unow(m,n)+Unow(m+1,n)+Unow(m-1,n))/delta_x^2;
%B=(-2*Unow(m,n)+Unow(m,n+1)+Unow(m,n-1))/delta_z^2;
A=(-2.8194*Unow(m,n)+1.575*(Unow(m+1,n)+Unow(m-1,n))-0.1827*(Unow(m+2,n)+Unow(m-2,n))+0.0174*(Unow(m+3,n)+Unow(m-3,n)))/delta_x^2;
B=(-2.8194*Unow(m,n)+1.575*(Unow(m,n+1)+Unow(m,n-1))-0.1827*(Unow(m,n+2)+Unow(m,n-2))+0.0174*(Unow(m,n+3)+Unow(m,n-3)))/delta_z^2;
Unext(m,n)=2*Unow(m,n)-Uprev(m,n)+c^2*(A+B)*delta_t^2;
%fprintf('their is %8.5f\n',c);
%***************添加边界***************
if m<=BNX+1 || m>=BNX+CNX || n<=BNZ+1 || n>=BNZ+CNZ
Uxx=A;
Uzz=B;
%U的X方向****************************
if m<=BNX+1 || m>=CNX+BNX
if m<=BNX+1
XBPos=m;
XBDistance=(BNX+1-m)*delta_x;
else
XBPos=m-CNX;
XBDistance=(m-(BNX+CNX))*delta_x;
end
ZBPos=n;
XBThick=BNX*delta_x ;
XDecay=-3*c*log(S)/(2*XBThick)*(XBDistance/XBThick)^2;
XDecay_order=-3*c*log(S)*XBDistance/XBThick^3;
XAlpha=pi*f0*(1-XBDistance/XBThick);
XAlpha_order=-pi*f0/XBThick;
bX=exp(-(XDecay+XAlpha)*delta_t);
aX=(1-bX)/(XDecay+XAlpha);
%傅里叶逆变换各部分表达式
Psi2x(XBPos,ZBPos)=bX*Psi2xprev(XBPos,ZBPos)+aX*0.5*(Uxx+Uxxprev(XBPos,ZBPos));
Eta2x(XBPos,ZBPos)=bX*Eta2xprev(XBPos,ZBPos)+aX*0.5*(Psi2x(XBPos,ZBPos)+Psi2xprev(XBPos,ZBPos));
Psix(XBPos,ZBPos)=bX*Psixprev(XBPos,ZBPos)+aX*0.5*(Uxnow(m,n)+Uxprev(m,n));
Etax(XBPos,ZBPos)=bX*Etaxprev(XBPos,ZBPos)+aX*0.5*(Psix(XBPos,ZBPos)+Psixprev(XBPos,ZBPos)) ;
Thetax(XBPos,ZBPos)=bX*Thetaxprev(XBPos,ZBPos)+aX*0.5*(Etax(XBPos,ZBPos)+Etaxprev(XBPos,ZBPos)) ;
%指标变换——迭代更新
Uxxprev(XBPos,ZBPos)=Uxx;
Psi2xprev(XBPos,ZBPos)=Psi2x(XBPos,ZBPos);
Eta2xprev(XBPos,ZBPos)=Eta2x(XBPos,ZBPos);
Psixprev(XBPos,ZBPos)=Psix(XBPos,ZBPos);
Etaxprev(XBPos,ZBPos)=Etax(XBPos,ZBPos);
Thetaxprev(XBPos,ZBPos)=Thetax(XBPos,ZBPos);
%U的X方向二阶偏导数的傅里叶逆变换表达式
Uxx=Uxx-2*XDecay*Psi2x(XBPos,ZBPos)+XDecay^2*Eta2x(XBPos,ZBPos)-XDecay_order*Psix(XBPos,ZBPos)...
+XDecay*(2*XDecay_order+XAlpha_order)*Etax(XBPos,ZBPos)-XDecay^2*(XDecay_order+XAlpha_order)*Thetax(XBPos,ZBPos);
end
% **************U的Z方向****************************
if n<=BNZ+1 || n>=BNZ+CNZ
if n<=BNZ+1
ZBPos=n;
ZBDistance=(BNZ+1-n)*delta_z;
else
ZBPos=n-CNZ;
ZBDistance=(n-(BNZ+CNZ))*delta_z;
end
XBPos=m;
ZBThick=BNZ*delta_z;
ZDecay=-3*c/(2*ZBThick)*log(S)*(ZBDistance/ZBThick)^2;
ZDecay_order=-3*c*log(S)*ZBDistance/ZBThick^3;
ZAlpha=pi*f0*(1-ZBDistance/ZBThick);
ZAlpha_order=-pi*f0/ZBThick;
bZ=exp(-(ZDecay+ZAlpha)*delta_t);
aZ=(1-bZ)/(ZDecay+ZAlpha);
%傅里叶逆变换各部分表达式
Psi2z(XBPos,ZBPos)=bZ*Psi2zprev(XBPos,ZBPos)+aZ*0.5*(Uzz+Uzzprev(XBPos,ZBPos));
Eta2z(XBPos,ZBPos)=bZ*Eta2zprev(XBPos,ZBPos)+aZ*0.5*(Psi2z(XBPos,ZBPos)+Psi2zprev(XBPos,ZBPos));
Psiz(XBPos,ZBPos)=bZ*Psizprev(XBPos,ZBPos)+aZ*0.5*(Uznow(m,n)+Uzprev(m,n));
Etaz(XBPos,ZBPos)=bZ*Etazprev(XBPos,ZBPos)+aZ*0.5*(Psiz(XBPos,ZBPos)+Psizprev(XBPos,ZBPos)) ;
Thetaz(XBPos,ZBPos)=bZ*Thetazprev(XBPos,ZBPos)+aZ*0.5*(Etaz(XBPos,ZBPos)+Etazprev(XBPos,ZBPos)) ;
%指标变换——迭代更新
Uzzprev(XBPos,ZBPos)=Uzz;
Psi2zprev(XBPos,ZBPos)=Psi2z(XBPos,ZBPos);
Eta2zprev(XBPos,ZBPos)=Eta2z(XBPos,ZBPos);
Psizprev(XBPos,ZBPos)=Psiz(XBPos,ZBPos);
Etazprev(XBPos,ZBPos)=Etaz(XBPos,ZBPos);
Thetazprev(XBPos,ZBPos)=Thetaz(XBPos,ZBPos);
%Z方向二阶偏导数的傅里叶逆变换表达式
Uzz=Uzz-2*ZDecay*Psi2z(XBPos,ZBPos)+ZDecay^2*Eta2z(XBPos,ZBPos)-ZDecay_order*Psiz(XBPos,ZBPos)...
+ZDecay*(2*ZDecay_order+ZAlpha_order)*Etaz(XBPos,ZBPos)-ZDecay^2*(ZDecay_order+ZAlpha_order)*Thetaz(XBPos,ZBPos);
end
Unext(m,n)=2*Unow(m,n)-Uprev(m,n)+(c*delta_t)^2*(Uxx+Uzz);
end %边界循环结束
if m == Sx
Fnow(nk,n) = Unext(Sx,n);%地震记录
end
Wave(iteration) = Unext(101,151); %波形图
iteration = iteration + 1;
end
end
Unext(Sx,Sz)=delta_t^2*5.76*f0^2*(1-16*(0.6*f0*time-1)^2)*exp(-8*(0.6*f0*time-1)^2);
Uprev=Unow; %波场更新
Unow=Unext;
nk=nk+1;
end
%绘图
%plot(Wave)
%surf(Unow)
surf(Fnow)
shading interp;
view(2);%view(90,90)
colormap(gray);
toc四. day_4
需要求解的方程
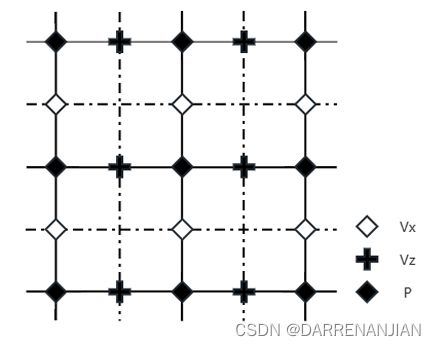
1. 交错网格
在之前的网格剖分上将网格细化,但是这并没有增加多少计算量(提高计算精度,但是时间复杂度仅仅增加了常数级)。今天的任务主要是理解交错网格剖分
这里还有公式的推导我就不详细赘述,详情参考class4.pdf
2. 作业
五. day_5
需要求解的方程
1. 交错网格
换汤不换药,原理不变,只是改变了方程而已。
2. 作业
六. 总结
正演培训结束之后,我认为最重要的部分是对于偏导的泰勒展开,这是求解方程的基础,这里的公式推导明白之后,后面的都是在这基础之上增加(交错网格)。但是最本质的原理还是差分法求解方程。
除此之外,能够更进一步理解地震数据——速度模型,地震波数据。