【统计学习方法】第7章 支持向量机

支持向量机（support vector machines，SVM）是一种二类分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；支持向量机还包括核技巧，这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化，可形式化为一个求解凸二次规划（convex quadratic programming）的问题，也等价于正则化的合页损失函数的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化算法。

1、线性可分支持向量机与硬间隔最大化

线性可分支持向量机

假设给定一个特征空间上的训练数据集$$\begin{array}{rl}& T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}\end{array}$$

其中，$x_i\in \mathcal{X}=R^n,y_i\in \mathcal{Y}=\left\{+1,-1\right\},i=1,2,\cdots ,N$，$x_i$为第$i$个特征向量（实例），$y_i$为第$x_i$的类标记，当$y_i=+1$时，称$x_i$为正例；当$y_i=-1$时，称$x_i$为负例，$\left(x_i,y_i\right)$称为样本点。

分离超平面对应于方程$w.x+b=0$，它由法向量$w$和截距$b$决定，可用$(w,b)$来表示。

线性可分支持向量机（硬间隔支持向量机）：给定线性可分训练数据集，通过间隔最大化或等价地求解相应地凸二次规划问题学习得到分离超平面为$$\begin{array}{rl}& w^{\ast }\cdot x+b^{\ast }=0\end{array}$$

以及相应的分类决策函数$$\begin{array}{rl}& f\left(x\right)=sign\left(w^{\ast }\cdot x+b^{\ast }\right)\end{array}$$

称为线型可分支持向量机。

函数间隔和几何间隔

对于给定的训练数据集T和超平面$(w,b)$，定义超平面$\left(w,b\right)$关于样本点$\left(x_i,y_i\right)$的函数间隔为$$\begin{array}{rl}& {\hat{\gamma }}_i=y_i\left(w\cdot x_i+b\right)\end{array}$$

超平面$\left(w,b\right)$关于训练集$T$的函数间隔$$\begin{array}{rl}& \hat{\gamma }=\underset{i=1,2,\cdots ,N}{\min }{\hat{\gamma }}_i\end{array}$$

即超平面$\left(w,b\right)$关于训练集$T$中所有样本点$\left(x_i,y_i\right)$的函数间隔的最小值。

超平面$\left(w,b\right)$关于样本点$\left(x_i,y_i\right)$的几何间隔为$$\begin{array}{rl}& {\gamma }_i=y_i\left(\frac{w}{\Vert w\Vert }\cdot x_i+\frac{b}{\Vert w\Vert }\right)\end{array}$$

超平面$\left(w,b\right)$关于训练集$T$的几何间隔$$\begin{array}{rl}& \gamma =\underset{i=1,2,\cdots ,N}{\min }{\gamma }_i\end{array}$$

即超平面$\left(w,b\right)$关于训练集$T$中所有样本点$\left(x_i,y_i\right)$的几何间隔的最小值。

函数间隔和几何间隔的关系$$\begin{array}{rl}& {\gamma }_i=\frac{{\hat{\gamma }}_i}{\Vert w\Vert }\\ & \gamma =\frac{\hat{\gamma }}{\Vert w\Vert }\end{array}$$

间隔最大化

最大间隔分离超平面等价为求解$$\begin{array}{rl}& \underset{w,b}{\max }\gamma \\ & s.t.y_i\left(\frac{w}{\Vert w\Vert }\cdot x_i+\frac{b}{\Vert w\Vert }\right)\ge \gamma ,i=1,2,\cdots ,N\end{array}$$

等价的$$\begin{array}{rl}& \underset{w,b}{\max }\frac{\hat{\gamma }}{\Vert w\Vert }\\ & s.t.y_i\left(w\cdot x_i+b\right)\ge \hat{\gamma },i=1,2,\cdots ,N\end{array}$$

取$\hat{\gamma }=1$，将其入上面的最优化问题，注意到最大化$\frac{1}{\Vert w\Vert }$和最小化$\frac{1}{2}\Vert w{\Vert }^2$是等价的，

等价的$$\begin{array}{rl}& \underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2\\ & s.t.y_i\left(w\cdot x_i+b\right)-1\ge 0,i=1,2,\cdots ,N\end{array}$$

线性可分支持向量机学习算法（最大间隔法）：

• 输入：线性可分训练数据集$T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$，其中$x_i\in \mathcal{X}=R^n,y_i\in \mathcal{Y}=\left\{+1,-1\right\},i=1,2,\cdots ,N$
• 输出：最大间隔分离超平面和分类决策函数

1. 构建并求解约束最优化问题$$\begin{array}{rl}& \\ & \underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2\\ & s.t.y_i\left(w\cdot x_i+b\right)-1\ge 0,i=1,2,\cdots ,N\end{array}$$
   求得最优解$w^{\ast },b^{\ast }$。
2. 得到分离超平面$$\begin{array}{rl}& w^{\ast }\cdot x+b^{\ast }=0\end{array}$$

以及分类决策函数
$$\begin{array}{rl}& f\left(x\right)=sign\left(w^{\ast }\cdot x+b^{\ast }\right)\end{array}$$

支持向量和间隔边界

（硬间隔）支持向量：训练数据集的样本点中与分离超平面距离最近的样本点的实例，即使约束条件等号成立的样本点$$\begin{array}{rl}& y_i\left(w\cdot x_i+b\right)-1=0\end{array}$$

对$y_i=+1$的正例点，支持向量在超平面
$$\begin{array}{rl}& H_1:w\cdot x+b=1\end{array}$$

对$y_i=-1$的正例点，支持向量在超平面
$$\begin{array}{rl}& H_1:w\cdot x+b=-1\end{array}$$

$H_1$和$H_2$称为间隔边界，$H_1$和$H_2$上的点就是支持向量。

$H_1$和$H_2$之间的距离称为间隔，且$|H_1{H}_2|=\frac{1}{\Vert w\Vert }+\frac{1}{\Vert w\Vert }=\frac{2}{\Vert w\Vert }$。

2、线性支持向量机与软间隔最大化

线性支持向量机

线性支持向量机（软间隔支持向量机）：给定线性不可分训练数据集，通过求解凸二次规划问题
$$\begin{array}{rl}& \underset{w,b,\xi }{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N{\xi }_i\\ & s.t.y_i\left(w\cdot x_i+b\right)\ge 1-{\xi }_i\\ & {\xi }_i\ge 0,i=1,2,\cdots ,N\end{array}$$

学习得到分离超平面为$$\begin{array}{rl}& w^{\ast }\cdot x+b^{\ast }=0\end{array}$$

以及相应的分类决策函数$$\begin{array}{rl}& f\left(x\right)=sign\left(w^{\ast }\cdot x+b^{\ast }\right)\end{array}$$

称为线型支持向量机。

最优化问题的求解：

1. 引入拉格朗日乘子${\alpha }_i\ge 0,i=1,2,\cdots ,N$构建拉格朗日函数$$\begin{array}{rl}& L\left(w,b,\alpha \right)=\frac{1}{2}\Vert w{\Vert }^2+\sum _{i=1}^N{\alpha }_i\left[-y_i\left(w\cdot x_i+b\right)+1\right]\\ & =\frac{1}{2}\Vert w{\Vert }^2-\sum _{i=1}^N{\alpha }_i{y}_i\left(w\cdot x_i+b\right)+\sum _{i=1}^N{\alpha }_i\end{array}$$
   其中，$\alpha ={\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_N\right)}^T$为拉格朗日乘子向量。

2. 求${\min }_{w,b}L\left(w,b,\alpha \right)$:$$\begin{array}{rl}& {\nabla }_{w}L\left(w,b,\alpha \right)=w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0\\ & {\nabla }_{b}L\left(w,b,\alpha \right)=-\sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$

   得
   $$\begin{array}{rl}& w＝\sum _{i=1}^N{\alpha }_i{y}_i{x}_i\\ & \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$

   代入拉格朗日函数，得$$\begin{array}{rl}& \\ & L\left(w,b,\alpha \right)=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i{y}_i\left[\left(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\right)\cdot x_i+b\right]+\sum _{i=1}^N{\alpha }_i\\ & =-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i{y}_{i}b+\sum _{i=1}^N{\alpha }_i\\ & =-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)+\sum _{i=1}^N{\alpha }_i\end{array}$$
   即$$\begin{array}{rl}& \\ & \underset{w,b}{\min }L\left(w,b,\alpha \right)=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)+\sum _{i=1}^N{\alpha }_i\end{array}$$

3. 求${\max }_{\alpha }{\min }_{w,b}L\left(w,b,\alpha \right)$:$$\begin{array}{rl}& \\ & \underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)+\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i\ge 0,i=1,2,\cdots ,N\end{array}$$
   等价的$$\begin{array}{rl}& \\ & \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i\ge 0,i=1,2,\cdots ,N\end{array}$$

线性可分支持向量机（硬间隔支持向量机）学习算法：

• 输入：线性可分训练数据集$T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$，其中$x_i\in \mathcal{X}=R^n,y_i\in \mathcal{Y}=\left\{+1,-1\right\},i=1,2,\cdots ,N$
• 输出：最大间隔分离超平面和分类决策函数

1. 构建并求解约束最优化问题$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i\ge 0,i=1,2,\cdots ,N\end{array}$$

   求得最优解$${\alpha }^{\ast }=\left({\alpha }_1^{\ast },{\alpha }_1^{\ast },\cdots ,{\alpha }_N^{\ast }\right)$$

2. 计算$$\begin{array}{rl}& w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\end{array}$$

   并选择${\alpha }^{\ast }$的一个正分量${\alpha }_j^{\ast }>0$，计算$$\begin{array}{rl}& b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\left(x_i\cdot x_j\right)\end{array}$$

3. 得到分离超平面$$\begin{array}{rl}& w^{\ast }\cdot x+b^{\ast }=0\end{array}$$

   以及分类决策函数
   $$\begin{array}{rl}& f\left(x\right)=sign\left(w^{\ast }\cdot x+b^{\ast }\right)\end{array}$$

最优化问题的求解：

1. 引入拉格朗日乘子${\alpha }_i\ge 0,{\mu }_i\ge 0,i=1,2,\cdots ,N$构建拉格朗日函数$$\begin{array}{rl}& L\left(w,b,\xi ,\alpha ,\mu \right)=\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N{\xi }_i+\sum _{i=1}^N{\alpha }_i\left[-y_i\left(w\cdot x_i+b\right)+1-{\xi }_i\right]+\sum _{i=1}^N{\mu }_i\left(-{\xi }_i\right)\\ & =\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i\left[y_i\left(w\cdot x_i+b\right)-1+{\xi }_i\right]-\sum _{i=1}^N{\mu }_i{\xi }_i\end{array}$$

   其中，$\alpha ={\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_N\right)}^T$以及$\mu ={\left({\mu }_1,{\mu }_2,\cdots ,{\mu }_N\right)}^T$为拉格朗日乘子向量。

2. 求${\min }_{w,b}L\left(w,b,\xi ,\alpha ,\mu \right)$:$$\begin{array}{rl}& {\nabla }_{w}L\left(w,b,\xi ,\alpha ,\mu \right)=w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0\\ & {\nabla }_{b}L\left(w,b,\xi ,\alpha ,\mu \right)=-\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\nabla }_{{\xi }_i}L\left(w,b,\xi ,\alpha ,\mu \right)=C-{\alpha }_i-{\mu }_i=0\end{array}$$

   得
   $$\begin{array}{rl}& w＝\sum _{i=1}^N{\alpha }_i{y}_i{x}_i\\ & \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & C-{\alpha }_i-{\mu }_i=0\end{array}$$

   代入拉格朗日函数，得$$\begin{array}{rl}& L\left(w,b,\xi ,\alpha ,\mu \right)=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i{y}_i\left[\left(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\right)\cdot x_i+b\right]\\ & +\sum _{i=1}^N{\alpha }_i-\sum _{i=1}^N{\alpha }_i{\xi }_i-\sum _i^N{\mu }_i{\xi }_i\\ & =-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i{y}_{i}b+\sum _{i=1}^N{\alpha }_i+\sum _{i=1}^N{\xi }_i\left(C-{\alpha }_i-{\mu }_i\right)\\ & =-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)+\sum _{i=1}^N{\alpha }_i\end{array}$$

   即$$\begin{array}{rl}& \underset{w,b,\xi }{\min }L\left(w,b,\xi ,\alpha ,\mu \right)=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)+\sum _{i=1}^N{\alpha }_i\end{array}$$

3. 求${\max }_{\alpha }{\min }_{w,b,\xi }L\left(w,b,\xi ,\alpha ,\mu \right)$:$$\begin{array}{rl}& \underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)+\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & C-{\alpha }_i-{\mu }_i=0\\ & {\alpha }_i\ge 0\\ & {\mu }_i\ge 0,i=1,2,\cdots ,N\end{array}$$

等价的$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,\cdots ,N\end{array}$$

线性支持向量机（软间隔支持向量机）学习算法：

• 输入：训练数据集$T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$，其中$x_i\in \mathcal{X}=R^n,y_i\in \mathcal{Y}=\left\{+1,-1\right\},i=1,2,\cdots ,N$
• 输出：最大间隔分离超平面和分类决策函数

1. 选择惩罚参数$C\ge 0$，构建并求解约束最优化问题$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,\cdots ,N\end{array}$$

   求得最优解$${\alpha }^{\ast }=\left({\alpha }_1^{\ast },{\alpha }_1^{\ast },\cdots ,{\alpha }_N^{\ast }\right)$$

2. 计算$$\begin{array}{rl}& w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\end{array}$$

   并选择${\alpha }^{\ast }$的一个分量$0<{\alpha }_j^{\ast }<C$，计算$$\begin{array}{rl}& b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\left(x_i\cdot x_j\right)\end{array}$$

3. 得到分离超平面$$\begin{array}{rl}& w^{\ast }\cdot x+b^{\ast }=0\end{array}$$

   以及分类决策函数
   $$\begin{array}{rl}& f\left(x\right)=sign\left(w^{\ast }\cdot x+b^{\ast }\right)\end{array}$$

支持向量

（软间隔）支持向量：线性不可分情况下，最优化问题的解$${\alpha }^{\ast }={\left({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }\right)}^T$$中对应于${\alpha }_i^{\ast }>0$的样本点$\left(x_i,y_i\right)$的实例$x_i$。

实例$x_i$的几何间隔$$\begin{array}{rl}& {\gamma }_i=\frac{y_i\left(w\cdot x_i+b\right)}{\Vert w\Vert }=\frac{|1-{\xi }_i|}{\Vert w\Vert }\end{array}$$

且$\frac{1}{2}|H_1{H}_2|=\frac{1}{\Vert w\Vert }$

则实例$x_i$到间隔边界的距离$$\begin{array}{rl}& \left|{\gamma }_i-\frac{1}{\Vert w\Vert }\right|=\left|\frac{|1-{\xi }_i|}{\Vert w\Vert }-\frac{1}{\Vert w\Vert }\right|=\frac{{\xi }_i}{\Vert w\Vert }\end{array}$$

$$\begin{array}{r}{\xi }_i\ge 0\iff \{\begin{array}{rl}& {\xi }_i=0,x_i在间隔边界上;\\ & 0<{\xi }_i<1,x_i在间隔边界与分离超平面之间;\\ & {\xi }_i=1,x_i在分离超平面上;\\ & {\xi }_i>1,x_i在分离超平面误分类一侧;\end{array}\end{array}$$

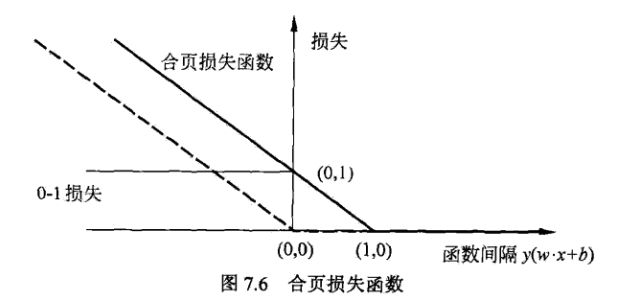
合页损失函数

线性支持向量机（软间隔）的合页损失函数$$\begin{array}{rl}& L\left(y\left(w\cdot x+b\right)\right)={\left[1-y\left(w\cdot x+b\right)\right]}_{+}\end{array}$$

其中，“＋”为取正函数$$\begin{array}{r}{\left[z\right]}_{+}=\{\begin{array}{rl}& z,z>0\\ & 0,z\le 0\end{array}\end{array}$$

3、非线性支持向量机与核函数

核函数

设$\mathcal{X}$是输入空间（欧氏空间$R^n$的子集或离散集合），$\mathcal{H}$是特征空间（希尔伯特空间），如果存在一个从$\mathcal{X}$到$\mathcal{H}$的映射$$\begin{array}{rl}& \varphi \left(x\right):\mathcal{X}\to \mathcal{H}\end{array}$$

使得对所有$x,z\in \mathcal{X}$，函数$K\left(x,z\right)$满足条件
$$\begin{array}{rl}& K\left(x,z\right)=\varphi \left(x\right)\cdot \varphi \left(z\right)\end{array}$$

则称$K\left(x,z\right)$为核函数，$\varphi \left(x\right)$为映射函数，式中$\varphi \left(x\right)\cdot \varphi \left(z\right)$为$\varphi \left(x\right)$和$\varphi \left(z\right)$的内积。

常用核函数

多项式核函数$$\begin{array}{rl}& K\left(x,z\right)={\left(x\cdot z+1\right)}^p\end{array}$$

高斯核函数
$$\begin{array}{rl}& K\left(x,z\right)=\exp \left(-\frac{\Vert x-z{\Vert }^2}{2{\sigma }^2}\right)\end{array}$$

非线性支持向量分类机

非线性支持向量机：从非线性分类训练集，通过核函数与软间隔最大化，学习得到分类决策函数
$$\begin{array}{rl}& f\left(x\right)=sign\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K\left(x,x_i\right)+b^{\ast }\right)\end{array}$$

称为非线性支持向量机，$K\left(x,z\right)$是正定核函数。

非线性支持向量机学习算法：

• 输入：训练数据集$T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$，其中$x_i\in \mathcal{X}=R^n,y_i\in \mathcal{Y}=\left\{+1,-1\right\},i=1,2,\cdots ,N$
• 输出：分类决策函数

1. 选择适当的核函数$K\left(x,z\right)$和惩罚参数$C\ge 0$，构建并求解约束最优化问题$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i,x_j\right)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,\cdots ,N\end{array}$$
   求得最优解$${\alpha }^{\ast }=\left({\alpha }_1^{\ast },{\alpha }_1^{\ast },\cdots ,{\alpha }_N^{\ast }\right)$$
2. 计算$$\begin{array}{rl}& \\ & w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\end{array}$$
   并选择${\alpha }^{\ast }$的一个分量$0<{\alpha }_j^{\ast }<C$，计算$$\begin{array}{rl}& \\ & b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K\left(x_i,x_j\right)\end{array}$$
3. 得到分离超平面$$\begin{array}{rl}& \\ & w^{\ast }\cdot x+b^{\ast }=0\end{array}$$
   以及分类决策函数
   $$\begin{array}{rl}& \\ & f\left(x\right)=sign\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K\left(x_i,x_j\right)+b^{\ast }\right)\end{array}$$

4、序列最小最优化算法

本节讨论支持向量机学习的实现问题。我们知道，支持向量机的学习问题可以形式化为求解凸二次规划问题。这样的凸二次规划问题具有全局最优解，并且有许多最优化算法可以用于这一问题的求解。但是当训练样本容量很大时，这些算法往往变得非常低效，以致无法使用。

两个变量二次规划的求解方法

序列最小最优化（sequential minimal optimization，SMO）算法 要解如下凸二次规划的对偶问题：
$$\begin{array}{rl}\underset{\alpha }{\min }& \frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i,x_j\right)-\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,\cdots ,N\end{array}$$

选择${\alpha }_1,{\alpha }_2$两个变量，其他变量${\alpha }_i\left(i=3,4,\cdots ,N\right)$是固定的，SMO的最优化问题的子问题
$$\begin{array}{rl}& \underset{{\alpha }_1,{\alpha }_2}{\min }W\left({\alpha }_1,{\alpha }_2\right)=\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2\\ & -\left({\alpha }_1+{\alpha }_2\right)+y_1{\alpha }_1\sum _{i=3}^N{y}_i{\alpha }_i\\ & \\ & \end{array}$$