逆波兰式是什么？

1. 逆波兰式是什么？

逆波兰式，也称逆波兰记法（Reverse Polish Notation，缩写为RPN），是一种在数学和计算机科学中用于表示算术表达式的方法。它的特点是操作符在操作数的后面，不需要括号来改变运算的优先级。

举个例子，我们通常写出的算术表达式是“2 + 3”。在逆波兰记法中，这个表达式会被写作“2 3 +”。

逆波兰记法的一个主要优点是它可以消除表达式中的括号，并使得运算的执行顺序更加明确。在计算机科学中，逆波兰记法可以更简单高效地进行表达式的求值。例如，使用栈数据结构，可以轻松地计算逆波兰表达式。

逆波兰记法得名于波兰逻辑学家扬·卢卡谢维奇（Jan Łukasiewicz）。虽然他原创的“波兰记法”将操作符放在操作数之前（如“+ 2 3”），但“逆波兰记法”将操作符放在操作数之后，这使得它在实际中更容易使用，特别是在计算机科学领域。

我们来看一些逆波兰记法（Reverse Polish Notation, RPN）的例子。以下是一些常见的算术表达式以及他们对应的逆波兰表示形式：

常规表达式：(7 - 4) * 2，对应的RPN表示：7 4 - 2 *

解释：先从7中减去4，然后将结果乘以2。

常规表达式：5 + ((1 + 2) * 4) - 3，对应的RPN表示：5 1 2 + 4 * + 3 -

解释：先进行1+2，然后将结果乘以4，接着与5相加，最后从中减去3。

常规表达式：(3 + 4) * (5 * 6)，对应的RPN表示：3 4 + 5 6 * *

解释：先进行3+4，同时进行5*6，然后将两个结果相乘。

2. 按照逆波兰式进行计算

这是一个使用Java实现的逆波兰式（RPN）计算器的简单示例。该计算器可以处理包含四种基本算术运算的RPN表达式。

import java.util.Stack;
 
public class RPNCalculator {
    public static int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();
 
        for (String token : tokens) {
            switch (token) {
                case "+":   //但是符号时，就进行运算
                    stack.push(stack.pop() + stack.pop());    //取出当前栈里面的2个元素，进行运算后，再push进去
                    break;
 
                case "-":
                    stack.push(-stack.pop() + stack.pop());
                    break;
 
                case "*":
                    stack.push(stack.pop() * stack.pop());
                    break;
 
                case "/":
                    int n1 = stack.pop(), n2 = stack.pop();
                    stack.push(n2 / n1);
                    break;
 
                default: // 如果是普通字符，则直接入栈
                    stack.push(Integer.parseInt(token));
            }
        }
 
        return stack.pop();
    }
 
    public static void main(String[] args) {
        String[] rpnExpression = {"2", "1", "+", "3", "*"};
        System.out.println(evalRPN(rpnExpression));
    }
}

在这个例子中，evalRPN函数接受一个字符串数组，每个字符串表示RPN表达式中的一个元素（一个数字或一个操作符）。然后，它使用一个栈来存储和操作数字。

对于每个元素，它检查是否是一个操作符（“+”、“-”、“*” 或 “/”）。如果是，它就从栈中弹出两个元素，执行相应的操作，然后将结果推回到栈中。如果元素是一个数字，它就将其推到栈中。

在处理所有元素后，栈顶的元素就是表达式的结果。

在main函数中，我们创建了一个逆波兰表达式字符串数组{“2”, “1”, “+”, “3”, “*”}，这个表达式等同于常规表达式（2+1）*3，然后我们调用evalRPN函数计算它。计算结果将会打印出来。

以3+4为例，进行解析，对应的波兰形式是 3 4 +：
1）按照波兰形式，压入栈

2）压完后，从上向下，取出栈中的元素，一般顶层一定是一个运算符
当从栈中取出运算符号后，会接着把下面的2个元素取出，然后运算，再压入栈
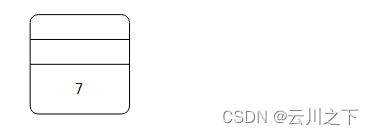
取出+号后， 取出 4 ，再取出3，进行运算，得到7，然后压入栈

此时栈的状态：

3） 继续把后续的波兰式压入栈，依次压入5、6、*号

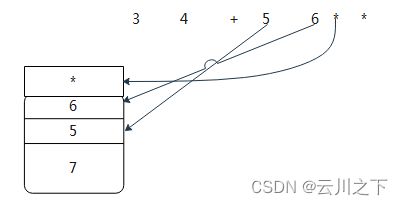
4）
继续把后续的波兰式压入栈，依次压入5、6、*号

当栈的顶层是符号时，又要进行运算，取出下面的2个元素，进行运算

5*6=30，把30压入栈

此时栈的状态：

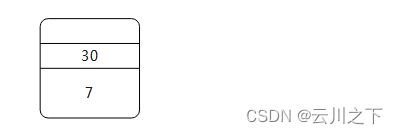
5）继续压入波兰式中的内容 ，是最后一个*号

30*7 + 210

3. 如何转化普通表达式为逆波兰形式

(3 + 4) * (5 * 6) 是如何转为 3 4 + 5 6 * * 的 ？

我们知道 A + B 需要被整理为： A B + 那么对于复杂公式，同样如此，我们可以把A看做是一个 (3+4)的表达式，这样就好理解了。

那么(3 + 4) * (5 * 6) 进行处理的顺序：
1） 先把大的模块进行转换 (3 + 4) (5 * 6) *
1） 把步骤1中的 3 + 4 替换为 3 4 +
2） 把步骤1中的 5 * 6 替换为 5 6 *
3） 得到最后的 3 4 + 5 6 * *

注意：上面的是代数思想，不是计算机的处理方式，如过想写个程序进行计算，那么需要从左至右进行处理，基本原理和RPNCalculator 类似，只不过是反着写

参考

逆波兰式是什么？