像素坐标系、图像坐标系、相机坐标系之间的转换

前言

这些确实很重要
但是因为个人原因，本文对相机坐标系转换到世界坐标系不作记录

正文

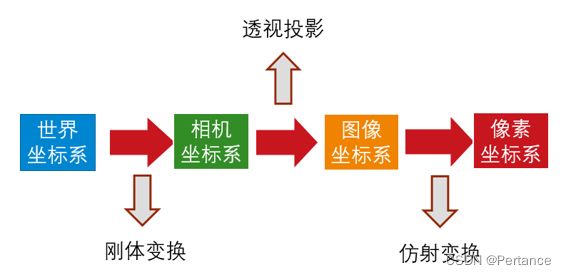
像素坐标系，图像坐标系，相机坐标系，世界坐标系这四个关键坐标系的转换流程如下

通过针孔摄像机模型把三维世界的点映射到二维空间的示意图大概长这样

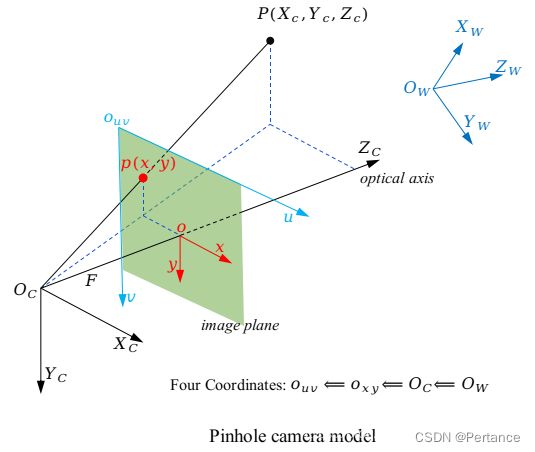
$u,v$表示像素坐标。$x,y$表示图像坐标。$X_C,Y_C,Z_C$表示相机坐标，$O_C$表示相机坐标系的原点。$X_W,Y_W,Z_W$表示世界坐标

如果抛掉世界坐标系和相机坐标系，像素坐标$(u,v)$到图像坐标$(x,y)$的仿射变换很简单

[ u v 1 ] \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} ​uv1​ ​= [ 1 / d x 0 u 0 0 1 / d y v 0 0 0 1 ] \begin{bmatrix} 1/dx & 0 & u_0 \\ 0 & 1/dy & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} ​1/dx00​01/dy0​u0​v0​1​ ​ [ x y 1 ] \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} ​xy1​ ​

首先明确像素到图像之间的转换不仅是数值，也包含了单位的转换，即像素/px到毫米/mm，这样更容易理解公式，其中$dx$和$dy$分别代表$x$方向和$y$方向上单个像素对应的长度，$u_0$和$v_0$分别代表主点的像素坐标（相机光轴与成像平面的交点），换个皮肤就长下面这样

$\{\begin{array}{l}x=(u-u_0)\ast dx\\ y=(v-v_0)\ast dy\end{array}$

结合图一起看就会发现，先把像素点移到主点位置，然后用像素个数乘单个像素对应的长度就是图像坐标

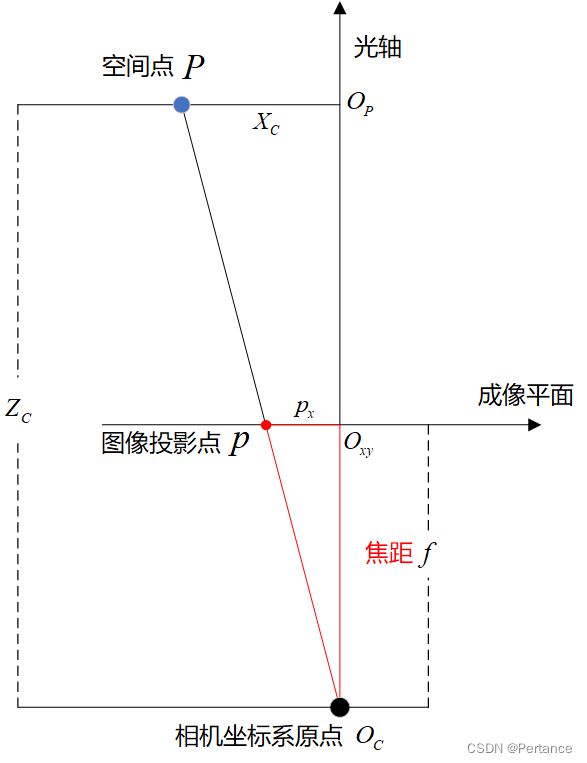
现在把相机坐标系加上，稍稍复杂了一点，简单地把透视投影的部分理解成相似三角形，想象你平行于相机坐标系Z轴，朝向Y轴正方向把整个坐标系拍在墙上，然后就有了下图

从图中很容易看出，三角形$O_C{O}_{xy}p$与三角形$O_C{O}_{P}P$相似，补充设定如下
线段 $p{O}_{xy}=p_x$ 这里的$p_x$就是点$p$的$x$坐标值
线段 $O_C{O}_{xy}=f$ 这里的$f$就是焦距
线段 $O_C{O}_P=Z_C$ 这里的$Z_C$就是$P$点的相机坐标$Z_C$
线段 $P{O}_P=X_C$ 这里的$X_C$就是$P$点的相机坐标$X_C$
从图中得出关系：$X_C/Z_C=p_x/f$
类似地，换个方向拍坐标系得出另一个关系，$Y_C/Z_C=p_y/f$
整理方程如下

$\{\begin{array}{l}{X}_C/Z_C=x/f\\ Y_C/Z_C=y/f\\ Z_C=Z_C\end{array}$

换一下皮肤

$\{\begin{array}{l}{Z}_C\ast x=f\ast X_C\\ Z_C\ast y=f\ast Y_C\\ Z_C\ast 1=1\ast Z_C\end{array}$

提取$Z_C$，推出如下关系

Z C [ x y 1 ] Z_C\begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} ZC​ ​xy1​ ​= [ f 0 0 0 f 0 0 0 1 ] \begin{bmatrix} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} ​f00​0f0​001​ ​ [ X C Y C Z C ] \begin{bmatrix} X_C \\ Y_C \\ Z_C \\ \end{bmatrix} ​XC​YC​ZC​​ ​

再结合像素坐标转图像坐标推出如下(忘记了就回头看看)

Z C [ u v 1 ] Z_C\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} ZC​ ​uv1​ ​= [ 1 / d x 0 u 0 0 1 / d y v 0 0 0 1 ] \begin{bmatrix} 1/dx & 0 & u_0 \\ 0 & 1/dy & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} ​1/dx00​01/dy0​u0​v0​1​ ​ [ f 0 0 0 f 0 0 0 1 ] \begin{bmatrix} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} ​f00​0f0​001​ ​ [ X C Y C Z C ] \begin{bmatrix} X_C \\ Y_C \\ Z_C \\ \end{bmatrix} ​XC​YC​ZC​​ ​

一般相机内参的表示形式如下

[ f x 0 u 0 0 f y v 0 0 0 1 ] \begin{bmatrix} f_x & 0 & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} ​fx​00​0fy​0​u0​v0​1​ ​= [ f / d x 0 u 0 0 f / d y v 0 0 0 1 ] \begin{bmatrix} f/d_x & 0 & u_0 \\ 0 & f/d_y & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} ​f/dx​00​0f/dy​0​u0​v0​1​ ​

最终形态如下

Z C [ u v 1 ] Z_C\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} ZC​ ​uv1​ ​= [ f x 0 u 0 0 f y v 0 0 0 1 ] \begin{bmatrix} f_x & 0 & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} ​fx​00​0fy​0​u0​v0​1​ ​ [ X C Y C Z C ] \begin{bmatrix} X_C \\ Y_C \\ Z_C \\ \end{bmatrix} ​XC​YC​ZC​​ ​

到此为止，可以得到方程如下

$\{\begin{array}{l}u=f_X\ast X_C/Z_C+u_0\\ v=f_y\ast Y_C/Z_C+v_0\\ Z_C=Z_C\end{array}$

再换个皮肤就更清晰了

$\{\begin{array}{l}{X}_C=(u-u_0)\ast Z_C/f_x\\ Y_C=(v-v_0)\ast Z_C/f_y\\ Z_C=Z_C\end{array}$

很容易发现的是，需要的参数$f_x,f_y,u_0,v_0$就是相机内参提供的4个值。
具体求相机内参的方法本文不作介绍，张正友标定法永远滴神

已知像素坐标$u,v$，想要求解相机坐标$X_C,Y_C,Z_C$，还需要知道的最后一个关键参数就是$Z_C$

$Z_C$可以通过深度相机获取(包括但不限于双目、双目结构光、单目结构光等相机)，普通的工业相机还可以借助PnP求解法，本文不多作介绍