代码随想录算法训练营第十一天 | 二叉树系列2

101 对称二叉树

直接阅读的代码随想录的解答。

该用哪种遍历顺序？这很重要

本题遍历只能是“后序遍历”，因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
正是因为要遍历两棵树而且要比较内侧和外侧节点，所以准确的来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。
但都可以理解算是后序遍历，尽管已经不是严格上在一个树上进行遍历的后序遍历了。其实后序也可以理解为是一种回溯，当然这是题外话，讲回溯的时候会重点讲的。

三种方法，递归，迭代队列，迭代栈。

难点在于递归终止条件的判断。

迭代法要注意：

在迭代法中使用了队列，需要注意的是这不是层序遍历，而且仅仅通过一个容器来成对的存放我们要比较的元素，知道这一本质之后就发现，用队列，用栈，甚至用数组，都是可以的。

二叉树很重要的一点：确定遍历顺序

需要收集孩子的信息，向上一层返回的题，要用后序遍历，左右中。

关于递归

这里写递归时可以发现，只要一个子递归函数返回了False，那么最终结果一定为False，没必要执行剩下的递归，但是递归函数中的return是无法做到强制跳出了，搜了一下，使用抛出异常的方式，跳出。

如果是Python语言，搜索了一下，网上给出的方法是：使用一个布尔型的全局变量。

代码随想录的代码

递归：

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        return self.compare(root.left, root.right)
        
    def compare(self, left, right):
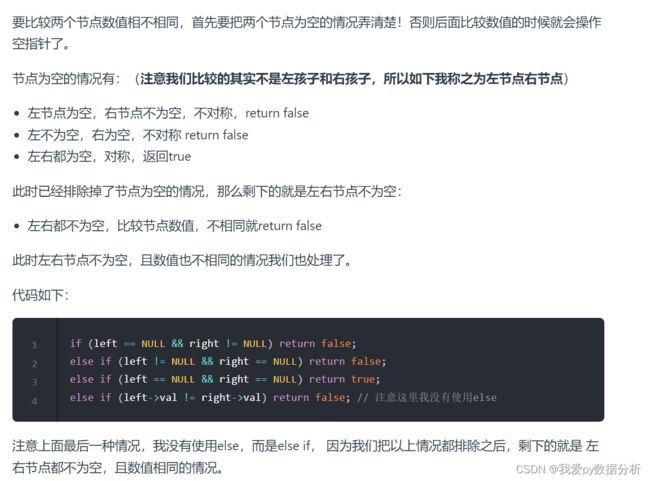
        #首先排除空节点的情况
        if left == None and right != None: return False
        elif left != None and right == None: return False
        elif left == None and right == None: return True
        #排除了空节点，再排除数值不相同的情况
        elif left.val != right.val: return False
        
        #此时就是：左右节点都不为空，且数值相同的情况
        #此时才做递归，做下一层的判断
        outside = self.compare(left.left, right.right) #左子树：左、 右子树：右
        inside = self.compare(left.right, right.left) #左子树：右、 右子树：左
        isSame = outside and inside #左子树：中、 右子树：中 （逻辑处理）
        return isSame

迭代法：使用队列

import collections
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        queue = collections.deque()
        queue.append(root.left) #将左子树头结点加入队列
        queue.append(root.right) #将右子树头结点加入队列
        while queue: #接下来就要判断这这两个树是否相互翻转
            leftNode = queue.popleft()
            rightNode = queue.popleft()
            if not leftNode and not rightNode: #左节点为空、右节点为空，此时说明是对称的
                continue
            
            #左右一个节点不为空，或者都不为空但数值不相同，返回false
            if not leftNode or not rightNode or leftNode.val != rightNode.val:
                return False
            queue.append(leftNode.left) #加入左节点左孩子
            queue.append(rightNode.right) #加入右节点右孩子
            queue.append(leftNode.right) #加入左节点右孩子
            queue.append(rightNode.left) #加入右节点左孩子
        return True

迭代法：使用栈

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        st = [] #这里改成了栈
        st.append(root.left)
        st.append(root.right)
        while st:
            rightNode = st.pop()
            leftNode = st.pop()
            if not leftNode and not rightNode:
                continue
            if not leftNode or not rightNode or leftNode.val != rightNode.val:
                return False
            st.append(leftNode.left)
            st.append(rightNode.right)
            st.append(leftNode.right)
            st.append(rightNode.left)
        return True

层次遍历：

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        
        queue = collections.deque([root.left, root.right])
        
        while queue:
            level_size = len(queue)
            
            if level_size % 2 != 0:
                return False
            
            level_vals = []
            for i in range(level_size):
                node = queue.popleft()
                if node:
                    level_vals.append(node.val)
                    queue.append(node.left)
                    queue.append(node.right)
                else:
                    level_vals.append(None)
                    
            if level_vals != level_vals[::-1]:
                return False
            
        return True

我的代码(理解后编写)

递归：明确三部曲即可。

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if root == None :
            return True
        return self.isequal(root.left,root.right)



    def isequal(self,left,right):
        if left == None and right == None :
            return True
        elif left != None and right == None :
            return False
        elif left == None and right != None :
            return False
        elif left.val != right.val :
            return False
        else :
            isleft = self.isequal(left.left,right.right)
            isright = self.isequal(left.right,right.left)
            return isleft and isright

递归(强制退出，无法运行的错误代码)：似乎不需要了解这种情况了

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if root == None :
            return True
        
        global judge
        judge=True
        self.isequal(root.left,root.right,judge)
        return judge



    def isequal(self,left,right,judge):
        if judge :
            if left == None and right == None :
                return True
            elif left != None and right == None :
                judge = False
                return False
            elif left == None and right != None :
                judge = False
                return False
            elif left.val != right.val :
                judge = False
                return False
            else :
                isleft = self.isequal(left.left,right.right,judge)
                isright = self.isequal(left.right,right.left,judge)
                return isleft and isright
        else :
            return False

递归(强制退出，用self定义了类内的全局变量)

class Solution:

    def __init__(self):
        self.judge = True

    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if root == None :
            return True
        
        
        self.isequal(root.left,root.right,self.judge)
        return self.judge



    def isequal(self,left,right,judge):
        if self.judge :
            if left == None and right == None :
                return True
            elif left != None and right == None :
                self.judge = False
                return False
            elif left == None and right != None :
                self.judge = False
                return False
            elif left.val != right.val :
                self.judge = False
                return False
            else :
                isleft = self.isequal(left.left,right.right,judge)
                isright = self.isequal(left.right,right.left,judge)
                self.judge = isleft and isright
                return self.judge
        else :
            return False

迭代法：使用队列
编写要点：在此队列中，None是要加入队列的，如果left和right均为None，就continue。

from collections import deque
class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if root == None :
            return True

        dq = deque()
        dq.append(root.left)
        dq.append(root.right)
        while dq :
            left = dq.popleft()
            right = dq.popleft()
            if left == None and right == None :
                continue
            elif left != None and right == None : 
                return False
            elif left == None and right != None :
                return False
            elif left.val != right.val :
                return False
            else :
                dq.append(left.left)
                dq.append(right.right)
                dq.append(left.right)
                dq.append(right.left)
        return True

迭代法：使用栈

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if root == None :
            return True

        st = []
        st.append(root.left)
        st.append(root.right)
        while st :
            left = st.pop()
            right = st.pop()
            if left == None and right == None :
                continue
            elif left != None and right == None : 
                return False
            elif left == None and right != None :
                return False
            elif left.val != right.val :
                return False
            else :
                st.append(left.left)
                st.append(right.right)
                st.append(left.right)
                st.append(right.left)
        return True

层次遍历，用deque

from collections import deque
class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if root == None :
            return True
        stack = deque()
        stack.append(root.left)
        stack.append(root.right)
        while stack :
            size = len(stack)
            if size % 2 != 0:
               return False
            res = []
            for i in range(size):
                node = stack.popleft()
                if node :
                    res.append(node.val)
                    stack.append(node.left)
                    stack.append(node.right)
                else :
                    res.append(None)
            if res != res[::-1] :
                return False

        return True

100 相同的树

我的代码

一刷只写了递归法，其他方法二刷再写

class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        if p == None and q == None :
            return True
        elif p != None and q == None:
            return False
        elif p == None and q != None:
            return False
        elif p.val != q.val :
            return False
        else :
            left = self.isSameTree(p.left,q.left)
            right = self.isSameTree(p.right,q.right)
            return left and right

572 另一个树的子树

我的代码

一刷虽然通过了，但方法是层次遍历+递归相等树判断，去遍历每一个节点，代码显得冗余

from collections import deque
class Solution:
    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        if root == None and subRoot == None :
            return True
        elif root != None and subRoot == None:
            return False
        elif root == None and subRoot != None:
            return False
        else :
            dq = deque()
            dq.append(root)
            while dq:
                size = len(dq)
                for i in range(size):
                    node = dq.popleft()
                    if node :
                        judge = self.isSameTree(node,subRoot)
                        if judge :
                            return True
                        dq.append(node.left)
                        dq.append(node.right)
            return False
                        

    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        if p == None and q == None :
            return True
        elif p != None and q == None:
            return False
        elif p == None and q != None:
            return False
        elif p.val != q.val :
            return False
        else :
            left = self.isSameTree(p.left,q.left)
            right = self.isSameTree(p.right,q.right)
            return left and right

录友的代码，只用递归！！！

一个树是另一个树的子树，则：要么这两个树相等；要么这个树是左树的子树；要么这个树hi右树的子树

又因为提议可知，子树不为None，所以递归的判断环节可以简化。

但是这样只用递归，在时间消耗上比我的层次遍历稍高。

class Solution:
    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:  
        if root == None :
            return False
        else :
            jg1 = self.isSameTree(root,subRoot)
            jg2 = self.isSubtree(root.left,subRoot)
            jg3 = self.isSubtree(root.right,subRoot)
            return jg1 or jg2 or jg3
                

    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        if p == None and q == None :
            return True
        elif p != None and q == None:
            return False
        elif p == None and q != None:
            return False
        elif p.val != q.val :
            return False
        else :
            left = self.isSameTree(p.left,q.left)
            right = self.isSameTree(p.right,q.right)
            return left and right

104 二叉树的最大深度

用层次遍历的方法，是层次遍历的模板题，这里只学习使用递归的方法。

重点

搞清楚，深度和高度的区别。

高度：从上到下，3 2 1 。深度：从上到下：1 2 3 。

求高度，从下向上计数，为后序遍历，左右中，有一个中，就加一。求深度，从上向下计数，为前序遍历，中左右，有一个中，就加一。

根节点的高度，就是这颗二叉树的最大深度。

代码随想录的代码

后序遍历：（求高度）

class solution:
    def maxdepth(self, root: treenode) -> int:
        return self.getdepth(root)
        
    def getdepth(self, node):
        if not node:
            return 0
        leftheight = self.getdepth(node.left) #左
        rightheight = self.getdepth(node.right) #右
        height = 1 + max(leftheight, rightheight) #中
        return height

前序遍历：（求深度）
不推荐，不学习。二刷时再说。放一个Java的代码，着重看回溯的过程。

class Solution {
public:
    int result;
    void getDepth(TreeNode* node, int depth) {
        result = depth > result ? depth : result; // 中

        if (node->left == NULL && node->right == NULL) return ;

        if (node->left) { // 左
            depth++;    // 深度+1
            getDepth(node->left, depth);
            depth--;    // 回溯，深度-1
        }
        if (node->right) { // 右
            depth++;    // 深度+1
            getDepth(node->right, depth);
            depth--;    // 回溯，深度-1
        }
        return ;
    }
    int maxDepth(TreeNode* root) {
        result = 0;
        if (root == 0) return result;
        getDepth(root, 1);
        return result;
    }
};

我的代码(理解后自己写)

后序遍历：（求高度）

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root == None :
            return 0
        left = self. maxDepth(root.left)
        right = self. maxDepth(root.right)
        return 1+max(left,right)

前序遍历：（求深度）
不推荐，不学习。二刷时再说。

559 N 叉树的最大深度

后序遍历，根节点的高度就是最大深度。

代码随想录的代码

class Solution:
    def maxDepth(self, root: 'Node') -> int:
        if not root:
            return 0
        
        max_depth = 1
        
        for child in root.children:
            max_depth = max(max_depth, self.maxDepth(child) + 1)
        
        return max_depth

我的代码

class Solution:
    def maxDepth(self, root: 'Node') -> int:
        if root == None :
            return 0
        res = []
        n = len(root.children)
        if n==0 :
            return 1
        else :
            for i in root.children :
                res.append(self.maxDepth(i))
            
            depth = 1 + max(res)
            return depth

111 二叉树的最小深度

用层次遍历的方法，是层次遍历的模板题，这里只学习使用递归的方法。

同样使用后续遍历。

此题一定要注意最小深度的定义，是叶子节点到根节点的最短距离，而叶子节点的定义为：左右孩子均为None 。

很容易错的一道题，没弄明白之前，递归逻辑也不好写。

注意避开陷阱！当只有一个孩子为None时，返回的是 1+不为空子树的最小高度。

代码随想录的代码

后序+递归：

class Solution:
    def getDepth(self, node):
        if node is None:
            return 0
        leftDepth = self.getDepth(node.left)  # 左
        rightDepth = self.getDepth(node.right)  # 右
        
        # 当一个左子树为空，右不为空，这时并不是最低点
        if node.left is None and node.right is not None:
            return 1 + rightDepth
        
        # 当一个右子树为空，左不为空，这时并不是最低点
        if node.left is not None and node.right is None:
            return 1 + leftDepth
        
        result = 1 + min(leftDepth, rightDepth)
        return result

    def minDepth(self, root):
        return self.getDepth(root)

前序+递归：这里用 init 定义一个self的全局变量的思路，很值得学习。隐藏了回溯的思想，每次递归时，并未改变depth。

class Solution:
    def __init__(self):
        self.result = float('inf')

    def getDepth(self, node, depth):
        if node is None:
            return
        if node.left is None and node.right is None:
            self.result = min(self.result, depth)
        if node.left:
            self.getDepth(node.left, depth + 1)
        if node.right:
            self.getDepth(node.right, depth + 1)

    def minDepth(self, root):
        if root is None:
            return 0
        self.getDepth(root, 1)
        return self.result

二刷要着重自己独立编写

这里写的就不如代码随想录给出的标准答案，调用递归次数过多，就应该在第一个 if 判断后，就去统计左右深度。

class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        if root == None :
            return 0
        
        if root.left == None and root.right == None :
            return 1
        elif root.left == None :
            return 1 + self.minDepth(root.right)
        elif root.right == None :
            return 1 + self.minDepth(root.left)
        else :
            return 1 + min(self.minDepth(root.left),self.minDepth(root.right))

222 完全二叉树的节点个数

迭代法依然是层序遍历的蓝本。递归法也好理解，递归的目标是左右子树的节点个数。值得学习的是，利用完全二叉树的性质，来写出时间复杂度更低的代码。

递归，依然是后序遍历，本质上和其高度类似，只不过递归逻辑由求高度，变为了求数量。

代码随想录的代码

递归：

class Solution:
    def countNodes(self, root: TreeNode) -> int:
        return self.getNodesNum(root)
        
    def getNodesNum(self, cur):
        if not cur:
            return 0
        leftNum = self.getNodesNum(cur.left) #左
        rightNum = self.getNodesNum(cur.right) #右
        treeNum = leftNum + rightNum + 1 #中
        return treeNum

利用完全二叉树：

class Solution:
    def countNodes(self, root: TreeNode) -> int:
        if not root:
            return 0
        left = root.left
        right = root.right
        leftDepth = 0 #这里初始为0是有目的的，为了下面求指数方便
        rightDepth = 0
        while left: #求左子树深度
            left = left.left
            leftDepth += 1
        while right: #求右子树深度
            right = right.right
            rightDepth += 1
        if leftDepth == rightDepth:
            return (2 << leftDepth) - 1 #注意(2<<1) 相当于2^2，所以leftDepth初始为0
        return self.countNodes(root.left) + self.countNodes(root.right) + 1

二刷要着重自己独立编写

利用完全二叉树：

class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        if root == None :
            return 0
        leftnode =  root.left
        rightnode = root.right
        ln = 1
        rn = 1
        while leftnode :
            leftnode = leftnode.left
            ln += 1
        while rightnode :
            rightnode = rightnode.right
            rn += 1
        if ln == rn :
            return 2**ln - 1
        else :
            return 1+self.countNodes(root.left)+self.countNodes(root.right)

110 平衡二叉树

使用递归的思想编写，不用迭代方法，首先此题不能用层序遍历，迭代法无法很好地模拟回溯过程，中间存在很多重复计算。

具体分析参考代码随想录的文章即可。
平衡二叉树

我的代码

发现，我现在写递归，很喜欢加一个全局变量来做判断了，也不知道是好是坏。

所以还是学习一下的代码随想录的解答方式。

class Solution:

    def __init__(self):
        self.judge = True

    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        self.digui(root)
        return self.judge

    def digui(self,root):
        if root == None :
            return 0
        if self.judge :
            left = self.digui(root.left)
            right = self.digui(root.right)
            if abs(left-right) > 1 :
                self.judge = False
            return 1 + max(left,right)
        else :
            return 0
        

代码随想录的代码

其实对递归了解较深之后，这样一层一层返回-1，和搞一个self变量是一样的效果！！！

所以还是学习下面这种写法吧。

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        if self.get_height(root) != -1:
            return True
        else:
            return False

    def get_height(self, root: TreeNode) -> int:
        # Base Case
        if not root:
            return 0
        # 左
        if (left_height := self.get_height(root.left)) == -1:
            return -1
        # 右
        if (right_height := self.get_height(root.right)) == -1:
            return -1
        # 中
        if abs(left_height - right_height) > 1:
            return -1
        else:
            return 1 + max(left_height, right_height)

257 二叉树的所有路径

第一道，递归+回溯的题目！！！

回溯一直是没有掌握的点！！！

直接学习代码随想录的解答。文章链接如下。
二叉树的所有路径

重点

同样需要先确定遍历顺序，肯定为前序遍历，因为输出路径为父节点指向子节点，中序和后序，无法得到父节点到子节点的指向。

所谓隐藏回溯，就是对Path做拷贝操作，这样在后序递归时，对Path的修改，不会影响到上一层的其他带Path的语句，所以不需要回溯操作。

对于Python来说，对同一个变量进行操作，所有的地方都会发生改变，类似于C语言中对地址的操作，想要不改变原变量，就要用copy()操作。

代码随想录的代码

递归法+回溯

class Solution:
    def traversal(self, cur, path, result):
        path.append(cur.val)  # 中
        if not cur.left and not cur.right:  # 到达叶子节点
            sPath = '->'.join(map(str, path))
            result.append(sPath)
            return
        if cur.left:  # 左
            self.traversal(cur.left, path, result)
            path.pop()  # 回溯
        if cur.right:  # 右
            self.traversal(cur.right, path, result)
            path.pop()  # 回溯

    def binaryTreePaths(self, root):
        result = []
        path = []
        if not root:
            return result
        self.traversal(root, path, result)
        return result

递归法+隐形回溯（版本一）

from typing import List, Optional

class Solution:
    def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
        if not root:
            return []
        result = []
        self.traversal(root, [], result)
        return result
    
    def traversal(self, cur: TreeNode, path: List[int], result: List[str]) -> None:
        if not cur:
            return
        path.append(cur.val)
        if not cur.left and not cur.right:
            result.append('->'.join(map(str, path)))
        if cur.left:
            self.traversal(cur.left, path[:], result)
        if cur.right:
            self.traversal(cur.right, path[:], result)

递归法+隐形回溯（版本二）

class Solution:
    def binaryTreePaths(self, root: TreeNode) -> List[str]:
        path = ''
        result = []
        if not root: return result
        self.traversal(root, path, result)
        return result
    
    def traversal(self, cur: TreeNode, path: str, result: List[str]) -> None:
        path += str(cur.val)
        # 若当前节点为leave，直接输出
        if not cur.left and not cur.right:
            result.append(path)

        if cur.left:
            # + '->' 是隐藏回溯
            self.traversal(cur.left, path + '->', result)
        
        if cur.right:
            self.traversal(cur.right, path + '->', result)

迭代法(有些难理解的)

class Solution:

    def binaryTreePaths(self, root: TreeNode) -> List[str]:
        # 题目中节点数至少为1
        stack, path_st, result = [root], [str(root.val)], []

        while stack:
            cur = stack.pop()
            path = path_st.pop()
            # 如果当前节点为叶子节点，添加路径到结果中
            if not (cur.left or cur.right):
                result.append(path)
            if cur.right:
                stack.append(cur.right)
                path_st.append(path + '->' + str(cur.right.val))
            if cur.left:
                stack.append(cur.left)
                path_st.append(path + '->' + str(cur.left.val))

        return result

此题很难，二刷时要注意

二刷要着重自己独立编写

递归法+回溯

class Solution:
    def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
        if root == None :
            return None
        res = []
        path = []
        self.digui(root,path,res)
        return res

    def digui(self,cur,path,res):
        path.append(cur.val)
        if cur.left == None and cur.right == None :
            sPath = '->'.join(map(str, path))
            res.append(sPath)
            return 
        if cur.left :
            self.digui(cur.left,path,res)
            path.pop()
        if cur.right :
            self.digui(cur.right,path,res)
            path.pop()

二叉树系列2总结

直接放代码随想录总结文章的链接。
二叉树系列2总结

回溯法其实就是递归，但是很少人用迭代的方式去实现回溯算法！

讲了这么多二叉树题目的迭代法，有的同学会疑惑，迭代法中究竟什么时候用队列，什么时候用栈？

如果是模拟前中后序遍历就用栈，如果是适合层序遍历就用队列，当然还是其他情况，那么就是 先用队列试试行不行，不行就用栈